Rabi problem
Encyclopedia
The Rabi problem concerns the response of an atom
to an applied harmonic
electric field
, with an applied frequency
very close to the atom's natural frequency. It provides a simple and generally solvable example of light-atom interactions.
with the electric part of the Lorentz force
as the driving term:
,
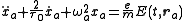where it has been assumed that the atom can be treated as a charged particle (of charge e) oscillating about its equilibrium position around a neutral atom. Here, xa is its instantaneous magnitude of oscillation,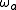
its natural oscillation frequency, and 
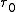its natural lifetime:
,
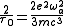which has been calculated based on the dipole
oscillator's energy loss from electromagnetic radiation.
To apply this to the Rabi problem, one assumes that the electric field E is oscillatory in time and constant in space:
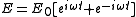
and xa is decomposed into a part ua that is in-phase with the driving E field (corresponding to dispersion), and a part va that is out of phase (corresponding to absorption):
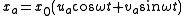
Here, x0 is assumed to be constant, but ua and vaare allowed to vary in time. However, if we assume we are very close to resonance (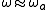
), then these values will be slowly varying in time, and we can make the assumption that 
, 
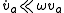and 
, 
.
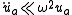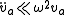With these assumptions, the Lorentz force equations for the in-phase and out-of-phase parts can be rewritten as,
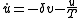
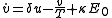
where we have replaced the natural lifetime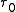
with a more general effective lifetime T (which could include other interactions such as collisions), and have dropped the subscript a in favor of the newly-defined detuning
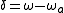, which serves equally well to distinguish atoms of different resonant frequencies. Finally, the constant 
has been defined:
These equations can be solved as follows:
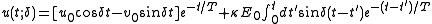
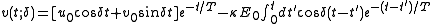
After all transients have died away, the steady state solution takes the simple form,
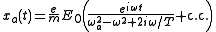
where "c.c." stands for the complex conjugate
of the opposing term.
, spontaneous emission
, and the Bloch-Siegert shift
, a fully quantum mechanical
treatment is necessary.
The simplest approach is through the two-level atom approximation, in which one only treats two energy levels of the atom in question. No atom with only two energy levels exists in reality, but a transition between, for example, two hyperfine states in an atom can be treated, to first approximation, as if only those two levels existed, assuming the drive is not too far off resonance.
The convenience of the two-level atom is that any two-level system evolves in essentially the same way as a spin-1/2 system, in accordance to the optical Bloch equations, which define the dynamics of the pseudo-spin vector in an electric field:
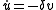
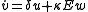
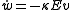
where we have made the rotating wave approximation
in throwing out terms with high angular velocity (and thus small effect on the total spin dynamics over long time periods), and transformed into a set of coordinates rotating at a frequency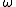
.
There is a clear analogy here between these equations and those that defined the evolution of the in-phase and out-of-phase components of oscillation in the classical case. Now, however, there is a third term w which can be interpreted as the population difference between the excited and ground state (varying from -1 to represent completely in the ground state to +1, completely in the excited state). Keep in mind that for the classical case, there was a continuous energy spectra that the atomic oscillator could occupy, while for the quantum case (as we've assumed) there are only two possible (eigen)states of the problem.
These equations can be also be stated in matrix form:
It is noteworthy that these equations can be written as a vector precession equation:
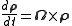
where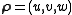
is the pseudo-spin vector and 
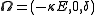acts as an effective torque.
As before, the Rabi problem is solved by assuming the electric field E is oscillatory with constant magnitude E0: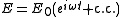
. In this case, the solution can be found by applying two successive rotations to the matrix equation above, of the form
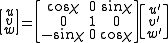
and
where
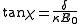
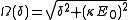
Here, the frequency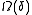
is known as the generalized Rabi frequency, which gives the rate of precession
of the pseudo-spin vector about the transformed u' -axis (given by the first coordinate transformation above). As an example, if the electric field (or laser
) is exactly on resonance (such that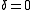
), then the psedo-spin vector will precess about the u axis at a rate of 
. If this (on-resonance) pulse is shone on a collection of atoms originally all in their ground state (w = -1) for a time 
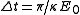, then after the pulse, the atoms will now all be in their excited state (w = 1) because of the 
(or 180 degree) rotation about the u axis. This is known as a 
-pulse, and has the result of a complete inversion.
The general result is given by,
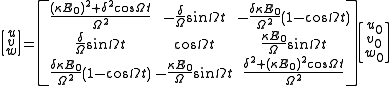
The expression for the inversion w can be greatly simplifed if the atom is assumed to be initially in its ground state (w0 = -1) with u0 = v0 = 0, in which case,
Atom
The atom is a basic unit of matter that consists of a dense central nucleus surrounded by a cloud of negatively charged electrons. The atomic nucleus contains a mix of positively charged protons and electrically neutral neutrons...
to an applied harmonic
Normal mode
A normal mode of an oscillating system is a pattern of motion in which all parts of the system move sinusoidally with the same frequency and with a fixed phase relation. The frequencies of the normal modes of a system are known as its natural frequencies or resonant frequencies...
electric field
Electric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
, with an applied frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
very close to the atom's natural frequency. It provides a simple and generally solvable example of light-atom interactions.
Classical Rabi Problem
In the classical approach, the Rabi problem can be represented by the solution to the driven, damped harmonic oscillatorHarmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
with the electric part of the Lorentz force
Lorentz force
In physics, the Lorentz force is the force on a point charge due to electromagnetic fields. It is given by the following equation in terms of the electric and magnetic fields:...
as the driving term:
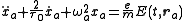,where it has been assumed that the atom can be treated as a charged particle (of charge e) oscillating about its equilibrium position around a neutral atom. Here, xa is its instantaneous magnitude of oscillation,
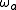its natural oscillation frequency, and 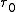its natural lifetime: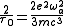,which has been calculated based on the dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
oscillator's energy loss from electromagnetic radiation.
To apply this to the Rabi problem, one assumes that the electric field E is oscillatory in time and constant in space:
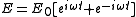
and xa is decomposed into a part ua that is in-phase with the driving E field (corresponding to dispersion), and a part va that is out of phase (corresponding to absorption):
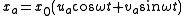
Here, x0 is assumed to be constant, but ua and vaare allowed to vary in time. However, if we assume we are very close to resonance (
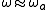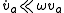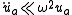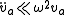), then these values will be slowly varying in time, and we can make the assumption that , and , .With these assumptions, the Lorentz force equations for the in-phase and out-of-phase parts can be rewritten as,
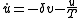
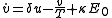
where we have replaced the natural lifetime
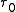with a more general effective lifetime T (which could include other interactions such as collisions), and have dropped the subscript a in favor of the newly-defined detuningLaser detuning
In optical physics, laser detuning is the tuning of a laser to a frequency that is slightly off from a quantum system's resonant frequency. Lasers can be detuned in the lab frame so that they are Doppler shifted to the resonant frequency in a moving system, which allows lasers to affect only...
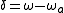, which serves equally well to distinguish atoms of different resonant frequencies. Finally, the constant has been defined:These equations can be solved as follows:
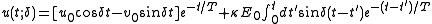
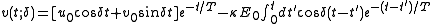
After all transients have died away, the steady state solution takes the simple form,
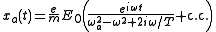
where "c.c." stands for the complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of the opposing term.
Two-level atom
The classical Rabi problem gives some basic results and a simple to understand picture of the issue, but in order to understand phenomena such as inversionPopulation inversion
In physics, specifically statistical mechanics, a population inversion occurs when a system exists in state with more members in an excited state than in lower energy states...
, spontaneous emission
Spontaneous emission
Spontaneous emission is the process by which a light source such as an atom, molecule, nanocrystal or nucleus in an excited state undergoes a transition to a state with a lower energy, e.g., the ground state and emits a photon...
, and the Bloch-Siegert shift
Bloch-Siegert shift
The Bloch-Siegert shift is a phenomenon in quantum physics that becomes important for driven two-level systems when the driving gets strong ....
, a fully quantum mechanical
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
treatment is necessary.
The simplest approach is through the two-level atom approximation, in which one only treats two energy levels of the atom in question. No atom with only two energy levels exists in reality, but a transition between, for example, two hyperfine states in an atom can be treated, to first approximation, as if only those two levels existed, assuming the drive is not too far off resonance.
The convenience of the two-level atom is that any two-level system evolves in essentially the same way as a spin-1/2 system, in accordance to the optical Bloch equations, which define the dynamics of the pseudo-spin vector in an electric field:
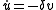
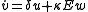
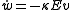
where we have made the rotating wave approximation
Rotating wave approximation
The rotating wave approximation is an approximation used in atom optics and magnetic resonance. In this approximation, terms in a Hamiltonian which oscillate rapidly are neglected. This is a valid approximation when the applied electromagnetic radiation is near resonance with an atomic resonance,...
in throwing out terms with high angular velocity (and thus small effect on the total spin dynamics over long time periods), and transformed into a set of coordinates rotating at a frequency
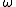.There is a clear analogy here between these equations and those that defined the evolution of the in-phase and out-of-phase components of oscillation in the classical case. Now, however, there is a third term w which can be interpreted as the population difference between the excited and ground state (varying from -1 to represent completely in the ground state to +1, completely in the excited state). Keep in mind that for the classical case, there was a continuous energy spectra that the atomic oscillator could occupy, while for the quantum case (as we've assumed) there are only two possible (eigen)states of the problem.
These equations can be also be stated in matrix form:
It is noteworthy that these equations can be written as a vector precession equation:
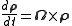
where
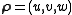is the pseudo-spin vector and 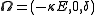acts as an effective torque.As before, the Rabi problem is solved by assuming the electric field E is oscillatory with constant magnitude E0:
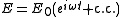. In this case, the solution can be found by applying two successive rotations to the matrix equation above, of the form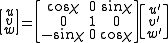and
where
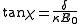
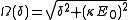
Here, the frequency
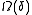is known as the generalized Rabi frequency, which gives the rate of precessionPrecession
Precession is a change in the orientation of the rotation axis of a rotating body. It can be defined as a change in direction of the rotation axis in which the second Euler angle is constant...
of the pseudo-spin vector about the transformed u' -axis (given by the first coordinate transformation above). As an example, if the electric field (or laser
Laser
A laser is a device that emits light through a process of optical amplification based on the stimulated emission of photons. The term "laser" originated as an acronym for Light Amplification by Stimulated Emission of Radiation...
) is exactly on resonance (such that
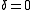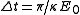), then the psedo-spin vector will precess about the u axis at a rate of . If this (on-resonance) pulse is shone on a collection of atoms originally all in their ground state (w = -1) for a time , then after the pulse, the atoms will now all be in their excited state (w = 1) because of the (or 180 degree) rotation about the u axis. This is known as a -pulse, and has the result of a complete inversion.The general result is given by,
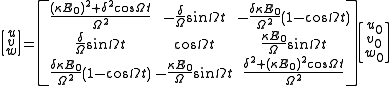
The expression for the inversion w can be greatly simplifed if the atom is assumed to be initially in its ground state (w0 = -1) with u0 = v0 = 0, in which case,
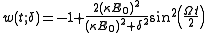
Multimedia
A Java applet that visualizes Rabi Cycles of two-state systems (laser driven):- http://www.itp.tu-berlin.de/menue/lehre/owl/quantenmechanik/zweiniveau/parameter/en/
See also
- Rabi cycleRabi cycleIn physics, the Rabi cycle is the cyclic behaviour of a two-state quantum system in the presence of an oscillatory driving field. A two-state system has two possible states, and if they are not degenerate energy levels the system can become "excited" when it absorbs a quantum of energy.The effect...
- Rabi frequencyRabi frequencyThe Rabi frequency is the frequency of population oscillation for a given atomic transition in a given light field. It is associated with the strength of the coupling between the light and the transition. Rabi flopping between the levels of a 2-level system illuminated with resonant light, will...
- Vacuum Rabi oscillationVacuum Rabi oscillationA vacuum Rabi oscillation is a damped oscillation of an initially excited atom coupled to an electromagnetic resonator or cavity in which the atom alternately emits photon into a single-mode electromagnetic cavity and reabsorbs them. The atom interacts with a single-mode field confined to a limited...
- Jaynes-Cummings modelJaynes-Cummings modelThe Jaynes–Cummings model is a theoretical model in quantum optics. It describes the system of a two-level atom interacting with a quantized mode of an optical cavity, with or without the presence of light...