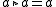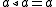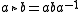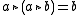Racks and quandles
Encyclopedia
In mathematics
, racks and quandles are sets with a binary operation
s satisfying axioms analogous to the Reidemeister move
s used to manipulate knot
diagrams.
While mainly used to obtain invariants of knots, they can be viewed as algebraic
constructions in their own right. In particular, the definition of a quandle axiomatizes the properties of conjugation
in a group
.
and Gavin Wraith, who at the time were undergraduate students at the University of Cambridge
. Wraith had become interested in these structures (which he initially dubbed sequentials) while at school. Conway renamed them wracks, partly as a pun on his colleague's name, and partly because they arise as the remnants (or 'wrack and ruin') of a group
when one discards the multiplicative structure and considers only the conjugation
structure. The spelling 'rack' has now become prevalent.
These constructs surfaced again in the 1980s: in a 1982 paper by David Joyce (where the term quandle was coined), in a 1982 paper by Sergei Matveev (under the name distributive groupoids) and in a 1986 conference paper by Egbert Brieskorn (where they were called automorphic sets). A detailed overview of racks and their applications in knot theory may be found in the paper by Colin Rourke and Roger Fenn.
set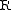
with a binary operation 
such that
for every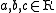
the self-distributive law holds: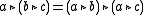
and for every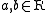
there exists a unique 
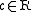such that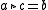
This definition, while terse and commonly used, is suboptimal for certain purposes because it contains an existential quantifier which is not really necessary. To avoid this,
we may write the unique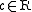
such that 
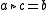as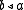 
. We then have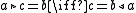
and thus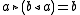
and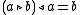
Using this idea, a rack may be equivalently defined as a set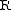
with two binary operations 
and
such that for all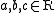 
:
It is convenient to say that the element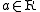
is acting from the left in the expression 
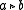, and acting from the right in the expression 
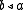. The third and fourth rack axioms then say that these left and right actions are inverses of each other. Using this, we can eliminate either one of these actions from the definition of rack. If we eliminate the right action and keep the left one, we obtain the terse definition given initially.
Many different conventions are used in the literature on racks and quandles. For example, many authors prefer to work with just the right action. Furthermore, the use of the symbols
and 
is by no means universal: many authors use exponential notation
and
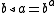
while many others write
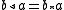
Yet another equivalent definition of a rack is that it is a set where each element acts on the left and right as automorphism
s of the rack, with the left action being the inverse of the right one. In this definition, the fact that each element acts as automorphisms encodes the left and right self-distributivity laws, and also these laws:
which are consequences of the definition(s) given earlier.
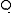such that 
or equivalently
In fact, every equational law satisfied by conjugation
in a group follows from the quandle axioms. So, one can think of a quandle as what is left of a group when we forget multiplication, the identity, and inverses, and only remember the operation of conjugation.
Every tame knot in three dimensional
Euclidean space
has a 'fundamental quandle'. To define this, one can note that the fundamental group
of the knot complement, or knot group
, has a presentation (the Wirtinger presentation) in which the relations only involve conjugation. So, this presentation can also be used as a presentation of a quandle. The fundamental quandle is a very powerful invariant of knots. In particular, if two knots have isomorphic fundamental quandles then there is a homeomorphism
of three-dimensional Euclidean space, which may be orientation reversing, taking one knot to the other.
Less powerful but more easily computable invariants of knots may be obtained by counting the homomorphisms from the knot quandle to a fixed quandle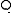
. Since the Wirtinger presentation has one generator for each strand in a knot diagram, these invariants can be computed by counting ways of labelling each strand by an element of 
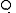, subject to certain constraints. More sophisticated invariants of this sort can be constructed with the help of quandle cohomology
.
The Alexander quandles are also important, since they can be used to compute the Alexander polynomial
of a knot. Let
be a module over the ring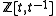 
of Laurent polynomials in one variable. Then the Alexander quandle is 
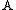made into a quandle with the left action given by
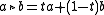
Racks are a useful generalization of quandles in topology, since while quandles can represent knots on a round linear object (such as rope or a thread), racks can represent ribbons, which may be twisted as well as knotted.
A quandle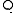
is said to be involutory if for all 
or equivalently
Any symmetric space
gives an involutory quandle, where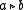
is the result of 'reflecting 
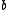through 
'.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, racks and quandles are sets with a binary operation
Binary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s satisfying axioms analogous to the Reidemeister move
Reidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
s used to manipulate knot
Knot theory
In topology, knot theory is the study of mathematical knots. While inspired by knots which appear in daily life in shoelaces and rope, a mathematician's knot differs in that the ends are joined together so that it cannot be undone. In precise mathematical language, a knot is an embedding of a...
diagrams.
While mainly used to obtain invariants of knots, they can be viewed as algebraic
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
constructions in their own right. In particular, the definition of a quandle axiomatizes the properties of conjugation
Conjugation
Conjugation or conjugate may refer to:* Conjugation , the modification of a verb from its basic form* Conjugate , used to rationalize the denominator of a fraction...
in a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
History
The earliest known work on racks is contained within (unpublished) 1959 correspondence between John ConwayJohn Horton Conway
John Horton Conway is a prolific mathematician active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory...
and Gavin Wraith, who at the time were undergraduate students at the University of Cambridge
University of Cambridge
The University of Cambridge is a public research university located in Cambridge, United Kingdom. It is the second-oldest university in both the United Kingdom and the English-speaking world , and the seventh-oldest globally...
. Wraith had become interested in these structures (which he initially dubbed sequentials) while at school. Conway renamed them wracks, partly as a pun on his colleague's name, and partly because they arise as the remnants (or 'wrack and ruin') of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
when one discards the multiplicative structure and considers only the conjugation
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
structure. The spelling 'rack' has now become prevalent.
These constructs surfaced again in the 1980s: in a 1982 paper by David Joyce (where the term quandle was coined), in a 1982 paper by Sergei Matveev (under the name distributive groupoids) and in a 1986 conference paper by Egbert Brieskorn (where they were called automorphic sets). A detailed overview of racks and their applications in knot theory may be found in the paper by Colin Rourke and Roger Fenn.
Racks
A rack may be defined as aset
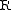with a binary operation such thatfor every
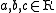the self-distributive law holds: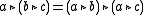 and for every
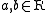there exists a unique 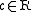such that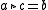This definition, while terse and commonly used, is suboptimal for certain purposes because it contains an existential quantifier which is not really necessary. To avoid this,
we may write the unique
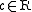such that 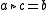as 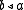. We then have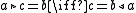and thus
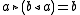
and
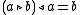
Using this idea, a rack may be equivalently defined as a set
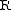with two binary operations and such that for all :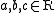
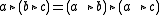(left self-distributive law) 
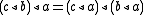(right self-distributive law)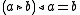 
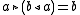
It is convenient to say that the element
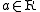is acting from the left in the expression 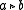, and acting from the right in the expression 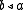. The third and fourth rack axioms then say that these left and right actions are inverses of each other. Using this, we can eliminate either one of these actions from the definition of rack. If we eliminate the right action and keep the left one, we obtain the terse definition given initially.Many different conventions are used in the literature on racks and quandles. For example, many authors prefer to work with just the right action. Furthermore, the use of the symbols
and is by no means universal: many authors use exponential notationand
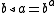
while many others write
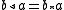
Yet another equivalent definition of a rack is that it is a set where each element acts on the left and right as automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s of the rack, with the left action being the inverse of the right one. In this definition, the fact that each element acts as automorphisms encodes the left and right self-distributivity laws, and also these laws:
which are consequences of the definition(s) given earlier.
Quandles
A quandle is defined as a rack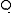 such that 
or equivalently
Examples and Applications
Every group gives a quandle where the operations come from conjugation:
In fact, every equational law satisfied by conjugation
Inner automorphism
In abstract algebra an inner automorphism is a functionwhich, informally, involves a certain operation being applied, then another one performed, and then the initial operation being reversed...
in a group follows from the quandle axioms. So, one can think of a quandle as what is left of a group when we forget multiplication, the identity, and inverses, and only remember the operation of conjugation.
Every tame knot in three dimensional
Three-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
has a 'fundamental quandle'. To define this, one can note that the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
of the knot complement, or knot group
Knot group
In mathematics, a knot is an embedding of a circle into 3-dimensional Euclidean space. The knot group of a knot K is defined as the fundamental group of the knot complement of K in R3,\pi_1....
, has a presentation (the Wirtinger presentation) in which the relations only involve conjugation. So, this presentation can also be used as a presentation of a quandle. The fundamental quandle is a very powerful invariant of knots. In particular, if two knots have isomorphic fundamental quandles then there is a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
of three-dimensional Euclidean space, which may be orientation reversing, taking one knot to the other.
Less powerful but more easily computable invariants of knots may be obtained by counting the homomorphisms from the knot quandle to a fixed quandle
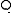. Since the Wirtinger presentation has one generator for each strand in a knot diagram, these invariants can be computed by counting ways of labelling each strand by an element of 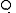, subject to certain constraints. More sophisticated invariants of this sort can be constructed with the help of quandle cohomologyCohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
.
The Alexander quandles are also important, since they can be used to compute the Alexander polynomial
Alexander polynomial
In mathematics, the Alexander polynomial is a knot invariant which assigns a polynomial with integer coefficients to each knot type. James Waddell Alexander II discovered this, the first knot polynomial, in 1923...
of a knot. Let
be a module over the ring 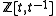of Laurent polynomials in one variable. Then the Alexander quandle is 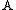made into a quandle with the left action given by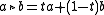Racks are a useful generalization of quandles in topology, since while quandles can represent knots on a round linear object (such as rope or a thread), racks can represent ribbons, which may be twisted as well as knotted.
A quandle
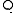is said to be involutory if for all 
or equivalently
Any symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
gives an involutory quandle, where
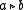is the result of 'reflecting 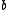through '.External links
- A Survey of Quandle Ideas by Scott Carter
- Knot Invariants Derived from Quandles and Racks by Seiichi Kamada
- Shelves, Racks, Spindles and Quandles in Lie 2-Algebras by Alissa Crans