
Rankin–Selberg method
Encyclopedia
In mathematics
, the Rankin–Selberg method, introduced by and , also known as the theory of integral representations of L-functions
, is a technique for directly constructing and analytically continuing
several important examples of automorphic L-functions
. Some authors reserve the term for a special type of integral representation, namely those that involve an Eisenstein series
. It has been one of the most powerful techniques for studying the Langlands program
.
, who constructed his zeta function as the Mellin transform
of Jacobi's theta function. Riemann used asymptotics of the theta function to obtain the analytic continuation, and the automorphy
of the theta function to prove the functional equation
. Erich Hecke
, and later Hans Maass
, applied the same Mellin transform method to modular form
s on the upper half-plane, after which Riemann's example can be seen as a special case.
Robert Alexander Rankin
and Atle Selberg
independently constructed their convolution
L-functions, now thought of as the Langlands L-function associated to the tensor product
of standard representation of GL
(2) with itself. Like Riemann, they used an integral of modular forms, but one of a different type: they integrated the product of two weight k modular forms f, g with a real analytic Eisenstein series
E(τ,s) over a fundamental domain D of the modular group SL2(Z) acting on the upper half plane.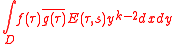
The integral converges absolutely if one of the two forms is cuspidal
; otherwise the asymptotics must be used to get a meromorphic
continuation like Riemann did. The analytic continuation and functional equation then boil down to those of the Eisenstein series. The integral was identified with the convolution L-function by a technique called "unfolding", in which the definition of the Eisenstein series and the range of integration are converted into a simpler expression that more readily exhibits the L-function as a Dirichlet series. The simultaneous combination of an unfolding together with global control over the analytic properties, is special and what makes the technique successful.
and Robert Langlands
later gave adelic
integral representations for the standard, and tensor product L-functions that had been earlier obtained by Riemann, Hecke, Maass, Rankin, and Selberg. They gave a very complete theory, in that they elucidated formulas for all local factors, stated the functional equation in a precise form, and gave sharp analytic continuations.
Thus, having an integral representation for an L-function by no means indicates its analytic properties are resolved: there may be serious analytic issues remaining. At minimum, though, it ensures the L-function has an algebraic construction through formal manipulations of an integral of automorphic forms, and that at all but a finite number of places it has the conjectured Euler product
of a particular L-function. In many situations the Langlands–Shahidi method
gives complementary information.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Rankin–Selberg method, introduced by and , also known as the theory of integral representations of L-functions
L-function
The theory of L-functions has become a very substantial, and still largely conjectural, part of contemporary analytic number theory. In it, broad generalisations of the Riemann zeta function and the L-series for a Dirichlet character are constructed, and their general properties, in most cases...
, is a technique for directly constructing and analytically continuing
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
several important examples of automorphic L-functions
Automorphic L-function
In mathematics, an automorphic L-function is a function L of a complex variable s, associated to an automorphic form π of a reductive group G over a global field and a finite-dimensional comlplex representation r of the Langlands dual group LG of G, generalizing the Dirichlet L-series of a...
. Some authors reserve the term for a special type of integral representation, namely those that involve an Eisenstein series
Eisenstein series
Eisenstein series, named after German mathematician Gotthold Eisenstein, are particular modular forms with infinite series expansions that may be written down directly...
. It has been one of the most powerful techniques for studying the Langlands program
Langlands program
The Langlands program is a web of far-reaching and influential conjectures that relate Galois groups in algebraic number theory to automorphic forms and representation theory of algebraic groups over local fields and adeles. It was proposed by ....
.
History
The theory in some sense dates back to Bernhard RiemannBernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, who constructed his zeta function as the Mellin transform
Mellin transform
In mathematics, the Mellin transform is an integral transform that may be regarded as the multiplicative version of the two-sided Laplace transform...
of Jacobi's theta function. Riemann used asymptotics of the theta function to obtain the analytic continuation, and the automorphy
Automorphic form
In mathematics, the general notion of automorphic form is the extension to analytic functions, perhaps of several complex variables, of the theory of modular forms...
of the theta function to prove the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
. Erich Hecke
Erich Hecke
Erich Hecke was a German mathematician. He obtained his doctorate in Göttingen under the supervision of David Hilbert. Kurt Reidemeister and Heinrich Behnke were among his students....
, and later Hans Maass
Hans Maass
Hans Maass was a German mathematician who introduced Maass wave forms and Koecher–Maass series and Maass–Selberg relations.-Publications:...
, applied the same Mellin transform method to modular form
Modular form
In mathematics, a modular form is a analytic function on the upper half-plane satisfying a certain kind of functional equation and growth condition. The theory of modular forms therefore belongs to complex analysis but the main importance of the theory has traditionally been in its connections...
s on the upper half-plane, after which Riemann's example can be seen as a special case.
Robert Alexander Rankin
Robert Alexander Rankin
Robert Alexander Rankin was a Scottish mathematician who worked in analytic number theory.Rankin's father, the Revd Oliver Shaw Rankin, was a minister who later became Professor of Old Testament Language, Literature and Theology in the University of Edinburgh.Rankin was born in Garlieston,...
and Atle Selberg
Atle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
independently constructed their convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
L-functions, now thought of as the Langlands L-function associated to the tensor product
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
of standard representation of GL
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
(2) with itself. Like Riemann, they used an integral of modular forms, but one of a different type: they integrated the product of two weight k modular forms f, g with a real analytic Eisenstein series
Real analytic Eisenstein series
In mathematics, the simplest real analytic Eisenstein series is a special function of two variables. It is used in the representation theory of SL and in analytic number theory...
E(τ,s) over a fundamental domain D of the modular group SL2(Z) acting on the upper half plane.
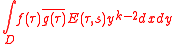
The integral converges absolutely if one of the two forms is cuspidal
Cusp form
In number theory, a branch of mathematics, a cusp form is a particular kind of modular form, distinguished in the case of modular forms for the modular group by the vanishing in the Fourier series expansion \Sigma a_n q^n...
; otherwise the asymptotics must be used to get a meromorphic
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
continuation like Riemann did. The analytic continuation and functional equation then boil down to those of the Eisenstein series. The integral was identified with the convolution L-function by a technique called "unfolding", in which the definition of the Eisenstein series and the range of integration are converted into a simpler expression that more readily exhibits the L-function as a Dirichlet series. The simultaneous combination of an unfolding together with global control over the analytic properties, is special and what makes the technique successful.
Modern adelic theory
Hervé JacquetHervé Jacquet
Hervé Jacquet is a French American mathematician born in France in 1939, working in automorphic forms. He is considered one of the founders of the theory of automorphic representations and their associated L-functions, and his results play a central role in modern number theory.-Career:Jacquet...
and Robert Langlands
Robert Langlands
Robert Phelan Langlands is a mathematician, best known as the founder of the Langlands program. He is an emeritus professor at the Institute for Advanced Study...
later gave adelic
Adele ring
In algebraic number theory and topological algebra, the adele ring is a topological ring which is built on the field of rational numbers . It involves all the completions of the field....
integral representations for the standard, and tensor product L-functions that had been earlier obtained by Riemann, Hecke, Maass, Rankin, and Selberg. They gave a very complete theory, in that they elucidated formulas for all local factors, stated the functional equation in a precise form, and gave sharp analytic continuations.
Generalizations and limitations
Nowadays one has integral representations for a large constellation of automorphic L-functions, however with two frustrating caveats. The first is that it is not at all clear which L-functions possibly have integral representations, or how they may be found; it is feared that the method is near exhaustion, though time and again new examples are found via clever arguments. The second is that in general it is difficult or perhaps even impossible to compute the local integrals after the unfolding stage. This means that the integrals may have the desired analytic properties, only that they may not represent an L-function (but instead something close to it).Thus, having an integral representation for an L-function by no means indicates its analytic properties are resolved: there may be serious analytic issues remaining. At minimum, though, it ensures the L-function has an algebraic construction through formal manipulations of an integral of automorphic forms, and that at all but a finite number of places it has the conjectured Euler product
Euler product
In number theory, an Euler product is an expansion of a Dirichlet series into an infinite product indexed by prime numbers. The name arose from the case of the Riemann zeta-function, where such a product representation was proved by Leonhard Euler.-Definition:...
of a particular L-function. In many situations the Langlands–Shahidi method
Langlands–Shahidi method
In mathematics, the Langlands–Shahidi method provides the means to define automorphic L-functions in many cases that arise with connected reductive groups over a number field. This includes Rankin–Selberg products for cuspidal automorphic representations of general linear groups...
gives complementary information.
Notable examples
- Standard L-functionStandard L-function- Standard L-function :In mathematics, the term Standard L-function refers to a particular type of automorphic L-function described by Robert P. Langlands....
on GL(n) (Godement–Jacquet). The theory was completely resolved in the original manuscript.
- Tensor product L-function on GL(n) × GL(m) (includes the standard L-function if m = 1), due to Jacquet, Ilya Piatetski-Shapiro, and Shalika. The theory was completely resolved by Moeglin–Waldspurger, and was reverse-engineered to establish the "converse theorem".
- Symmetric square on GL(n) due to Goro ShimuraGoro Shimurais a Japanese mathematician, and currently a professor emeritus of mathematics at Princeton University.Shimura was a colleague and a friend of Yutaka Taniyama...
, and Gelbart–Jacquet (n = 2), Piatetski-Shapiro and Patterson (n = 3), and Bump–Ginzburg (n > 3).
- Exterior square on GL(n), due to Jacquet–Shalika and Bump–Ginzburg.
- Triple Product on GL(2) × GL(2) × GL(2) (Garrett, as well as Harris, Ikeda, Piatetski-Shapiro, Rallis, Ramakrishnan, and Orloff).
- Symmetric cube on GL(2) (Bump–Ginzburg–Hoffstein).
- Symmetric fourth power on GL(2) (Ginzburg–Rallis).
- Standard L-function of E6 and E7 (Ginzburg).

