
Rational homotopy theory
Encyclopedia
In mathematics, rational homotopy theory is the study of the rational homotopy type of a space
, which means roughly that one ignores all torsion in the homotopy group
s. It was started by and .
Rational homotopy types of simply connected spaces can be identified with (isomorphism classes of) certain algebraic objects called minimal Sullivan algebras,
which are commutative
differential graded algebra
s over the rational number
s satisfying certain conditions.
The standard textbook on rational homotopy theory is .
all of whose homotopy groups are vector space
s over the rational numbers. If X is any simply connected CW complex
, then there is a rational space Y, unique up to homotopy equivalence, and a map from X to Y inducing an isomorphism
on homotopy groups tensored
with the rational numbers. The space Y is called the rationalization of X, and is the localization
of X at the rationals, and is the rational homotopy type of X. Informally, it is obtained from X by killing all torsion in the homotopy groups of X.
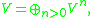
satisfying the following "nilpotence condition on d": V is the union of an increasing series of graded subspaces V(0)⊆V(1)⊆
where d = 0 on V(0) and d(V(k)) is contained in Λ(V(k − 1)). Here "commutative" means commutative in the graded sense, sometimes called supercommutative. Thus ab = (−1)deg(a)deg(b)ba.)
The Sullivan algebra is called minimal if the image of d is contained in Λ+(V)2, where Λ+(V) is the direct sum of the positive degree subspaces of Λ(V).
A Sullivan model for a commutative differential graded algebra A is an algebra homomorphism
from a Sullivan algebra Λ(V) that is an isomorphism on cohomology
. If A0 = Q then A has a minimal Sullivan model which is unique up to isomorphism. (Warning: a minimal Sullivan algebra with the same cohomology as A need not be a minimal Sullivan model for A: it is also necessary that the isomorphism of cohomology be induced by an algebra homomorphism. There are examples of non-isomorphic minimal Sullivan models with the same cohomology algebra.)
To any simply connected CW complex X with all rational homology groups of finite dimension one can assign a minimal Sullivan algebra ΛV of APL(X), which has the property that V1 = 0 and all the Vk of finite dimension. This is called the Sullivan minimal model of X, and is unique up to isomorphism. This gives an equivalence between rational homotopy types of such spaces and such algebras, such that:
When X is a smooth manifold, the differential algebra of smooth differential form
s on X (the de Rham complex
) is almost a model for X; more precisely it is the tensor product of a model for X with the reals and therefore determines the real homotopy type. One can go further and define the p-adic homotopy type and the adelic homotopy type and compare them to the rational homotopy type.
The results above for simply connected spaces can easily be extended to nilpotent spaces (whose fundamental group is nilpotent
and acts nilpotently on the higher homotopy groups). For more general fundamental groups things get more complicated; for example, the homotopy groups need not be finitely generated even if there are only a finite number of cells of the CW complex in each dimension.
Examples of formal spaces include spheres
, H-space
s, symmetric space
s, and compact
Kähler manifold
s . Formality is preserved under wedge sum
s and direct product
s; it is also preserved under connected sum
s for manifolds.
On the other hand, nilmanifold
s are almost never formal: if Mn is a compact formal nilmanifold, then Mn=Tn, the n-dimensional torus
. The simplest example of a non-formal compact nilmanifold is the Heisenberg manifold, the quotient of the Heisenberg group of 3×3 upper triangular matrices with 1's on the diagonal by its subgroup of matrices with integral coefficients. Symplectic manifold
s need not be formal: the simplest example is the Kodaira-Thurston manifold (the product of the Heisenberg manifold with a circle). Examples of non-formal, simply connected symplectic manifolds were given in .
Non-formality may often be detected by Massey product
s. Indeed, if a differential graded algebra A is formal, then all (higher order) Massey products must vanish. The converse is not true: formality means, roughly speaking, the "uniform" vanishing of all Massey products. The complement of the Borromean rings
is a non-formal space: it supports a non-trivial triple Massey product.
gave an algorithm for deciding whether or not a commutative differential graded algebra is formal.
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, which means roughly that one ignores all torsion in the homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s. It was started by and .
Rational homotopy types of simply connected spaces can be identified with (isomorphism classes of) certain algebraic objects called minimal Sullivan algebras,
which are commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
differential graded algebra
Differential graded algebra
In mathematics, in particular abstract algebra and topology, a differential graded algebra is a graded algebra with an added chain complex structure that respects the algebra structure.- Definition :...
s over the rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s satisfying certain conditions.
The standard textbook on rational homotopy theory is .
Rational spaces
A rational space is a simply connected spaceSimply connected space
In topology, a topological space is called simply connected if it is path-connected and every path between two points can be continuously transformed, staying within the space, into any other path while preserving the two endpoints in question .If a space is not simply connected, it is convenient...
all of whose homotopy groups are vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over the rational numbers. If X is any simply connected CW complex
CW complex
In topology, a CW complex is a type of topological space introduced by J. H. C. Whitehead to meet the needs of homotopy theory. This class of spaces is broader and has some better categorical properties than simplicial complexes, but still retains a combinatorial naturethat allows for...
, then there is a rational space Y, unique up to homotopy equivalence, and a map from X to Y inducing an isomorphism
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
on homotopy groups tensored
Tensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
with the rational numbers. The space Y is called the rationalization of X, and is the localization
Localization of a topological space
In mathematics, well behaved topological spaces can be localized at primes, in a similar way to the localization of a ring at a prime. This construction was described by Dennis Sullivan in 1970 lecture notes that were finally published in ....
of X at the rationals, and is the rational homotopy type of X. Informally, it is obtained from X by killing all torsion in the homotopy groups of X.
Sullivan algebras
A Sullivan algebra is a commutative differential graded algebra over the rationals Q, whose underlying algebra is the free commutative graded algebra Λ(V) on a graded vector space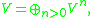
satisfying the following "nilpotence condition on d": V is the union of an increasing series of graded subspaces V(0)⊆V(1)⊆
where d = 0 on V(0) and d(V(k)) is contained in Λ(V(k − 1)). Here "commutative" means commutative in the graded sense, sometimes called supercommutative. Thus ab = (−1)deg(a)deg(b)ba.)
The Sullivan algebra is called minimal if the image of d is contained in Λ+(V)2, where Λ+(V) is the direct sum of the positive degree subspaces of Λ(V).
A Sullivan model for a commutative differential graded algebra A is an algebra homomorphism
Algebra homomorphism
A homomorphism between two algebras, A and B, over a field K, is a map F:A\rightarrow B such that for all k in K and x,y in A,* F = kF* F = F + F...
from a Sullivan algebra Λ(V) that is an isomorphism on cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
. If A0 = Q then A has a minimal Sullivan model which is unique up to isomorphism. (Warning: a minimal Sullivan algebra with the same cohomology as A need not be a minimal Sullivan model for A: it is also necessary that the isomorphism of cohomology be induced by an algebra homomorphism. There are examples of non-isomorphic minimal Sullivan models with the same cohomology algebra.)
The Sullivan minimal model of a topological space
For any topological space X Sullivan defined a commutative differential graded algebra APL(X), called the algebra of polynomial differential forms on X with rational coefficients. An element of this algebra consists of (roughly) a polynomial form on each singular simplex of X, compatible with face and degeneracy maps. This algebra is usually very large (uncountable dimension) but can be replaced by a much smaller algebra. More precisely, any differential graded algebra with the same Sullivan minimal model as APL(X) is called a model for the space X, and determines the rational homotopy type of X when X is simply connected.To any simply connected CW complex X with all rational homology groups of finite dimension one can assign a minimal Sullivan algebra ΛV of APL(X), which has the property that V1 = 0 and all the Vk of finite dimension. This is called the Sullivan minimal model of X, and is unique up to isomorphism. This gives an equivalence between rational homotopy types of such spaces and such algebras, such that:
- The rational cohomology of the space is the cohomology of its Sullivan minimal model.
- The spaces of indecomposables in V are the duals of the rational homotopy groups of the space X.
- The Whitehead product on rational homotopy is the dual of the "quadratic part" of the differential d.
- Two spaces have the same rational homotopy type if and only if their minimal Sullivan algebras are isomorphic.
- There is a simply connected space X corresponding to each possible Sullivan algebra with V1 = 0 and all the Vk of finite dimension.
When X is a smooth manifold, the differential algebra of smooth differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on X (the de Rham complex
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
) is almost a model for X; more precisely it is the tensor product of a model for X with the reals and therefore determines the real homotopy type. One can go further and define the p-adic homotopy type and the adelic homotopy type and compare them to the rational homotopy type.
The results above for simply connected spaces can easily be extended to nilpotent spaces (whose fundamental group is nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
and acts nilpotently on the higher homotopy groups). For more general fundamental groups things get more complicated; for example, the homotopy groups need not be finitely generated even if there are only a finite number of cells of the CW complex in each dimension.
Formal spaces
A commutative differential graded algebra A, again with A0 = Q, is called formal if A has a model with vanishing differential. This is equivalent to requiring that the cohomology algebra of A (viewed as a differential algebra with trivial differential) is a model for A. Thus two formal commutative differential graded algebras with the isomorphic cohomology algebras have the same Sullivan minimal model. A space is called formal if its minimal Sullivan model is formal, so the minimal Sullivan model of a simply connected formal topological space is determined by the rational cohomology ring. This means that the rational homotopy of a formal space is particularly easy to work out.Examples of formal spaces include spheres
Hypersphere
In mathematics, an n-sphere is a generalization of the surface of an ordinary sphere to arbitrary dimension. For any natural number n, an n-sphere of radius r is defined as the set of points in -dimensional Euclidean space which are at distance r from a central point, where the radius r may be any...
, H-space
H-space
In mathematics, an H-space is a topological space X together with a continuous map μ : X × X → X with an identity element e so that μ = μ = x for all x in X...
s, symmetric space
Symmetric space
A symmetric space is, in differential geometry and representation theory, a smooth manifold whose group of symmetries contains an "inversion symmetry" about every point...
s, and compact
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Kähler manifold
Kähler manifold
In mathematics, a Kähler manifold is a manifold with unitary structure satisfying an integrability condition.In particular, it is a Riemannian manifold, a complex manifold, and a symplectic manifold, with these three structures all mutually compatible.This threefold structure corresponds to the...
s . Formality is preserved under wedge sum
Wedge sum
In topology, the wedge sum is a "one-point union" of a family of topological spaces. Specifically, if X and Y are pointed spaces the wedge sum of X and Y is the quotient of the disjoint union of X and Y by the identification x0 ∼ y0:X\vee Y = \;/ \sim,\,where ∼ is the...
s and direct product
Direct product
In mathematics, one can often define a direct product of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets, together with a suitably defined structure on the product set....
s; it is also preserved under connected sum
Connected sum
In mathematics, specifically in topology, the operation of connected sum is a geometric modification on manifolds. Its effect is to join two given manifolds together near a chosen point on each...
s for manifolds.
On the other hand, nilmanifold
Nilmanifold
In mathematics, a nilmanifold is a differentiable manifold which has a transitive nilpotent group of diffeomorphisms acting on it. As such, a nilmanifold is an example of a homogeneous space and is diffeomorphic to the quotient space N/H, the quotient of a nilpotent Lie group N modulo a closed...
s are almost never formal: if Mn is a compact formal nilmanifold, then Mn=Tn, the n-dimensional torus
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
. The simplest example of a non-formal compact nilmanifold is the Heisenberg manifold, the quotient of the Heisenberg group of 3×3 upper triangular matrices with 1's on the diagonal by its subgroup of matrices with integral coefficients. Symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
s need not be formal: the simplest example is the Kodaira-Thurston manifold (the product of the Heisenberg manifold with a circle). Examples of non-formal, simply connected symplectic manifolds were given in .
Non-formality may often be detected by Massey product
Massey product
In algebraic topology, the Massey product is a cohomology operation of higher order introduced in , which generalizes the cup product.-Massey triple product:...
s. Indeed, if a differential graded algebra A is formal, then all (higher order) Massey products must vanish. The converse is not true: formality means, roughly speaking, the "uniform" vanishing of all Massey products. The complement of the Borromean rings
Borromean rings
In mathematics, the Borromean rings consist of three topological circles which are linked and form a Brunnian link, i.e., removing any ring results in two unlinked rings.- Mathematical properties :...
is a non-formal space: it supports a non-trivial triple Massey product.
gave an algorithm for deciding whether or not a commutative differential graded algebra is formal.
Examples
- If X is a sphere of odd dimension 2n + 1 > 1, its minimal Sullivan model has 1 generator a of degree 2n + 1 with da = 0, and a basis of elements 1, a.
- If X is a sphere of even dimension 2n > 0, its minimal Sullivan model has 2 generators a and b of degrees 2n and 4n − 1, with db = a2, da = 0, and a basis of elements 1, a, b→ a2, ab→a3, a2b→a4, ... where the arrow indicated the action of d.
- Suppose that V has 4 elements a, b, x, y of degrees 2, 3, 3 and 4 with differentials da = 0, db = 0, dx = a2, dy = ab. Then this algebra is a minimal Sullivan algebra that is not formal. The cohomology algebra has nontrivial components only in dimension 2,3,6, generated respectively by a, b and cb-ad. Any homomorphism from V to its cohomology algebra would map d to 0, c to a multiple of b, so it would surely map cb-ad to 0. So V cannot be a model for its cohomology algebra. The corresponding topological spaces are two spaces with the same rational cohomology ringCohomology ringIn mathematics, specifically algebraic topology, the cohomology ring of a topological space X is a ring formed from the cohomology groups of X together with the cup product serving as the ring multiplication. Here 'cohomology' is usually understood as singular cohomology, but the ring structure is...
but different rational homotopy types.
External links
- Rational Homotopy Theory: A Brief Introduction by Kathryn Hess

