
Read only right moving Turing Machines
Encyclopedia
Read-only right moving Turing Machines are a particular type of Turing Machine
.
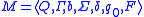 where
where
In the case of these types of Turing Machines, the only movement is to the right.
There must exist at least one element of the set (a HALT state) for the machine to accept a regular language (Not in including the empty language).
(a HALT state) for the machine to accept a regular language (Not in including the empty language).
An example Read Only right moving Turing machine
State table for 3 state, 2 symbol read only machine:
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
.
Definition
The definition based on a single infinite tape defined to be a 7-tupleTuple
In mathematics and computer science, a tuple is an ordered list of elements. In set theory, an n-tuple is a sequence of n elements, where n is a positive integer. There is also one 0-tuple, an empty sequence. An n-tuple is defined inductively using the construction of an ordered pair...
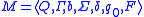 where
where
-
 is a finite set of states
is a finite set of states -
 is a finite set of the tape alphabet/symbols
is a finite set of the tape alphabet/symbols -
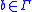 is the blank symbol (the only symbol allowed to occur on the tape infinitely often at any step during the computation)
is the blank symbol (the only symbol allowed to occur on the tape infinitely often at any step during the computation) -
 , a subset of
, a subset of  not including b is the set of input symbols
not including b is the set of input symbols -
 is a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is a functionFunction (mathematics)In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
called the transition functionTransition functionIn mathematics, a transition function has several different meanings:* In topology, a transition function is a homeomorphism from one coordinate chart to another...
, R is a right movement (a right shift). -
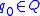 is the initial state
is the initial state -
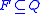 is the set of final or accepting states
is the set of final or accepting states
In the case of these types of Turing Machines, the only movement is to the right.
There must exist at least one element of the set
 (a HALT state) for the machine to accept a regular language (Not in including the empty language).
(a HALT state) for the machine to accept a regular language (Not in including the empty language).An example Read Only right moving Turing machine
- Q = { A, B, C, HALT }
- Γ = { 0, 1 }
- b = 0 = "blank"
- Σ =
 , empty set
, empty set - δ = see state-table below
- q0 = A = initial state
- F = the one element set of final states {HALT}
State table for 3 state, 2 symbol read only machine:
| Current state A: | Current state B: | Current state C: | |||||||
| Write symbol: | Move tape: | Next state: | Write symbol: | Move tape: | Next state: | Write symbol: | Move tape: | Next state: | |
| tape symbol is 0: | 1 | R |
B | 1 | R |
A | 1 | R |
B | ||||||
| tape symbol is 1: | 1 | R |
C | 1 | R |
B | 1 | N | HALT |
See also
- DFADeterministic finite state machineIn the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
- NDFANondeterministic finite state machineIn the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
- Finite State MachineFinite state machineA finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
- Read-only Turing machineRead-only Turing machineA read-only Turing machine or Two-way deterministic finite-state automaton is class of models of computability that behave like a standard Turing machine and can move in both directions across input, except cannot write to its input tape...
- Turing MachineTuring machineA Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
- Turing machine examplesTuring machine examples-Turing's very first example:The following table is Turing's very first example :With regard to what actions the machine actually does, Turing states the following:...

