Read-only Turing machine
Encyclopedia
A read-only Turing machine or Two-way deterministic finite-state automaton (2DFA) is class of models of computability that behave like a standard Turing machine
and can move in both directions across input, except cannot write to its input tape. The machine in its bare form is equivalent to a Deterministic finite-state machine or DFA in computational power, and therefore can only parse a regular language
.
where
So given initial state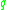
reading symbol 
, we have a transition defined by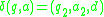 
which replaces 
with 
, transitions to state 
, and moves the "read head" in direction 
(left or right) to read the next input. In our 2DFA read-only machine, however,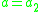 
always.
This model is now equivalent to a DFA. The proof is outlined by noting that a Nondeterministic finite state machine
(NFA) can model a 2DFA by offering both leftward and rightward movement of the read head as possible transitions. The NFA is then reducible to a DFA by a well-established proof (see article for details). The 2DFA can model a standard DFA quite easily by simply having all transitions move the head in one direction.
Other variants of this model allow more computational complexity
. With a single infinite stack
the model can parse (at least) any language that is computable by a Turing machine in linear time. In particular, the language {anbncn} can be parsed by an algorithm which verifies first that there are the same number of a's and b's, then rewinds and verifies that there are the same number of b's and c's. With the further aid of nondeterminism
the machine can parse any context-free language
. With two infinite stacks the machine is Turing equivalent and can parse any recursive formal language
.
If the machine is allowed to have multiple tape heads, it can parse any language in L
or NL
, according to whether nondeterminism is allowed.
to accept the definition of the Turing machine that is to be modelled, after which computation continues with a standard Turing machine.
In modern research, the model has become important in describing a new complexity class of Quantum finite automata
or deterministic probabilistic automata
.
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
and can move in both directions across input, except cannot write to its input tape. The machine in its bare form is equivalent to a Deterministic finite-state machine or DFA in computational power, and therefore can only parse a regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
.
Theory
We define a standard Turing machine by the 9-tuple where-
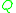is a finite set of states; -
is the finite set of the input alphabet; -
is the finite tape alphabet; -
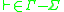is the left endmarker; -
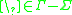is the blank symbol; -
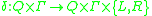is the transition function; -
is the start state; -
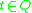is the accept state; -
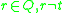is the reject state.
So given initial state
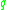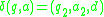reading symbol , we have a transition defined by which replaces with , transitions to state , and moves the "read head" in direction (left or right) to read the next input. In our 2DFA read-only machine, however, 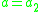always.This model is now equivalent to a DFA. The proof is outlined by noting that a Nondeterministic finite state machine
Nondeterministic finite state machine
In the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
(NFA) can model a 2DFA by offering both leftward and rightward movement of the read head as possible transitions. The NFA is then reducible to a DFA by a well-established proof (see article for details). The 2DFA can model a standard DFA quite easily by simply having all transitions move the head in one direction.
Variants
Several variants of this model are also equivalent to DFAs. In particular, the nondeterministic case (in which the transition from one state can be to multiple states given the same input) is reducible to a DFA.Other variants of this model allow more computational complexity
Computational Complexity
Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...
. With a single infinite stack
Stack (data structure)
In computer science, a stack is a last in, first out abstract data type and linear data structure. A stack can have any abstract data type as an element, but is characterized by only three fundamental operations: push, pop and stack top. The push operation adds a new item to the top of the stack,...
the model can parse (at least) any language that is computable by a Turing machine in linear time. In particular, the language {anbncn} can be parsed by an algorithm which verifies first that there are the same number of a's and b's, then rewinds and verifies that there are the same number of b's and c's. With the further aid of nondeterminism
Nondeterministic finite state machine
In the automata theory, a nondeterministic finite state machine or nondeterministic finite automaton is a finite state machine where from each state and a given input symbol the automaton may jump into several possible next states...
the machine can parse any context-free language
Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.-Examples:...
. With two infinite stacks the machine is Turing equivalent and can parse any recursive formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
.
If the machine is allowed to have multiple tape heads, it can parse any language in L
L (complexity)
In computational complexity theory, L is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a logarithmic amount of memory space...
or NL
NL (complexity)
In computational complexity theory, NL is the complexity class containing decision problems which can be solved by a nondeterministic Turing machine using a logarithmic amount of memory space....
, according to whether nondeterminism is allowed.
Applications
A read-only Turing machine is used in the definition of a Universal Turing machineUniversal Turing machine
In computer science, a universal Turing machine is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input thereof from its own tape. Alan...
to accept the definition of the Turing machine that is to be modelled, after which computation continues with a standard Turing machine.
In modern research, the model has become important in describing a new complexity class of Quantum finite automata
Quantum finite automata
In quantum computing, quantum finite automata or QFA are a quantum analog of probabilistic automata. They are related to quantum computers in a similar fashion as finite automata are related to Turing machines. Several types of automata may be defined, including measure-once and measure-many automata...
or deterministic probabilistic automata
Probabilistic automaton
In mathematics and computer science, the probabilistic automaton is a generalization of the non-deterministic finite automaton; it includes the probability of a given transition into the transition function, turning it into a transition matrix or stochastic matrix. Thus, the probabilistic...
.
See also
- Computability
- Turing machine equivalentsTuring machine equivalentsThe following article is a referral from the article Turing machine. Many of the machines described here have articles that offer much more information.- Machines equivalent to the Turing machine model :Turing equivalence:...
- Stack machineStack machineA stack machine may be* A real or emulated computer that evaluates each sub-expression of a program statement via a pushdown data stack and uses a reverse Polish notation instruction set....
- Queue machineQueue machineA queue machine or queue automaton is a finite state machine with the ability to store and retrieve data from an infinite-memory queue. It is a model of computation equivalent to a Turing machine, and therefore it can process any formal language....
- Quantum computerQuantum computerA quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...