Quantum finite automata
Encyclopedia
In quantum computing, quantum finite automata or QFA are a quantum analog of probabilistic automata. They are related to quantum computer
s in a similar fashion as finite automata are related to Turing machine
s. Several types of automata may be defined, including measure-once and measure-many automata. Quantum finite automata can also be understood as the quantization of subshifts of finite type, or as a quantization of Markov chain
s. QFA's are, in turn, special cases of geometric finite automata or topological finite automata.
The automata work by accepting a finite-length string
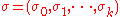of letters 
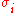from a finite alphabet 
, and assigning to each such string a probability
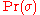indicating the probability of the automaton being in an accept state; that is, indicating whether the automaton accepted or rejected the string.
As with an ordinary finite automaton, the quantum automaton is considered to have
possible internal states, represented in this case by an 
-state qubit
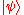. More precisely, the 
-state qubit 
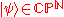is an element of 
-dimensional complex projective space
, carrying an inner product
that is the Fubini-Study metric
.
The state transitions, transition matrixes or de Bruijn graph
s are represented by a collection of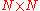
unitary matrixes 
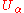, with one unitary matrix for each letter 
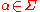. That is, given an input letter 
, the unitary matrix describes the transition of the automaton from its current state 
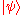to its next state 
:
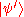Thus, the triple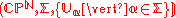
form a quantum semiautomaton.
The accept state of the automaton is given by an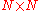
projection matrix 
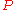, so that, given a 
-dimensional quantum state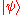 
, the probability of 
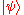being in the accept state is
The probability of the state machine accepting a given finite input string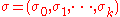
is given by
Here, the vector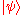
is understood to represent the initial state of the automaton, that is, the state the automaton was in before it stated accepting the string input. The empty string 
is understood to be just the unit matrix, so that
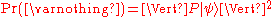
is just the probability of the initial state being an accepted state.
Because the left-action of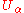
on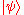 
reverses the order of the letters in the string 
, it is not uncommon for QFA's to be defined using a right action on the Hermitian transpose states, simply in order to keep the order of the letters the same.
A regular language
is accepted with probability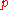
by a quantum finite automaton, if, for all sentences 
in the language, (and a given, fixed initial state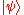 
), one has 
.
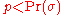given by the state transition table
The quantum state is a vector, in bra-ket notation
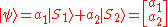
with the complex number
s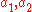
normalized so that
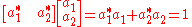
The unitary transition matrices are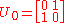
and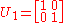
Taking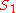
to be the accept state, the projection matrix is
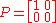
As should be readily apparent, if the initial state is the pure state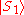
or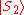 
, then the result of running the machine will be exactly identical to the classical deterministic finite state machine. In particular, there is a language accepted by this automaton with probability one, for these initial states, and it is identical to the regular language
for the classical DFA, and is given by the regular expression
:
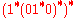
The non-classical behaviour occurs if both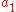
and 
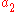are non-zero. More subtle behaviour occurs when the matrices 
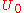and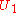 
are not so simple; see, for example, the de Rham curve
as an example of a quantum finite state machine acting on the set of all possible finite binary strings.
The Hilbert space
is decomposed into three orthogonal subspaces
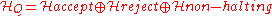
In the literature, these orthogonal subspaces are usually formulated in terms of the set
of orthogonal basis vectors for the Hilbert space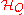 
. This set of basis vectors is divided up into subsets 
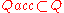and 
, such that
is the linear span
of the basis vectors in the accept set. The reject space is defined analogously, and the remaining space is designated the non-halting subspace. There are three projection matrices,
, 
and 
, each projecting to the respective subspace:
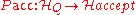
and so on. The parsing of the input string proceeds as follows. Consider the automaton to be in a state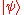
. After reading an input letter 
, the automaton will be in the state
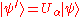
At this point, a measurement is performed on the state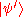
, using the projection operators 
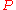, at which time its wave-function collapses into one of the three subspaces 
or 
or 
. The probability of collapse is given by
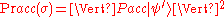
for the "accept" subspace, and analogously for the other two spaces.
If the wave function has collapsed to either the "accept" or "reject" subspaces, then further processing halts. Otherwise, processing continues, with the next letter read from the input, and applied to what must be an eigenstate of
. Processing continues until the whole string is read, or the machine halts. Often, additional symbols 
and $ are adjoined to the alphabet, to act as the left and right end-markers for the string.
In the literature, the meaure-many automaton is often denoted by the tuple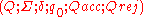
. Here, 
, 
, 
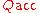and 
are as defined above. The initial state is denoted by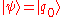 
. The unitary transformations are denoted by the map 
,
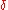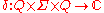
so that
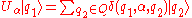
s. For example, one may take some (N-dimensional) Riemann symmetric space to take the place of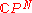
. In place of the unitary matrices, one uses the isometries
of the Riemannian manifold, or, more generally, some set of open functions appropriate for the given topological space. The initial state may be taken to be a point in the space. The set of accept states can be taken to be some arbitrary subset of the topological space. One then says that a formal language
is accepted by this topological automaton if the point, after iteration by the homeomorphisms, intersects the accept set. But, of course, this is nothing more than the standard definition of an M-automaton. The behaviour of topological automata is studied in the field of topological dynamics
.
The quantum automaton differs from the topological automaton in that, instead of having a binary result (is the iterated point in, or not in, the final set?), one has a probability. The quantum probability is the (square of) the initial state projected onto some final state P; that is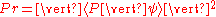
. But this probability amplitude is just a very simple function of the distance between the point 
and the point 
in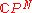 
, under the distance metric
given by the Fubini-Study metric
. To recap, the quantum probability of a language being accepted can be interpreted as a metric, with the probability of accept being unity, if the metric distance between the initial and final states is zero, and otherwise the probability of accept is less than one, if the metric distance is non-zero. Thus, it follows that the quantum finite automaton is just a special case of a geometric automaton or a metric automaton, where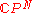
is generalized to some metric space
, and the probability measure is replaced by a simple function of the metric on that space.
Quantum computer
A quantum computer is a device for computation that makes direct use of quantum mechanical phenomena, such as superposition and entanglement, to perform operations on data. Quantum computers are different from traditional computers based on transistors...
s in a similar fashion as finite automata are related to Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
s. Several types of automata may be defined, including measure-once and measure-many automata. Quantum finite automata can also be understood as the quantization of subshifts of finite type, or as a quantization of Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
s. QFA's are, in turn, special cases of geometric finite automata or topological finite automata.
The automata work by accepting a finite-length string
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
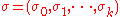of letters 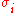from a finite alphabet , and assigning to each such string a probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
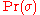indicating the probability of the automaton being in an accept state; that is, indicating whether the automaton accepted or rejected the string.Measure-once automata
Measure-once automata were introduced by Moore and Crutchfield. They may be defined formally as follows.As with an ordinary finite automaton, the quantum automaton is considered to have
possible internal states, represented in this case by an -state qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
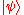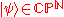. More precisely, the -state qubit is an element of -dimensional complex projective spaceComplex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, carrying an inner product
that is the Fubini-Study metricFubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
.
The state transitions, transition matrixes or de Bruijn graph
De Bruijn graph
In graph theory, an n-dimensional De Bruijn graph of m symbols is a directed graph representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence...
s are represented by a collection of
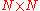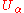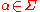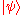unitary matrixes , with one unitary matrix for each letter . That is, given an input letter , the unitary matrix describes the transition of the automaton from its current state to its next state 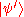:Thus, the triple
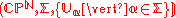form a quantum semiautomaton.The accept state of the automaton is given by an
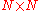projection matrix 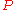, so that, given a -dimensional quantum state 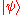, the probability of 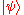being in the accept state isThe probability of the state machine accepting a given finite input string
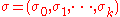is given byHere, the vector
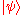is understood to represent the initial state of the automaton, that is, the state the automaton was in before it stated accepting the string input. The empty string is understood to be just the unit matrix, so that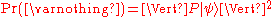is just the probability of the initial state being an accepted state.
Because the left-action of
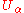on 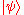reverses the order of the letters in the string , it is not uncommon for QFA's to be defined using a right action on the Hermitian transpose states, simply in order to keep the order of the letters the same.A regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
is accepted with probability
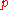by a quantum finite automaton, if, for all sentences in the language, (and a given, fixed initial state 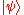), one has 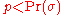.Example
Consider the classical deterministic finite state machineDeterministic finite state machine
In the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
given by the state transition table
State transition table
In automata theory and sequential logic, a state transition table is a table showing what state a finite semiautomaton or finite state machine will move to, based on the current state and other inputs...
EWLINE
|
State Diagram  |
The quantum state is a vector, in bra-ket notation
Bra-ket notation
Bra-ket notation is a standard notation for describing quantum states in the theory of quantum mechanics composed of angle brackets and vertical bars. It can also be used to denote abstract vectors and linear functionals in mathematics...
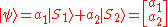
with the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s
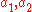normalized so that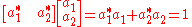The unitary transition matrices are
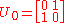
and
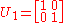
Taking
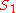to be the accept state, the projection matrix is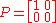As should be readily apparent, if the initial state is the pure state
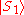or 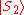, then the result of running the machine will be exactly identical to the classical deterministic finite state machine. In particular, there is a language accepted by this automaton with probability one, for these initial states, and it is identical to the regular languageRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
for the classical DFA, and is given by the regular expression
Regular expression
In computing, a regular expression provides a concise and flexible means for "matching" strings of text, such as particular characters, words, or patterns of characters. Abbreviations for "regular expression" include "regex" and "regexp"...
:
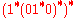
The non-classical behaviour occurs if both
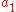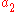and are non-zero. More subtle behaviour occurs when the matrices 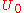and 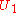are not so simple; see, for example, the de Rham curveDe Rham curve
In mathematics, a de Rham curve is a certain type of fractal curve named in honor of Georges de Rham.The Cantor function, Césaro curve, Minkowski's question mark function, the Lévy C curve, the blancmange curve and the Koch curve are all special cases of the general de Rham...
as an example of a quantum finite state machine acting on the set of all possible finite binary strings.
Measure-many automata
Measure-many automata were introduced by Kondacs and Watrous in 1997.. The general framework resembles that of the measure-once automaton, except that instead of there being one projection, at the end, there is a projection, or quantum measurement, performed after each letter is read. A formal definition follows.The Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
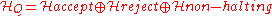
is decomposed into three orthogonal subspacesIn the literature, these orthogonal subspaces are usually formulated in terms of the set
of orthogonal basis vectors for the Hilbert space 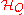. This set of basis vectors is divided up into subsets 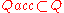and , such thatis the linear span
Linear span
In the mathematical subfield of linear algebra, the linear span of a set of vectors in a vector space is the intersection of all subspaces containing that set...
of the basis vectors in the accept set. The reject space is defined analogously, and the remaining space is designated the non-halting subspace. There are three projection matrices,
, and , each projecting to the respective subspace: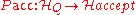and so on. The parsing of the input string proceeds as follows. Consider the automaton to be in a state
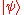. After reading an input letter , the automaton will be in the state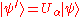At this point, a measurement is performed on the state
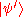, using the projection operators 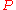, at which time its wave-function collapses into one of the three subspaces or or . The probability of collapse is given by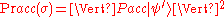for the "accept" subspace, and analogously for the other two spaces.
If the wave function has collapsed to either the "accept" or "reject" subspaces, then further processing halts. Otherwise, processing continues, with the next letter read from the input, and applied to what must be an eigenstate of
. Processing continues until the whole string is read, or the machine halts. Often, additional symbols and $ are adjoined to the alphabet, to act as the left and right end-markers for the string.In the literature, the meaure-many automaton is often denoted by the tuple
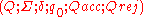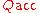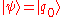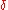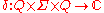
. Here, , , and are as defined above. The initial state is denoted by . The unitary transformations are denoted by the map ,so that
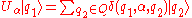
Geometric generalizations
The above constructions indicate how the concept of a quantum finite automaton can be generalized to arbitrary topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s. For example, one may take some (N-dimensional) Riemann symmetric space to take the place of
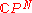. In place of the unitary matrices, one uses the isometriesIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of the Riemannian manifold, or, more generally, some set of open functions appropriate for the given topological space. The initial state may be taken to be a point in the space. The set of accept states can be taken to be some arbitrary subset of the topological space. One then says that a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
is accepted by this topological automaton if the point, after iteration by the homeomorphisms, intersects the accept set. But, of course, this is nothing more than the standard definition of an M-automaton. The behaviour of topological automata is studied in the field of topological dynamics
Topological dynamics
In mathematics, topological dynamics is a branch of the theory of dynamical systems in which qualitative, asymptotic properties of dynamical systems are studied from the viewpoint of general topology.- Scope :...
.
The quantum automaton differs from the topological automaton in that, instead of having a binary result (is the iterated point in, or not in, the final set?), one has a probability. The quantum probability is the (square of) the initial state projected onto some final state P; that is
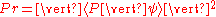. But this probability amplitude is just a very simple function of the distance between the point and the point in 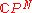, under the distance metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
given by the Fubini-Study metric
Fubini-Study metric
In mathematics, the Fubini–Study metric is a Kähler metric on projective Hilbert space, that is, complex projective space CPn endowed with a Hermitian form. This metric was originally described in 1904 and 1905 by Guido Fubini and Eduard Study....
. To recap, the quantum probability of a language being accepted can be interpreted as a metric, with the probability of accept being unity, if the metric distance between the initial and final states is zero, and otherwise the probability of accept is less than one, if the metric distance is non-zero. Thus, it follows that the quantum finite automaton is just a special case of a geometric automaton or a metric automaton, where
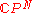is generalized to some metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, and the probability measure is replaced by a simple function of the metric on that space.