
Probabilistic automaton
Encyclopedia
In mathematics
and computer science
, the probabilistic automaton (PA) is a generalization of the non-deterministic finite automaton; it includes the probability of a given transition into the transition function
, turning it into a transition matrix or stochastic matrix
. Thus, the probabilistic automaton generalizes the concept of a Markov chain
or subshift of finite type
. The languages
recognized by probabilistic automata are called stochastic languages; these include the regular language
s as a subset. The number of stochastic languages is uncountable.
The concept was introduced by Michael O. Rabin
in 1963; a certain special case is sometimes known as the Rabin automaton. In recent years, a variant has been formulated in terms of quantum probabilities, the quantum finite automaton.
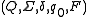 , together with two probabilities: the probability
, together with two probabilities: the probability  of a particular state transition taking place, and with the initial state
of a particular state transition taking place, and with the initial state  replaced by a stochastic vector giving the probability of the automaton being in a given initial state.
replaced by a stochastic vector giving the probability of the automaton being in a given initial state.
For the ordinary non-deterministic finite automaton, one has
Here, denotes the power set of
denotes the power set of  .
.
By use of currying
, the transition function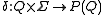 of a non-deterministic finite automaton can be written as a membership function
of a non-deterministic finite automaton can be written as a membership function
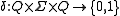
so that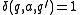 if
if 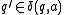 and
and  if
if 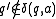 . The curried transition function can be understood to be a matrix with matrix entries
. The curried transition function can be understood to be a matrix with matrix entries
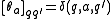
The matrix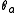 is then a square matrix, whose entries are zero or one, indicating whether a transition
is then a square matrix, whose entries are zero or one, indicating whether a transition 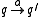 is allowed by the NFA. Such a transition matrix is always defined for a non-deterministic finite automaton.
is allowed by the NFA. Such a transition matrix is always defined for a non-deterministic finite automaton.
The probabilistic automaton replaces this matrix by a stochastic matrix
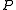 , so that the probability of a transition is given by
, so that the probability of a transition is given by
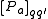
A state change from some state to any state must occur with probability one, of course, and so one must have
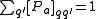
for all input letters and internal states
and internal states 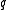 . The initial state of a probabilistic automaton is given by a row vector
. The initial state of a probabilistic automaton is given by a row vector  , whose components add to unity:
, whose components add to unity:
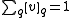
The transition matrix acts on the right, so that the state of the probabilistic automaton, after consuming the input string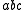 , would be
, would be
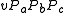
In particular, the state of a probabilistic automaton is always a stochastic vector, since the product of any two stochastic matrices is a stochastic matrix, and the product of a stochastic vector and a stochastic matrix is again a stochastic vector. This vector is sometimes called the distribution of states, emphasizing that it is a discrete probability distribution.
Formally, the definition of a probabilistic automaton does not require the mechanics of the non-deterministic automaton, which may be dispensed with. Formally, a probabilistic automaton PA is defined as the tuple . A Rabin automaton is one for which the initial distribution
. A Rabin automaton is one for which the initial distribution  is a coordinate vector
is a coordinate vector
; that is, has zero for all but one entries, and the remaining entry being one.
recognized by probabilistic automata are called stochastic languages. They include the regular language
s as a subset.
Let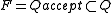 be the set of "accepting" or "final" states of the automaton. By abuse of notation,
be the set of "accepting" or "final" states of the automaton. By abuse of notation, 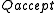 can also be understood to be the column vector that is the membership function for
can also be understood to be the column vector that is the membership function for 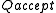 ; that is, it has a 1 at the places corresponding to elements in
; that is, it has a 1 at the places corresponding to elements in 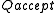 , and a zero otherwise. This vector may be contracted with the internal state probability, to form a scalar
, and a zero otherwise. This vector may be contracted with the internal state probability, to form a scalar
. The language recognized by a specific automaton is then defined as
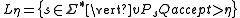
where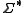 is the set of all strings
is the set of all strings
in the alphabet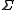 (so that * is the Kleene star
(so that * is the Kleene star
). The language depends on the value of the cut-point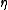 , normally taken to be in the range
, normally taken to be in the range  .
.
A language is called η-stochastic if and only if there exists some PA that recognizes the language, for fixed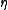 . A language is called stochastic if and only if there is some
. A language is called stochastic if and only if there is some  for which
for which 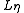 is η-stochastic.
is η-stochastic.
A cut-point is said to be an isolated cut-point if and only if there exists a such that
such that
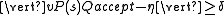
for all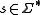
is stochastic, and more strongly, every regular language is η-stochastic. A weak converse is that every 0-stochastic language is regular; however, the general converse does not hold: there are stochastic languages that are not regular.
Every η-stochastic language is stochastic, for some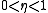 .
.
Every stochastic language is representable by a Rabin automaton.
If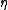 is an isolated cut-point, then
is an isolated cut-point, then  is a regular language.
is a regular language.
 such that
such that
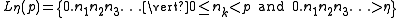
That is, a p-adic language is merely the set of real numbers, written in base-p, such that they are greater than . It is straightforward to show that all p-adic languages are stochastic. However, a p-adic language is regular if and only if
. It is straightforward to show that all p-adic languages are stochastic. However, a p-adic language is regular if and only if 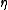 is rational. In particular, this implies that the number of stochastic languages is uncountable.
is rational. In particular, this implies that the number of stochastic languages is uncountable.
, opposite to the orthogonal corner. The transition matrices form a monoid
, acting on the point. This may be generalized by having the point be from some general topological space
, while the transition matrices are chosen from a collection of operators acting on the topological space, thus forming a semiautomaton
. When the cut-point is suitably generalized, one has a topological automaton.
An example of such a generalization is the quantum finite automaton; here, the automaton state is represented by a point in complex projective space
, while the transition matrices are a fixed set chosen from the unitary group
. The cut-point is understood as a limit on the maximum value of the quantum angle.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computer science
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the probabilistic automaton (PA) is a generalization of the non-deterministic finite automaton; it includes the probability of a given transition into the transition function
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
, turning it into a transition matrix or stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
. Thus, the probabilistic automaton generalizes the concept of a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
or subshift of finite type
Subshift of finite type
In mathematics, subshifts of finite type are used to model dynamical systems, and in particular are the objects of study in symbolic dynamics and ergodic theory. They also describe the set of all possible sequences executed by a finite state machine...
. The languages
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
recognized by probabilistic automata are called stochastic languages; these include the regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s as a subset. The number of stochastic languages is uncountable.
The concept was introduced by Michael O. Rabin
Michael O. Rabin
Michael Oser Rabin , is an Israeli computer scientist and a recipient of the Turing Award.- Biography :Rabin was born in 1931 in Breslau, Germany, , the son of a rabbi. In 1935, he emigrated with his family to Mandate Palestine...
in 1963; a certain special case is sometimes known as the Rabin automaton. In recent years, a variant has been formulated in terms of quantum probabilities, the quantum finite automaton.
Definition
The probabilistic automaton may be defined as an extension of a non-deterministic finite automaton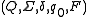 , together with two probabilities: the probability
, together with two probabilities: the probability 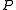 of a particular state transition taking place, and with the initial state
of a particular state transition taking place, and with the initial state 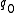 replaced by a stochastic vector giving the probability of the automaton being in a given initial state.
replaced by a stochastic vector giving the probability of the automaton being in a given initial state.For the ordinary non-deterministic finite automaton, one has
- a finite set of states
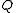
- a finite set of input symbols

- a transition function
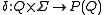
- a set of states
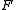 distinguished as accepting (or final) states
distinguished as accepting (or final) states 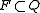 .
.
Here,
 denotes the power set of
denotes the power set of  .
.By use of currying
Currying
In mathematics and computer science, currying is the technique of transforming a function that takes multiple arguments in such a way that it can be called as a chain of functions each with a single argument...
, the transition function
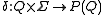 of a non-deterministic finite automaton can be written as a membership function
of a non-deterministic finite automaton can be written as a membership function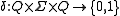
so that
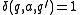 if
if 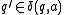 and
and  if
if 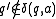 . The curried transition function can be understood to be a matrix with matrix entries
. The curried transition function can be understood to be a matrix with matrix entries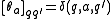
The matrix
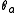 is then a square matrix, whose entries are zero or one, indicating whether a transition
is then a square matrix, whose entries are zero or one, indicating whether a transition 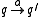 is allowed by the NFA. Such a transition matrix is always defined for a non-deterministic finite automaton.
is allowed by the NFA. Such a transition matrix is always defined for a non-deterministic finite automaton.The probabilistic automaton replaces this matrix by a stochastic matrix
Stochastic matrix
In mathematics, a stochastic matrix is a matrix used to describe the transitions of a Markov chain. It has found use in probability theory, statistics and linear algebra, as well as computer science...
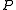 , so that the probability of a transition is given by
, so that the probability of a transition is given by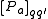
A state change from some state to any state must occur with probability one, of course, and so one must have
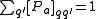
for all input letters
 and internal states
and internal states 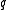 . The initial state of a probabilistic automaton is given by a row vector
. The initial state of a probabilistic automaton is given by a row vector  , whose components add to unity:
, whose components add to unity: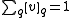
The transition matrix acts on the right, so that the state of the probabilistic automaton, after consuming the input string
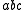 , would be
, would be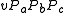
In particular, the state of a probabilistic automaton is always a stochastic vector, since the product of any two stochastic matrices is a stochastic matrix, and the product of a stochastic vector and a stochastic matrix is again a stochastic vector. This vector is sometimes called the distribution of states, emphasizing that it is a discrete probability distribution.
Formally, the definition of a probabilistic automaton does not require the mechanics of the non-deterministic automaton, which may be dispensed with. Formally, a probabilistic automaton PA is defined as the tuple
 . A Rabin automaton is one for which the initial distribution
. A Rabin automaton is one for which the initial distribution  is a coordinate vector
is a coordinate vectorCoordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
; that is, has zero for all but one entries, and the remaining entry being one.
Stochastic languages
The set of languagesFormal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
recognized by probabilistic automata are called stochastic languages. They include the regular language
Regular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
s as a subset.
Let
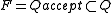 be the set of "accepting" or "final" states of the automaton. By abuse of notation,
be the set of "accepting" or "final" states of the automaton. By abuse of notation, 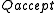 can also be understood to be the column vector that is the membership function for
can also be understood to be the column vector that is the membership function for 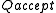 ; that is, it has a 1 at the places corresponding to elements in
; that is, it has a 1 at the places corresponding to elements in 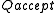 , and a zero otherwise. This vector may be contracted with the internal state probability, to form a scalar
, and a zero otherwise. This vector may be contracted with the internal state probability, to form a scalarScalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
. The language recognized by a specific automaton is then defined as
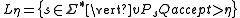
where
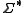 is the set of all strings
is the set of all stringsString (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
in the alphabet
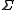 (so that * is the Kleene star
(so that * is the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
). The language depends on the value of the cut-point
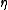 , normally taken to be in the range
, normally taken to be in the range  .
.A language is called η-stochastic if and only if there exists some PA that recognizes the language, for fixed
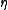 . A language is called stochastic if and only if there is some
. A language is called stochastic if and only if there is some  for which
for which 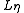 is η-stochastic.
is η-stochastic.A cut-point is said to be an isolated cut-point if and only if there exists a
 such that
such that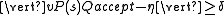
for all
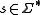
Properties
Every regular languageRegular language
In theoretical computer science and formal language theory, a regular language is a formal language that can be expressed using regular expression....
is stochastic, and more strongly, every regular language is η-stochastic. A weak converse is that every 0-stochastic language is regular; however, the general converse does not hold: there are stochastic languages that are not regular.
Every η-stochastic language is stochastic, for some
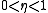 .
.Every stochastic language is representable by a Rabin automaton.
If
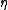 is an isolated cut-point, then
is an isolated cut-point, then  is a regular language.
is a regular language.p-adic languages
The p-adic languages provide an example of a stochastic language that is not regular, and also show that the number of stochastic languages is uncountable. A p-adic language is defined as the set of strings in the letters such that
such that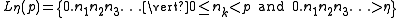
That is, a p-adic language is merely the set of real numbers, written in base-p, such that they are greater than
 . It is straightforward to show that all p-adic languages are stochastic. However, a p-adic language is regular if and only if
. It is straightforward to show that all p-adic languages are stochastic. However, a p-adic language is regular if and only if 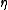 is rational. In particular, this implies that the number of stochastic languages is uncountable.
is rational. In particular, this implies that the number of stochastic languages is uncountable.Generalizations
The probabilistic automaton has a geometric interpretation: the state vector can be understood to be a point that lives on the face of the standard simplexSimplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
, opposite to the orthogonal corner. The transition matrices form a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
, acting on the point. This may be generalized by having the point be from some general topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, while the transition matrices are chosen from a collection of operators acting on the topological space, thus forming a semiautomaton
Semiautomaton
In mathematics and theoretical computer science, a semiautomaton is an automaton having only an input, and no output. It consists of a set Q of states, a set Σ called the input alphabet, and a function T: Q × Σ → Q called the transition function.Associated to any semiautomaton is a monoid called...
. When the cut-point is suitably generalized, one has a topological automaton.
An example of such a generalization is the quantum finite automaton; here, the automaton state is represented by a point in complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, while the transition matrices are a fixed set chosen from the unitary group
Unitary group
In mathematics, the unitary group of degree n, denoted U, is the group of n×n unitary matrices, with the group operation that of matrix multiplication. The unitary group is a subgroup of the general linear group GL...
. The cut-point is understood as a limit on the maximum value of the quantum angle.

