Semiautomaton
Encyclopedia
In mathematics
and theoretical computer science
, a semiautomaton is an automaton
having only an input, and no output. It consists of a set Q of states
, a set Σ called the input alphabet, and a function T: Q × Σ → Q called the transition function.
Associated to any semiautomaton is a monoid
called the characteristic monoid, input monoid, transition monoid or transition system of the semiautomaton, which acts on the set of states Q. This may be viewed either as an action of the free monoid of strings
in the input alphabet Σ, or as the induced transformation semigroup
of Q.
In older books like Clifford and Preston (1967) S-acts are called "operands".
In category theory
, semiautomata essentially are functor
s.
A transformation semigroup or transformation monoid is a pair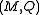
consisting of a set Q (often called the "set of states
") and a semigroup
or monoid
M of functions
, or "transformations", mapping Q to itself. They are functions in the sense that every element m of M is a map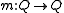
. If s and t are two different elements of the transformation semigroup, then the semigroup product follows trivially from function composition
, so that one defines
as 
.
Some authors regard "semigroup" and "monoid" as synonyms. Here a semigroup need not have an identity element
; a monoid is a semigroup with an identity element. Since the notion of functions acting on a set always includes the notion of an identity function, which when applied to the set does nothing, a transformation semigroup can be made into a monoid by taking its union with the identity function.
and Q be a non-empty set. If there exists a multiplicative operation
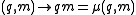
which satisfies the properties
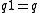
for 1 the unit of the monoid, and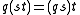
for all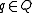
and 
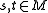, then the triple 
is called a right M-act or simply a right act. In long-hand,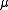 
is the right multiplication of elements of Q by elements of M. The right act is often written as 
.
The left act is defined similarly, with
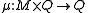
and is often denoted as
.
An M-act is closely related to a transformation monoid. However the elements of M need not be functions per se, they are just elements of some monoid. Therefore, one must demand that the action of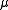
be consistent with multiplication in the monoid (i.e. 
), as, in general, this might not hold for some arbitrary 
, in the way that it does for function composition.
Once one makes this demand, it is completely safe to drop all parenthesis, as the monoid product and the action of the monoid on the set are completely associative. In particular, this allows elements of the monoid to be represented as strings
of letters, in the computer-science sense of the word "string". This abstraction then allows one to talk about string operations in general, and eventually leads to the concept of formal languages as being composed of strings of letters.
Another difference between an M-act and a transformation monoid is that for an M-act Q, two distinct elements of the monoid may determine the same transformation of Q. If we demand that this does not happen, then an M-act is essentially the same as a transformation monoid.
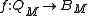
such that
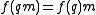
for all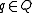
and 
. The set of all M-homomorphisms is commonly written as 
or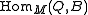 
.
The M-acts and M-homomorphisms together form a category
called M-Act.
where 
is a non-empty set, called the input alphabet, Q is a non-empty set, called the set of states, and T is the transition function
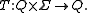
When the set of states Q is a finite set (it need not be!), a semiautomaton may be thought of as a deterministic finite automaton
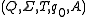, but without the initial state 
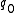or set of accept states A. Alternately, it is a finite state machine
which has no output, and only an input.
Any semiautomaton induces an act of a monoid in the following way.
Let
be the free monoid generated by the alphabet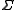 
(so that the superscript * is understood to be the Kleene star
); it is the set of all finite-length strings
composed of the letters in
.
For every word w in
, let 
be the function, defined recursively, as follows, for all q in Q:
Let
be the set
The set
is closed under function composition
; that is, for all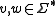
, one has 
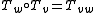. It also contains 
, which is the identity function
on S. Since function composition is associative, the set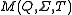
is a monoid: it is called the input monoid, characteristic monoid, characteristic semigroup or transition monoid of the semiautomaton 
.
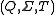s. The construction of all possible transitions driven by strings in the free group has a graphical depiction as de Bruijn graph
s.
The set of states Q need not be finite, or even countable. As an example, semiautomata underpin the concept of quantum finite automata
. There, the set of states Q are given by the complex projective space
, and individual states are referred to as n-state qubit
s. State transitions are given by unitary n×n matrices. The input alphabet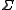
remains finite, and other typical concerns of automata theory remain in play. Thus, the quantum semiautomaton may be simply defined as the triple 
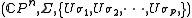when the alphabet 
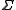has p letters, so that there is one unitary matrix 
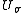for each letter 
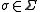. Stated in this way, it is obvious that the quantum semiautomaton has many geometrical generalizations. Thus, for example, one may take a Riemannian symmetric space
in place of
, and selections from its group of isometries as transition functions.
The syntactic monoid
of a formal language
is isomorphic
to the transition monoid of the minimal automaton accepting the language.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and theoretical computer science
Theoretical computer science
Theoretical computer science is a division or subset of general computer science and mathematics which focuses on more abstract or mathematical aspects of computing....
, a semiautomaton is an automaton
Deterministic finite state machine
In the theory of computation and automata theory, a deterministic finite state machine—also known as deterministic finite automaton —is a finite state machine accepting finite strings of symbols. For each state, there is a transition arrow leading out to a next state for each symbol...
having only an input, and no output. It consists of a set Q of states
State (computer science)
In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
, a set Σ called the input alphabet, and a function T: Q × Σ → Q called the transition function.
Associated to any semiautomaton is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
called the characteristic monoid, input monoid, transition monoid or transition system of the semiautomaton, which acts on the set of states Q. This may be viewed either as an action of the free monoid of strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
in the input alphabet Σ, or as the induced transformation semigroup
Transformation semigroup
In algebra and theoretical computer science, an action or act of a semigroup on a set is a rule which associates to each element of the semigroup a transformation of the set in such a way that the product of two elements of the semigroup is associated with the composite of the two corresponding...
of Q.
In older books like Clifford and Preston (1967) S-acts are called "operands".
In category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, semiautomata essentially are functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s.
Transformation semigroups and monoid acts
A transformation semigroup or transformation monoid is a pair
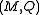consisting of a set Q (often called the "set of statesState (computer science)
In computer science and automata theory, a state is a unique configuration of information in a program or machine. It is a concept that occasionally extends into some forms of systems programming such as lexers and parsers....
") and a semigroup
Semigroup
In mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
or monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
M of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
, or "transformations", mapping Q to itself. They are functions in the sense that every element m of M is a map
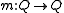. If s and t are two different elements of the transformation semigroup, then the semigroup product follows trivially from function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
, so that one defines
as .Some authors regard "semigroup" and "monoid" as synonyms. Here a semigroup need not have an identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
; a monoid is a semigroup with an identity element. Since the notion of functions acting on a set always includes the notion of an identity function, which when applied to the set does nothing, a transformation semigroup can be made into a monoid by taking its union with the identity function.
M-acts
Let M be a monoidMonoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
and Q be a non-empty set. If there exists a multiplicative operation
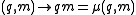
which satisfies the properties
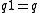
for 1 the unit of the monoid, and
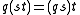
for all
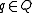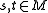and , then the triple is called a right M-act or simply a right act. In long-hand, 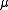is the right multiplication of elements of Q by elements of M. The right act is often written as .The left act is defined similarly, with
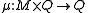
and is often denoted as
.An M-act is closely related to a transformation monoid. However the elements of M need not be functions per se, they are just elements of some monoid. Therefore, one must demand that the action of
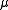be consistent with multiplication in the monoid (i.e. ), as, in general, this might not hold for some arbitrary , in the way that it does for function composition.Once one makes this demand, it is completely safe to drop all parenthesis, as the monoid product and the action of the monoid on the set are completely associative. In particular, this allows elements of the monoid to be represented as strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
of letters, in the computer-science sense of the word "string". This abstraction then allows one to talk about string operations in general, and eventually leads to the concept of formal languages as being composed of strings of letters.
Another difference between an M-act and a transformation monoid is that for an M-act Q, two distinct elements of the monoid may determine the same transformation of Q. If we demand that this does not happen, then an M-act is essentially the same as a transformation monoid.
M-homomorphism
An M-homomorphism is a map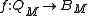such that
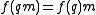
for all
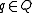and . The set of all M-homomorphisms is commonly written as or 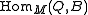.The M-acts and M-homomorphisms together form a category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
called M-Act.
Semiautomata
A semiautomaton is a triple where is a non-empty set, called the input alphabet, Q is a non-empty set, called the set of states, and T is the transition function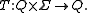When the set of states Q is a finite set (it need not be!), a semiautomaton may be thought of as a deterministic finite automaton
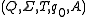, but without the initial state 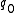or set of accept states A. Alternately, it is a finite state machineFinite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
which has no output, and only an input.
Any semiautomaton induces an act of a monoid in the following way.
Let
be the free monoid generated by the alphabet 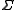(so that the superscript * is understood to be the Kleene starKleene star
In mathematical logic and computer science, the Kleene star is a unary operation, either on sets of strings or on sets of symbols or characters. The application of the Kleene star to a set V is written as V*...
); it is the set of all finite-length strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
composed of the letters in
.For every word w in
, let be the function, defined recursively, as follows, for all q in Q:- If
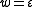, then 
, so that the empty word 
does not change the state.
- If
is a letter in 
, then 
.
- If
for 
and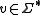 
, then 
.
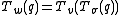Let
be the setThe set
is closed under function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
; that is, for all
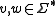, one has 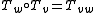. It also contains , which is the identity functionIdentity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
on S. Since function composition is associative, the set
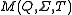is a monoid: it is called the input monoid, characteristic monoid, characteristic semigroup or transition monoid of the semiautomaton 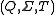.Properties
If the set of states Q is finite, then the transition functions are commonly represented as state transition tableState transition table
In automata theory and sequential logic, a state transition table is a table showing what state a finite semiautomaton or finite state machine will move to, based on the current state and other inputs...
s. The construction of all possible transitions driven by strings in the free group has a graphical depiction as de Bruijn graph
De Bruijn graph
In graph theory, an n-dimensional De Bruijn graph of m symbols is a directed graph representing overlaps between sequences of symbols. It has mn vertices, consisting of all possible length-n sequences of the given symbols; the same symbol may appear multiple times in a sequence...
s.
The set of states Q need not be finite, or even countable. As an example, semiautomata underpin the concept of quantum finite automata
Quantum finite automata
In quantum computing, quantum finite automata or QFA are a quantum analog of probabilistic automata. They are related to quantum computers in a similar fashion as finite automata are related to Turing machines. Several types of automata may be defined, including measure-once and measure-many automata...
. There, the set of states Q are given by the complex projective space
Complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a complex projective space label the complex lines...
, and individual states are referred to as n-state qubitQubit
In quantum computing, a qubit or quantum bit is a unit of quantum information—the quantum analogue of the classical bit—with additional dimensions associated to the quantum properties of a physical atom....
s. State transitions are given by unitary n×n matrices. The input alphabet
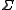remains finite, and other typical concerns of automata theory remain in play. Thus, the quantum semiautomaton may be simply defined as the triple 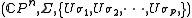when the alphabet 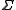has p letters, so that there is one unitary matrix 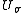for each letter 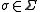. Stated in this way, it is obvious that the quantum semiautomaton has many geometrical generalizations. Thus, for example, one may take a Riemannian symmetric spaceRiemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
in place of
, and selections from its group of isometries as transition functions.The syntactic monoid
Syntactic monoid
In mathematics and computer science, the syntactic monoid M of a formal language L is the smallest monoid that recognizes the language L.-Syntactic quotient:...
of a formal language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
is isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to the transition monoid of the minimal automaton accepting the language.