Reconstruction conjecture
Encyclopedia
Informally, the reconstruction conjecture in graph theory
says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
, a vertex-deleted subgraph of 
is a subgraph formed by deleting exactly one vertex from 
. Clearly, it is an induced subgraph of 
.
For a graph
, the deck of G, denoted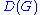 
, is the multiset
of all vertex-deleted subgraphs of
. Each graph in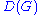 
is called a card. Two graphs that have the same deck are said to be hypomorphic.
With these definitions, the conjecture can be stated as:
Reconstruction Conjecture: Any two hypomorphic graphs on at least three vertices are isomorphic.
(The requirement that the graphs have at least three vertices is necessary because both graphs on two vertices have the same decks.)
Harary
suggested a stronger version of the conjecture:
Set Reconstruction Conjecture: Any two graphs on at least four vertices with the same sets of vertex-deleted subgraphs are isomorphic.
Given a graph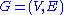
, an edge-deleted subgraph of 
is a subgraph formed by deleting exactly one edge from 
.
For a graph
, the edge-deck of G, denoted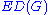 
, is the multiset
of all edge-deleted subgraphs of
. Each graph in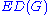 
is called an edge-card.
Edge Reconstruction Conjecture: (Harary, 1964) Any two graphs with at least four edges and having the same edge-decks are isomorphic.
).
In a probabilistic sense, it has been shown (Bollobás
) that almost all graphs are reconstructible. This means that the probability that a randomly chosen graph on
vertices is not reconstructible goes to 0 as 
goes to infinity. In fact, it was shown that not only are almost all graphs reconstructible, but in fact that the entire deck is not necessary to reconstruct them — almost all graphs have the property that there exist three cards in their deck that uniquely determine the graph.
is called recognizable if one can determine the property from the deck of a graph. The following properties of graphs are recognizable:
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
says that graphs are determined uniquely by their subgraphs. It is due to Kelly and Ulam.
Formal statements
Given a graph, a vertex-deleted subgraph of is a subgraph formed by deleting exactly one vertex from . Clearly, it is an induced subgraph of .For a graph
, the deck of G, denoted 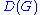, is the multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of all vertex-deleted subgraphs of
. Each graph in 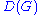is called a card. Two graphs that have the same deck are said to be hypomorphic.With these definitions, the conjecture can be stated as:
Reconstruction Conjecture: Any two hypomorphic graphs on at least three vertices are isomorphic.
(The requirement that the graphs have at least three vertices is necessary because both graphs on two vertices have the same decks.)
Harary
Frank Harary
Frank Harary was a prolific American mathematician, who specialized in graph theory. He was widely recognized as one of the "fathers" of modern graph theory....
suggested a stronger version of the conjecture:
Set Reconstruction Conjecture: Any two graphs on at least four vertices with the same sets of vertex-deleted subgraphs are isomorphic.
Given a graph
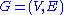, an edge-deleted subgraph of is a subgraph formed by deleting exactly one edge from .For a graph
, the edge-deck of G, denoted 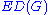, is the multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
of all edge-deleted subgraphs of
. Each graph in 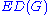is called an edge-card.Edge Reconstruction Conjecture: (Harary, 1964) Any two graphs with at least four edges and having the same edge-decks are isomorphic.
Verification
Both the reconstruction and set reconstruction conjectures have been verified for all graphs with at most 11 vertices (McKayBrendan McKay
Brendan Damien McKay is a Professor in the Research School of Computer Science at the Australian National University . He has published extensively in combinatorics....
).
In a probabilistic sense, it has been shown (Bollobás
Béla Bollobás
Béla Bollobás FRS is a Hungarian-born British mathematician who has worked in various areas of mathematics, including functional analysis, combinatorics, graph theory and percolation. As a student, he took part in the first three International Mathematical Olympiads, winning two gold medals...
) that almost all graphs are reconstructible. This means that the probability that a randomly chosen graph on
vertices is not reconstructible goes to 0 as goes to infinity. In fact, it was shown that not only are almost all graphs reconstructible, but in fact that the entire deck is not necessary to reconstruct them — almost all graphs have the property that there exist three cards in their deck that uniquely determine the graph.Reconstructible graph families
The conjecture has been verified for a number of infinite classes of graphs.- Regular graphRegular graphIn graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...
s - TreesTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
- Disconnected graphs
- Unit interval graphs
- Separable graphs without end vertices
- Maximal Planar Graphs
- Maximal Outerplanar Graphs
- Outer Planar Graphs
- Critical blocks
Recognizable properties
In context of the reconstruction conjecture, a graph propertyGraph property
In graph theory, a graph property or graph invariant is a property of graphs that depends only on the abstract structure, not on graph representations such as particular labellings or drawings of the graph.-Definitions:...
is called recognizable if one can determine the property from the deck of a graph. The following properties of graphs are recognizable:
- Degree sequence
- Tutte polynomialTutte polynomialThe Tutte polynomial, also called the dichromate or the Tutte–Whitney polynomial, is a polynomial in two variables which plays an important role in graph theory, a branch of mathematics and theoretical computer science...
- PlanarityPlanar graphIn graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
- The types of spanning treeSpanning tree (mathematics)In the mathematical field of graph theory, a spanning tree T of a connected, undirected graph G is a tree composed of all the vertices and some of the edges of G. Informally, a spanning tree of G is a selection of edges of G that form a tree spanning every vertex...
s in a graph - Chromatic polynomialChromatic polynomialThe chromatic polynomial is a polynomial studied in algebraic graph theory, a branch of mathematics. It counts the number of graph colorings as a function of the number of colors and was originally defined by George David Birkhoff to attack the four color problem. It was generalised to the Tutte...
- Being a perfect graphPerfect graphIn graph theory, a perfect graph is a graph in which the chromatic number of every induced subgraph equals the size of the largest clique of that subgraph....
or an interval graphInterval graphIn graph theory, an interval graph is the intersection graph of a multiset of intervals on the real line. It has one vertex for each interval in the set, and an edge between every pair of vertices corresponding to intervals that intersect.-Definition:...
, or some other subclasses of perfect graphs
Other structures
It has been shown that the following are not in general reconstructible:- Digraphs: Infinite families of non-reconstructible digraphs are known, including tournaments (Stockmeyer) and non-tournaments (Stockmeyer). A tournament is reconstructible if it is not strongly connected.
- HypergraphHypergraphIn mathematics, a hypergraph is a generalization of a graph, where an edge can connect any number of vertices. Formally, a hypergraph H is a pair H = where X is a set of elements, called nodes or vertices, and E is a set of non-empty subsets of X called hyperedges or links...
s (KocayWilliam Lawrence KocayWilliam Lawrence Kocay is a Canadian professor at the department of computer science at St. Paul's College of the University of Manitoba and a graph theorist. He is known for his work in graph algorithms and the reconstruction conjecture and is affectionately referred to as "Wild Bill *pew-pew*" by...
). - Infinite graphs. Let T be a tree on an infinite number of vertices such that every vertex has infinite degree. The counterexample is T and 2T. The question of reconstructibility for locally finite infinite graphs is still open.
Further reading
For further information on this topic, see the survey by Nash-WilliamsCrispin St. J. A. Nash-Williams
Crispin St. John Alvah Nash-Williams was a British and Canadian mathematician. His research interest was in the field of discrete mathematics, especially graph theory....
.