Regular Polytopes is a mathematical

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 geometry

Geometry

Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....

 book written by Canadian

Canada

Canada is a North American country consisting of ten provinces and three territories. Located in the northern part of the continent, it extends from the Atlantic Ocean in the east to the Pacific Ocean in the west, and northward into the Arctic Ocean...

 mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

 H.S.M. Coxeter. Originally written in 1947, the book was updated and republished in 1963 and 1973.

The book is a comprehensive survey of the geometry of regular polytope

Regular polytope

In mathematics, a regular polytope is a polytope whose symmetry is transitive on its flags, thus giving it the highest degree of symmetry. All its elements or j-faces — cells, faces and so on — are also transitive on the symmetries of the polytope, and are regular polytopes of...

s, the generalisation of regular polygon

Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

s and regular polyhedra

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 to higher dimensions. Originating with an essay entitled Dimensional Analogy written in 1923, the first edition of the book took Coxeter 24 years to complete.

Scope

Coxeter starts by introducing two-dimensional polygons and three-dimensional polyhedra. He then gives a rigorous combinatorial definition of "regularity" and uses it to show that there are no other convex regular polyhedra apart from the five Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s. The concept of "regularity" is extended to non-convex shapes such as star polygons and star polyhedra

Star polyhedron

In geometry, a star polyhedron is a polyhedron which has some repetitive quality of nonconvexity giving it a star-like visual quality.There are two general kinds of star polyhedron:*Polyhedra which self-intersect in a repetitive way....

; to tessellation

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

s and honeycomb

Honeycomb

A honeycomb is a mass of hexagonal waxcells built by honey bees in their nests to contain their larvae and stores of honey and pollen.Beekeepers may remove the entire honeycomb to harvest honey...

s and to polytopes in higher dimensions. Coxeter introduces and uses the groups of reflections that became known as Coxeter group

Coxeter group

In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...

s.

The book combines algebraic rigour with clear explanations, many of which are illustrated with diagrams, and with a diagramatic notation for Wythoff construction

Wythoff construction

In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...

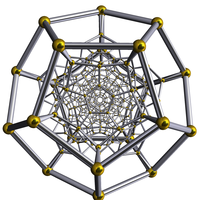
s. The black and white plates in the book show solid models of three-dimensional polyhedra, and wire-frame models of projections of some higher-dimensional polytopes. At the end of each chapter Coxeter includes an "Historical remarks" section which provides an historical perspective of the development of the subject.

Importance

Regular Polytopes is a standard reference work on regular polygons, polyhedra and their higher dimensional analogues. It is unusual in the breadth of its coverage; its combination of mathematical rigour with geometric insight; and the clarity of its diagrams and illustrations.

In a brief review of the 1963 Dover reprint in MathSciNet an anonymous reviewer writes that “anyone interested in the relationship of group theory to geometry should own a copy.” The original 1948 edition received a more complete review by M. Goldberg in , and the third edition was reviewed telegraphically in .