Relations between Fourier transforms and Fourier series

In the mathematical field of harmonic analysis

Harmonic analysis

Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...

, the continuous Fourier transform

Continuous Fourier transform

The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...

has very precise relations with Fourier series

Fourier series

In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

. It is also closely related to the discrete-time Fourier transform

Discrete-time Fourier transform

In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...

(DTFT) and the discrete Fourier transform

Discrete Fourier transform

In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...

(DFT).

The Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

can be applied to time-discrete or time-periodic signals using the δ-Dirac

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

formalism. In fact the Fourier series, the DTFT and the DFT can be derived all from the general continuous Fourier transform. They are, from a theoretical point of view, particular cases of the Fourier transform.

In signal theory and digital signal processing

Digital signal processing

Digital signal processing is concerned with the representation of discrete time signals by a sequence of numbers or symbols and the processing of these signals. Digital signal processing and analog signal processing are subfields of signal processing...

(DSP), the DFT (implemented as fast Fourier transform

Fast Fourier transform

A fast Fourier transform is an efficient algorithm to compute the discrete Fourier transform and its inverse. "The FFT has been called the most important numerical algorithm of our lifetime ." There are many distinct FFT algorithms involving a wide range of mathematics, from simple...

) is extensively used to calculate approximations to the spectrum of a continuous signal, knowing only a sequence of sampled points. The relations between DFT and Fourier transform are in this case essential.

Definitions

In the following table the definitions for the continuous Fourier transform, Fourier series, DTFT and DFT are reported:

Fourier transformations definitions
×	Continuous time	Discrete time
Time aperiodic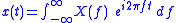
-
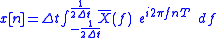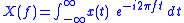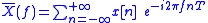Time periodic
-

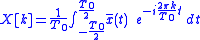The table shows the properties of the time-domain signal:

Continuous time versus Discrete Time (columns),

Aperiodic in time versus Periodic in time (rows).

Equations needed to relate the various transformations

The definitions given in the previous section can be introduced axiomatically or can be derived from the continuous Fourier transform

Continuous Fourier transform

using the extend formalism of Dirac delta. Using this formalism the Continuous Fourier transform can be applied also to discrete or periodic signals.

To calculate the continuous Fourier transform of discrete and/or periodic signals we need to introduce some equations and recall some Fourier transform properties. Here is reported a list of them:

1. The first Poisson summation formula

Poisson summation formula

In mathematics, the Poisson summation formula is an equation that relates the Fourier series coefficients of the periodic summation of a function to values of the function's continuous Fourier transform. Consequently, the periodic summation of a function is completely defined by discrete samples...

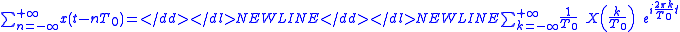
2. The second Poisson summation formula

Poisson summation formula

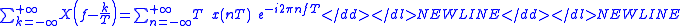
3. The Dirac comb

Dirac comb

In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...

transform is important to understand the link between the continuous and the discrete or periodic case:

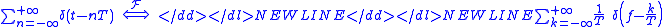
4. The theorems which define the Fourier transform properties, in particular the convolution property.

All these equations and properties can be demonstrated on their own.

Once calculated, the continuous Fourier transform of discrete and/or periodic signals can be related to the DTFT, the Fourier series and to the DFT definitions given above.

Relationship between the various transforms

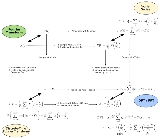
The following figure depicts the relations between the various transforms.

Explanation of the symbols: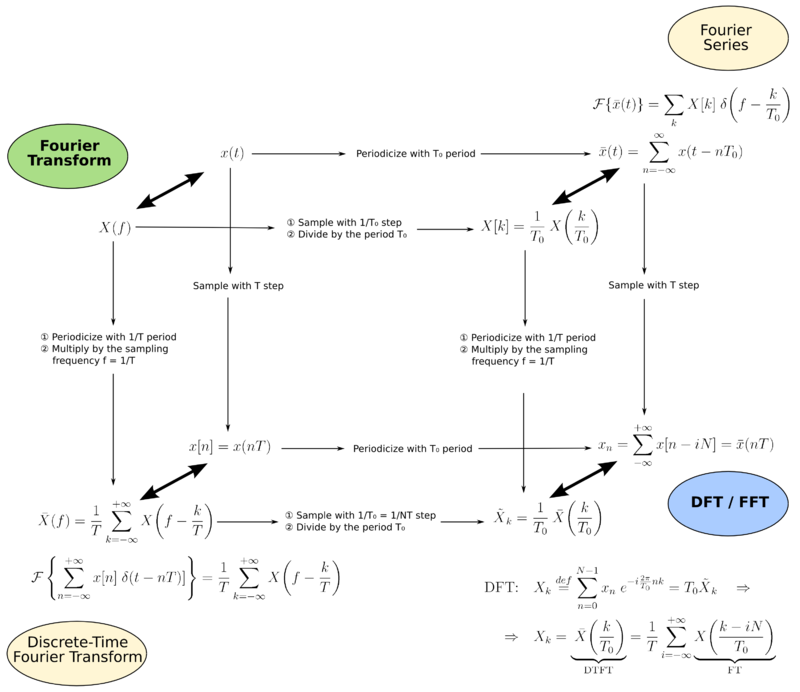

The signal and its transform are bound by a bold double arrow ().
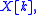and 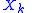are infinite sequences.
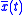and 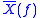are periodic functions.
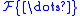indicates exclusively the continuous Fourier transform.

The Poisson summation formulas allow us to link the Fourier series and the DTFT to the Fourier transform (respectively formulas 1. and 2.).

The convolution property (4.) and Dirac comb transform (3.) allow us to calculate the Fourier transform for the time-periodic or time-discrete signals in terms of X(ƒ). Figure 2 shows which operations correspond, in the spectral domain, to the sampling of a continuous signal or to the periodic summation of an aperiodic signal.

From Figure 2 we can see that the time domain sampling has the same effect on the spectrum both for an aperiodic signal (x(t)) and for a periodic signal (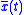

). Conversely, the time domain periodic summation has the same spectral effect on a continuous signal (x(t)) and on a discrete signal (x[n]).

Fourier series

Since any periodic function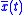

can be modelled as a periodic summation of an aperiodic function, x(t):

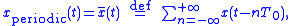
the first Poisson summation formula becomes:

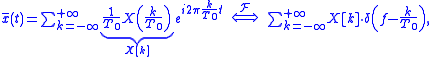
which is also known as a Fourier series

Fourier series

In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

with coefficients X[k].

This shows is that the frequency distribution of a periodic function is not spread over a continuum range of frequency. Rather it is concentrated in discrete, equally spaced, frequency values, which are all multiples of 1/T₀, called the fundamental frequency
Fundamental frequency
The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the lowest frequency of a periodic waveform. In terms of a superposition of sinusoids The fundamental frequency, often referred to simply as the fundamental and abbreviated f0, is defined as the...

. Figure 2 indicates this relationship via the horizontal arrows that go from x(t) to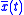 and from X(ƒ) to X[k].

It can be shown that the coefficients can be determined from just one cycle of 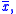as follows:

where

is the integral over any interval of length T_0..

Since the coefficients are samples of X(ƒ), they can provide useful insight into an aperiodic function, x(t), in lieu of the continuous transform. And if x(t) has finite duration (compact support), and T₀ is sufficiently long, x(t) can be recovered from the Fourier series ().

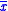Discrete-time Fourier transform (DTFT)

When a function of a discrete variable (x[n] for integer values of n) represents samples at some time-interval (T) of function x(t), the second Poisson summation formula indicates that the samples can be used to gain insight into X(ƒ) and possibly even recover both X(ƒ) and x(t):

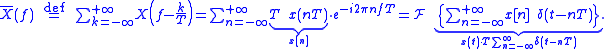
Thus the DTFT of the x[n] sequence is also the Fourier transform of the modulated Dirac comb
Dirac comb
In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...

function. Consequently, a common and useful practice is to model "sampling" as a multiplication by the Dirac comb
Dirac comb
In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...

function, which of course is only "possible" in a purely mathematical sense. But it is sometimes used as a proof of the Poisson summation formula.Here we apply the convolution theorem to the product of two functions: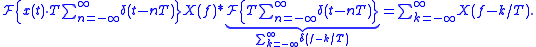

Our interest in 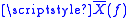is often two-fold: Besides whatever it can tell us about X(ƒ), it also provides insight into the amount of aliasing
Aliasing
In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...

caused by the sampling process.

In Figure 2 the DTFT formulae are displayed in the lower left corner, and the vertical arrows that go from x(t) to x[n] and from X(ƒ) to 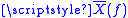indicate the cause/effect relationship of sampling in one domain and periodic summation in the other.

Discrete Fourier Transform (DFT)

The DTFT of a periodic sequence,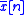

, with period N, becomes another Dirac comb

Dirac comb

In mathematics, a Dirac comb is a periodic Schwartz distribution constructed from Dirac delta functions...

function, modulated by the coefficients of a Fourier series, and the integral formula for the coefficients simplifies to a summation:

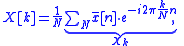where

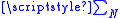is the sum over any n-sequence of length N.

The X_k sequence is what's customarily known as the DFT of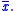

It is also N-periodic, so it is never necessary to compute more than N coefficients. In terms of X_k, the inverse transform is given by:

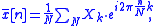where

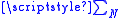is the sum over any k-sequence of length N.

When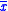

is expressed as a periodic summation of another function, x[n] = T·x(nT):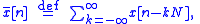

the coefficients are equivalent to samples of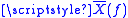

at discrete intervals of 1/NT: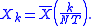

In most cases, N is chosen equal to the length of non-zero portion of x[n]. Increasing N, known as zero-padding or interpolation, results in more closely spaced samples of one period of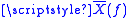

. Decreasing N, causes overlap (adding) in the time-domain (analogous to aliasing

Aliasing

In signal processing and related disciplines, aliasing refers to an effect that causes different signals to become indistinguishable when sampled...

), which corresponds to decimation in the frequency domain. (see Sampling the DTFT) In most cases of practical interest, the x[n] sequence represents a longer sequence that was truncated by the application of a finite-length window function

Window function

In signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...

or FIR filter array.

Definitions

Equations needed to relate the various transformations

Relationship between the various transforms

Fourier series

Discrete-time Fourier transform (DTFT)

Discrete Fourier Transform (DFT)

See also