Resource bounded measure
Encyclopedia
Lutz's resource bounded measure is a generalisation of Lebesgue measure
to complexity class
es. It was originally developed by Jack Lutz
. Just as Lebesgue measure gives a method to quantify the size of subsets of the Euclidean space
, resource bounded measure gives a method to classify the size of subsets of complexity classes.
For instance, computer scientists generally believe that the complexity class P
(the set of all decision problem
s solvable in polynomial time) is not equal to the complexity class NP
(the set of all decision problems checkable, but not necessarily solvable, in polynomial time). Since P is a subset
of NP, this would mean that NP contains more problems than P. A stronger hypothesis than "P is not NP" is the statement "NP does not have p-measure 0". Here, p-measure is a generalization of Lebesgue measure to subsets of the complexity class E
, in which P is contained. P is known to have p-measure 0, and so the hypothesis "NP does not have p-measure 0" would imply not only that NP and P are unequal, but that NP is, in a measure-theoretic sense, "much bigger than P".
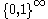is the set of all infinite, binary
sequences. We can view a real number
in the unit interval
as an infinite binary sequence, by considering its binary expansion. We may also view a language
(a set of binary strings
) as an infinite binary sequence, by setting the nth bit
of the sequence to 1 if and only if the nth binary string (in lexicographical order
) is contained in the language. Thus, sets of real numbers in the unit interval and complexity classes (which are sets of languages) may both be viewed as sets of infinite binary sequences, and thus the techniques of measure theory used to measure the size of sets of real numbers may be applied to measure complexity classes. However, since each complexity class contains only a countable number of elements, each complexity class has Lebesgue measure
0. Thus, to do measure theory inside of complexity classes, we must define an alternative measure
that works meaningfully on countable sets of infinite sequences. For this measure to be meaningful, it should reflect something about the underlying definition of each complexity class; namely, that they are defined by computational problem
s that can be solved within a given resource bound.
The foundation of resource-bounded measure is Ville's formulation of martingale
s. A martingale is a function
such that, for all finite strings w,
.
(This is Ville's original definition of a martingale, later extended by Joseph Leo Doob
.) A martingale d is said to succeed on a sequence
if 
where 
is the first n bits of S. A martingale succeeds on a set of sequences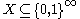 
if it succeeds on every sequence in X.
Intuitively, a martingale is a gambler that starts with some finite amount of money (say, one dollar). It reads a sequence of bits indefinitely. After reading the finite prefix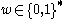
, it bets some of its current money that the next bit will be a 0, and the remainder of its money that the next bit will be a 1. It doubles whatever money was placed on the bit that appears next, and it loses the money placed on the bit that did not appear. It must bet all of its money, but it may "bet nothing" by placing half of its money on each bit. For a martingale d, d(w) represents the amount of money d has after reading the string w. Although the definition of a martingale has the martingale calculating how much money it will have, rather than calculating what bets to place, because of the constrained nature of the game, knowledge the values d(w), d(w0), and d(w1) suffices to calculate the bets that d placed on 0 and 1 after seeing the string w. The fact that the martingale is a function that takes as input the string seen so far means that the bets placed are solely a function of the bits already read; no other information may affect the bets (other information being the so-called filtration in the generalized theory of martingales
).
The key result relating measure to martingales is Ville's observation that a set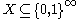
has Lebesgue measure 0 if and only if there is martingale that succeeds on X. Thus, we can define a measure 0 set to be one for which there exists a martingale that succeeds on all elements of the set.
To extend this type of measure to complexity classes, Lutz considered restricting the computational power of the martingale. For instance, if instead of allowing any martingale, we require the martingale to be polynomial-time computable, then we obtain a definition of p-measure: a set of sequences has p-measure 0 if there is a polynomial-time computable martingale that succeeds on the set. We define a set to have p-measure 1 if its complement has p-measure 0. For example, proving the above-mentioned conjecture, that NP does not have p-measure 0, amounts to proving that no polynomial-time martingale succeeds on all of NP.
C if it is in C and "many" other problems in C reduce to it. More specifically, the subset of problems of C which reduce to the problem is a measure one set, in terms of the resource bounded measure. This is a weaker requirement than the problem being complete
for the class.
External links
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
to complexity class
Complexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
es. It was originally developed by Jack Lutz
Jack Lutz
Jack Lutz is a theoretical computer scientist and computational theorist best known for developing the concepts of resource bounded measure and effective dimension. He is currently a professor at Iowa State University.-External links:*...
. Just as Lebesgue measure gives a method to quantify the size of subsets of the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, resource bounded measure gives a method to classify the size of subsets of complexity classes.For instance, computer scientists generally believe that the complexity class P
P
P is the sixteenth letter of the basic modern Latin alphabet.-Usage:In English and most other European languages, P is a voiceless bilabial plosive. Both initial and final Ps can be combined with many other discrete consonants in English words...
(the set of all decision problem
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
s solvable in polynomial time) is not equal to the complexity class NP
NP (complexity)
In computational complexity theory, NP is one of the most fundamental complexity classes.The abbreviation NP refers to "nondeterministic polynomial time."...
(the set of all decision problems checkable, but not necessarily solvable, in polynomial time). Since P is a subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of NP, this would mean that NP contains more problems than P. A stronger hypothesis than "P is not NP" is the statement "NP does not have p-measure 0". Here, p-measure is a generalization of Lebesgue measure to subsets of the complexity class E
E (complexity)
In computational complexity theory, the complexity class E is the set of decision problems that can be solved by a deterministic Turing machine in time 2O and is therefore equal to the complexity class DTIME....
, in which P is contained. P is known to have p-measure 0, and so the hypothesis "NP does not have p-measure 0" would imply not only that NP and P are unequal, but that NP is, in a measure-theoretic sense, "much bigger than P".
Definition
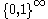is the set of all infinite, binaryBinary numeral system
The binary numeral system, or base-2 number system, represents numeric values using two symbols, 0 and 1. More specifically, the usual base-2 system is a positional notation with a radix of 2...
sequences. We can view a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
as an infinite binary sequence, by considering its binary expansion. We may also view a language
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
(a set of binary strings
String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
) as an infinite binary sequence, by setting the nth bit
Bit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
of the sequence to 1 if and only if the nth binary string (in lexicographical order
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
) is contained in the language. Thus, sets of real numbers in the unit interval and complexity classes (which are sets of languages) may both be viewed as sets of infinite binary sequences, and thus the techniques of measure theory used to measure the size of sets of real numbers may be applied to measure complexity classes. However, since each complexity class contains only a countable number of elements, each complexity class has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0. Thus, to do measure theory inside of complexity classes, we must define an alternative measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
that works meaningfully on countable sets of infinite sequences. For this measure to be meaningful, it should reflect something about the underlying definition of each complexity class; namely, that they are defined by computational problem
Computational problem
In theoretical computer science, a computational problem is a mathematical object representing a collection of questions that computers might want to solve. For example, the problem of factoring...
s that can be solved within a given resource bound.
The foundation of resource-bounded measure is Ville's formulation of martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
s. A martingale is a function
such that, for all finite strings w,.(This is Ville's original definition of a martingale, later extended by Joseph Leo Doob
Joseph Leo Doob
Joseph Leo Doob was an American mathematician, specializing in analysis and probability theory.The theory of martingales was developed by Doob.-Early life and education:...
.) A martingale d is said to succeed on a sequence
if where is the first n bits of S. A martingale succeeds on a set of sequences 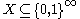if it succeeds on every sequence in X.Intuitively, a martingale is a gambler that starts with some finite amount of money (say, one dollar). It reads a sequence of bits indefinitely. After reading the finite prefix
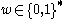, it bets some of its current money that the next bit will be a 0, and the remainder of its money that the next bit will be a 1. It doubles whatever money was placed on the bit that appears next, and it loses the money placed on the bit that did not appear. It must bet all of its money, but it may "bet nothing" by placing half of its money on each bit. For a martingale d, d(w) represents the amount of money d has after reading the string w. Although the definition of a martingale has the martingale calculating how much money it will have, rather than calculating what bets to place, because of the constrained nature of the game, knowledge the values d(w), d(w0), and d(w1) suffices to calculate the bets that d placed on 0 and 1 after seeing the string w. The fact that the martingale is a function that takes as input the string seen so far means that the bets placed are solely a function of the bits already read; no other information may affect the bets (other information being the so-called filtration in the generalized theory of martingalesMartingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
).
The key result relating measure to martingales is Ville's observation that a set
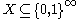has Lebesgue measure 0 if and only if there is martingale that succeeds on X. Thus, we can define a measure 0 set to be one for which there exists a martingale that succeeds on all elements of the set.To extend this type of measure to complexity classes, Lutz considered restricting the computational power of the martingale. For instance, if instead of allowing any martingale, we require the martingale to be polynomial-time computable, then we obtain a definition of p-measure: a set of sequences has p-measure 0 if there is a polynomial-time computable martingale that succeeds on the set. We define a set to have p-measure 1 if its complement has p-measure 0. For example, proving the above-mentioned conjecture, that NP does not have p-measure 0, amounts to proving that no polynomial-time martingale succeeds on all of NP.
Almost complete
A problem is almost complete for a complexity classComplexity class
In computational complexity theory, a complexity class is a set of problems of related resource-based complexity. A typical complexity class has a definition of the form:...
C if it is in C and "many" other problems in C reduce to it. More specifically, the subset of problems of C which reduce to the problem is a measure one set, in terms of the resource bounded measure. This is a weaker requirement than the problem being complete
Complete (complexity)
In computational complexity theory, a computational problem is complete for a complexity class if it is, in a formal sense, one of the "hardest" or "most expressive" problems in the complexity class...
for the class.
External links