In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, SO(5), also denoted SO₅(R) or SO(5,R), is the special orthogonal group of degree 5 over the field R of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s, i.e. (isomorphic to) the group of orthogonal

Orthogonal matrix

In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....

 5×5 matrices

Matrix (mathematics)

In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

 of determinant

Determinant

In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...

 1.

Geometric interpretation

SO(5) is a subgroup of the direct Euclidean group E⁺(5), the group of direct isometries

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

, i.e., isometries preserving orientation

Orientation (mathematics)

In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...

, of R⁵, consisting of elements which leave the origin fixed.

More precisely, we have:

SO(5) 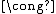E⁺(5) / T

where T is the translational

Translation (geometry)

In Euclidean geometry, a translation moves every point a constant distance in a specified direction. A translation can be described as a rigid motion, other rigid motions include rotations and reflections. A translation can also be interpreted as the addition of a constant vector to every point, or...

 group of R⁵.

See also

• orthogonal matrix
  Orthogonal matrix
  In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
  
  
• orthogonal group
  Orthogonal group
  In mathematics, the orthogonal group of degree n over a field F is the group of n × n orthogonal matrices with entries from F, with the group operation of matrix multiplication...
  
  
• rotation group
  Rotation group
  In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
  
  
• List of simple Lie groups