
SPIKE algorithm
Encyclopedia
The SPIKE algorithm is a hybrid parallel
solver for banded
linear systems developed by Eric Polizzi and Ahmed Sameh.
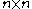 matrix of bandwidth much less than
matrix of bandwidth much less than  , and is an
, and is an 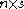 matrix containing
matrix containing  right-hand sides. It is divided into a preprocessing stage and a postprocessing stage.
right-hand sides. It is divided into a preprocessing stage and a postprocessing stage.
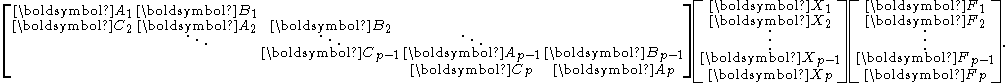
Assume, for the time being, that the diagonal blocks ( with ) are nonsingular. Define a block diagonal matrix
then is also nonsingular. Left-multiplying to both sides of the system gives
Parallel computing
Parallel computing is a form of computation in which many calculations are carried out simultaneously, operating on the principle that large problems can often be divided into smaller ones, which are then solved concurrently . There are several different forms of parallel computing: bit-level,...
solver for banded
Band matrix
In mathematics, particularly matrix theory, a band matrix is a sparse matrix whose non-zero entries are confined to a diagonal band, comprising the main diagonal and zero or more diagonals on either side.-Matrix bandwidth:...
linear systems developed by Eric Polizzi and Ahmed Sameh.
Overview
The SPIKE algorithm deals with a linear system , where is a banded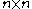 matrix of bandwidth much less than
matrix of bandwidth much less than  , and is an
, and is an 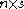 matrix containing
matrix containing  right-hand sides. It is divided into a preprocessing stage and a postprocessing stage.
right-hand sides. It is divided into a preprocessing stage and a postprocessing stage.Preprocessing stage
In the preprocessing stage, the linear system is partitioned into a block tridiagonal form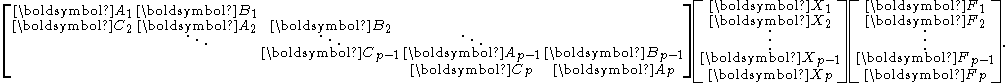
Assume, for the time being, that the diagonal blocks ( with ) are nonsingular. Define a block diagonal matrix
- ,
then is also nonsingular. Left-multiplying to both sides of the system gives
-
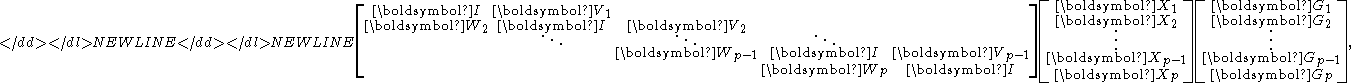
which is to be solved in the postprocessing stage. Left-multiplication by is equivalent to solving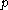 systems of the form
systems of the form
(omitting and for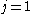 , and and for
, and and for 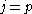 ), which can be carried out in parallel.
), which can be carried out in parallel.
Due to the banded nature of , only a few leftmost columns of each and a few rightmost columns of each can be nonzero. These columns are called the spikes.
Postprocessing stage
Without loss of generalityWithout loss of generalityWithout loss of generality is a frequently used expression in mathematics...
, assume that each spike contains exactly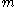 columns (
columns (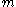 is much less than
is much less than  ) (pad the spike with columns of zeroes if necessary). Partition the spikes in all and into
) (pad the spike with columns of zeroes if necessary). Partition the spikes in all and into
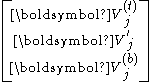 and
and 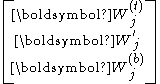
where , , and are of dimensions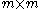 . Partition similarly all and into
. Partition similarly all and into
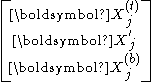 and
and 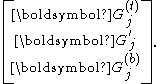
Notice that the system produced by the preprocessing stage can be reduced to a block pentadiagonalPentadiagonal matrixIn linear algebra, a pentadiagonal matrix is a matrix that is nearly diagonal; to be exact, it is a matrix in which the only nonzero entries are on the main diagonal, and the first two diagonals above and below it...
system of much smaller size (recall that is much less than
is much less than  )
)
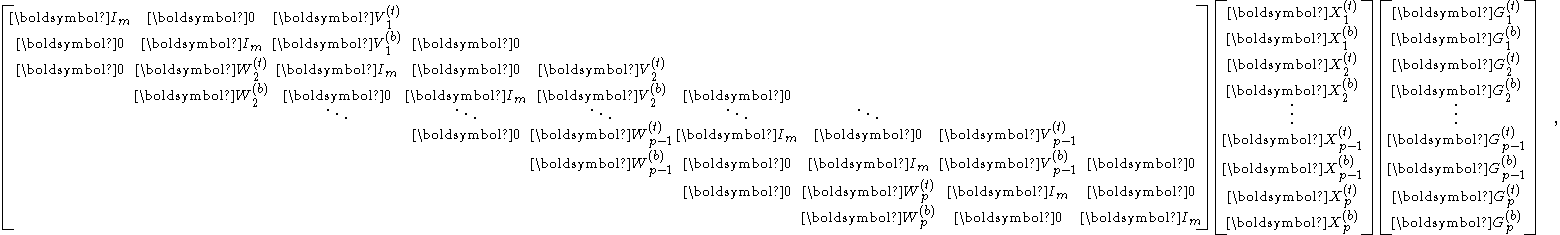
which we call the reduced system and denote by .
Once all and are found, all can be recovered with perfect parallelism via
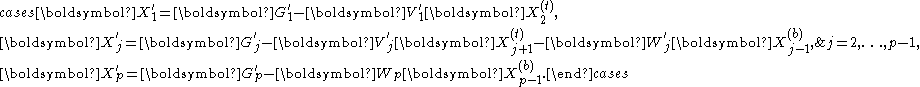
SPIKE as a polyalgorithmic banded linear system solver
Despite being logically divided into two stages, computationally, the SPIKE algorithm comprises three stages:- factorizingMatrix decompositionIn the mathematical discipline of linear algebra, a matrix decomposition is a factorization of a matrix into some canonical form. There are many different matrix decompositions; each finds use among a particular class of problems.- Example :...
the diagonal blocks, - computing the spikes,
- solving the reduced system.
Each of these stages can be accomplished in several ways, allowing a multitude of variants. Two notable variants are the recursive SPIKE algorithm for non-diagonally-dominantDiagonally dominant matrixIn mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other entries in that row...
cases and the truncated SPIKE algorithm for diagonally-dominant cases. Depending on the variant, a system can be solved either exactly or approximately. In the latter case, SPIKE is used as a preconditioner for iterative schemes like Krylov subspace methodIterative methodIn computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
s and iterative refinementIterative refinementIterative refinement is an iterative method proposed by James H. Wilkinson to improve the accuracy of numerical solutions to systems of linear equations....
.
Preprocessing stage
The first step of the preprocessing stage is to factorize the diagonal blocks . For numerical stability, one can use LAPACKLAPACK-External links:* : a modern replacement for PLAPACK and ScaLAPACK* on Netlib.org* * * : a modern replacement for LAPACK that is MultiGPU ready* on Sourceforge.net* * optimized LAPACK for Solaris OS on SPARC/x86/x64 and Linux* * *...
'sXGBTRFroutines to LU factorizeLU decompositionIn linear algebra, LU decomposition is a matrix decomposition which writes a matrix as the product of a lower triangular matrix and an upper triangular matrix. The product sometimes includes a permutation matrix as well. This decomposition is used in numerical analysis to solve systems of linear...
them with partial pivoting. Alternatively, one can also factorize them without partial pivoting but with a "diagonal boosting" strategy. The latter method tackles the issue of singular diagonal blocks.
In concrete terms, the diagonal boosting strategy is as follows. Let denote a configurable "machine zero". In each step of LU factorization, we require that the pivot satisfy the condition
- .
If the pivot does not satisfy the condition, it is then boosted by
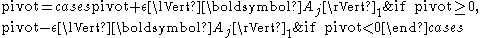
where is a positive parameter depending on the machine's unit roundoffMachine epsilonMachine epsilon gives an upper bound on the relative error due to rounding in floating point arithmetic. This value characterizes computer arithmetic in the field of numerical analysis, and by extension in the subject of computational science...
, and the factorization continues with the boosted pivot. This can be achieved by modified versions of ScaLAPACKScaLAPACKThe ScaLAPACK library includes a subset of LAPACK routines redesigned for distributed memory MIMD parallel computers. It is currently written in a Single-Program-Multiple-Data style using explicit message passing for interprocessor communication...
'sXDBTRFroutines. After the diagonal blocks are factorized, the spikes are computed and passed on to the postprocessing stage.
The two-partition case
In the two-partition case, i.e., when , the reduced system has the form
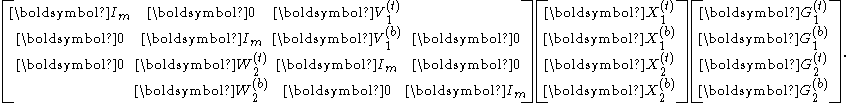
An even smaller system can be extracted from the center:
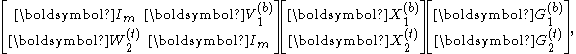
which can be solved using the block LU factorizationBlock LU decompositionIn linear algebra, a Block LU decomposition is a matrix decomposition of a block matrix into a lower block triangular matrix L and an upper block triangular matrix U...
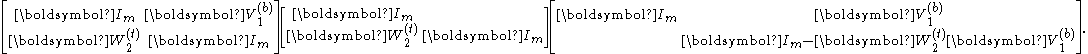
Once and are found, and can be computed via
- ,
- .
The multiple-partition case
Assume that is a power of two, i.e., . Consider a block diagonal matrix
where
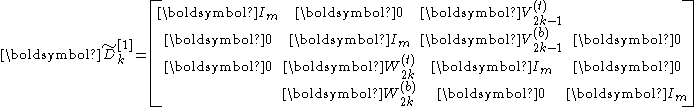
for . Notice that essentially consists of diagonal blocks of order extracted from . Now we factorize as
- .
The new matrix has the form
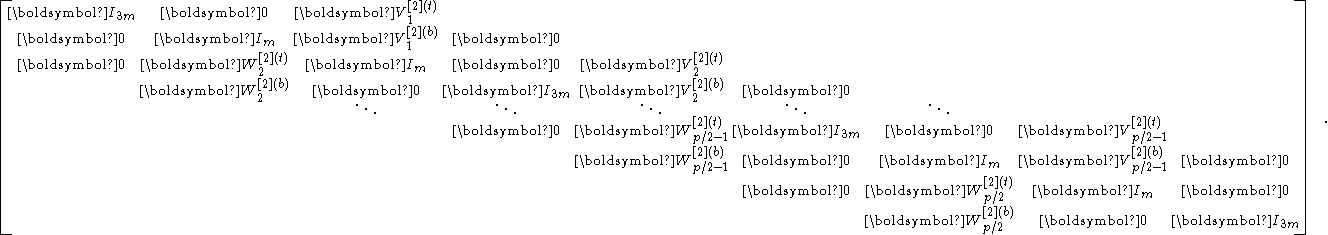
Its structure is very similar to that of , only differing in the number of spikes and their height (their width stays the same at ). Thus, a similar factorization step can be performed on to produce
and
- .
Such factorization steps can be performed recursively. After steps, we obtain the factorization
- ,
where has only two spikes. The reduced system will then be solved via
- .
The block LU factorization technique in the two-partition case can be used to handle the solving steps involving , …, and for they essentially solve multiple independent systems of generalized two-partition forms.
Generalization to cases where is not a power of two is almost trivial.
Truncated SPIKE
When is diagonally-dominant, in the reduced system
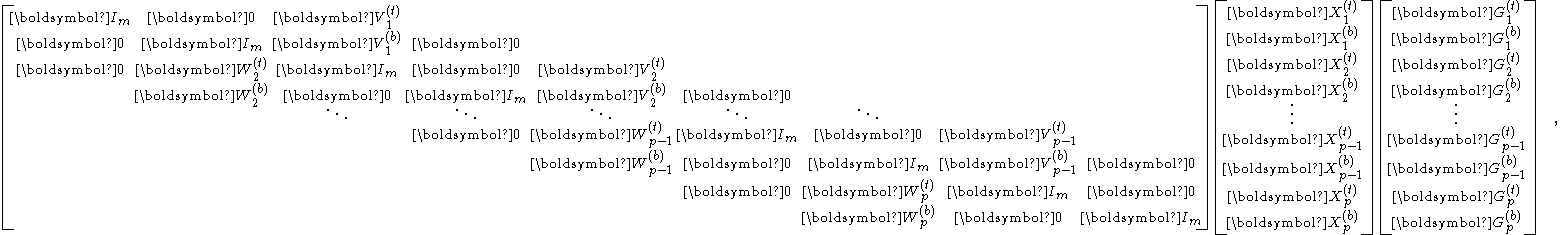
the blocks and are often negligible. With them omitted, the reduced system becomes block diagonal
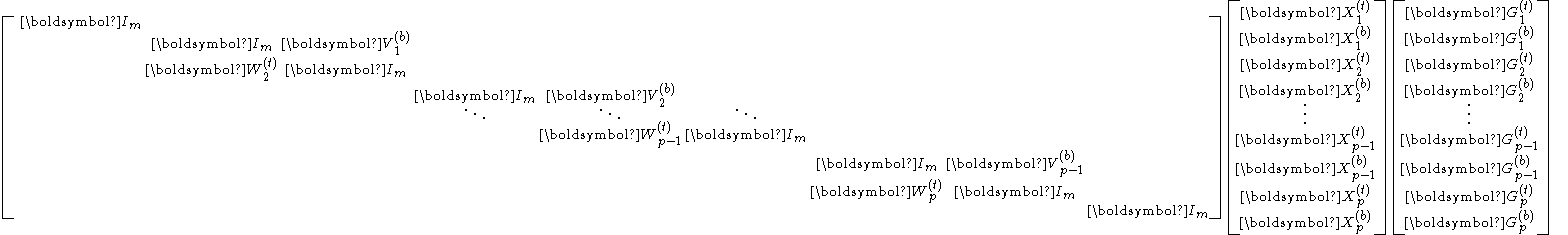
and can be easily solved in parallel.
The truncated SPIKE algorithm can be wrapped inside some outer iterative scheme (e.g., BiCGSTABBiconjugate gradient stabilized methodIn numerical linear algebra, the biconjugate gradient stabilized method, often abbreviated as BiCGSTAB, is an iterative method developed by H. A. van der Vorst for the numerical solution of nonsymmetric linear systems...
or iterative refinementIterative refinementIterative refinement is an iterative method proposed by James H. Wilkinson to improve the accuracy of numerical solutions to systems of linear equations....
) to improve the accuracy of the solution.
SPIKE as a preconditioner
The SPIKE algorithm can also function as a preconditioner for iterative methods for solving linear systems. To solve a linear system using a SPIKE-preconditioned iterative solver, one extracts center bands from to form a banded preconditioner and solves linear systems involving in each iteration with the SPIKE algorithm.
In order for the preconditioner to be effective, row and/or column permutation is usually necessary to move “heavy” elements of close to the diagonal so that they are covered by the preconditioner. This can be accomplished by computing the weighted spectral reordering of .
The SPIKE algorithm can be generalized by not restricting the preconditioner to be strictly banded. In particular, the diagonal block in each partition can be a general matrix and thus handled by a direct general linear system solver rather than a banded solver. This enhances the preconditioner, and hence allows better chance of convergence and reduces the number of iterations.
Implementations
Intel offers an implementation of the SPIKE algorithm under the name Intel Adaptive Spike-Based Solver.- factorizing

