STAR model - AbsoluteAstronomy.com

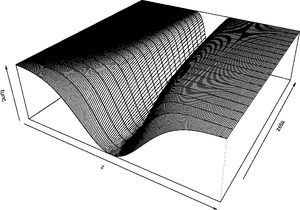
Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, Smooth Transition Autoregressive (STAR) models are typically applied to time series

Time series

In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...

data as an extension of autoregressive models, in order to allow for higher degree of flexibility in model parameters through a smooth transition.

Given a time series of data x_t, the STAR model is a tool for understanding and, perhaps, predicting future values in this series, assuming that the behaviour of the series changes depending on the value of the transition variable. The transition might depend on the past values of the x series (similar to the SETAR models), or exogenous variables.

The model consists of 2 autoregressive (AR) parts linked by the transition function. The model is usually referred to as the STAR(p) models proceeded by the letter describing the transition function (see below) and p is the order of the autoregressive part. Most popular transition function include exponential function and first and second-order logistic functions. They give rise to Logistic STAR (LSTAR) and Exponential STAR (ESTAR) models.

Autoregressive Models

Consider a simple AR(p}) model for a time series

Time series

y_t

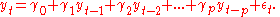
where:

for i=1,2,...,p are autoregressive coefficients, assumed to be constant over time;

stands for white-noise error term with constant variance

Variance

In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...

.
written in a following vector form:

where:

is a column vector of variables;

is the vector of parameters :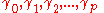

;

stands for white-noise error term with constant variance

Variance

STAR as an Extension of the Autoregressive Model

STAR models were introduced and comprehensively developed by Kung-sik Chan and Howell Tong in 1986, in which the same acronym was used. It originally stands for Smooth Threshold Autoregressive. The models can be thought of in terms of extension of autoregressive models, allowing for changes in the model parameters according to the value of weakly exogenous

Exogenous

Exogenous refers to an action or object coming from outside a system. It is the opposite of endogenous, something generated from within the system....

transition variable z_t.

Defined in this way, STAR model can be presented as follows:

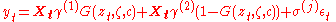
where:

is a column vector of variables;

is the transition function bounded between 0 and 1.

Basic Structure

They can be understood as two-regime SETAR model with smooth transition between regimes, or as continuum of regimes. In both cases the presence of the transition function is the defining feature of the model as it allows for changes in values of the parameters.

Transition Function

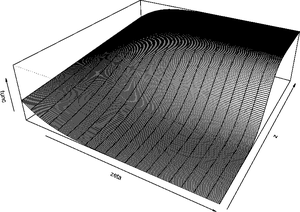
Three basic transition functions and the name of resulting models are:

first order logistic function - results in Logistic STAR (LSTAR) model:
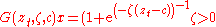
exponential function - results in Exponential STAR (ESTAR) model:
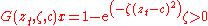
second order logistic function:

Autoregressive Models

STAR as an Extension of the Autoregressive Model

Basic Structure

Transition Function

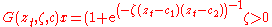
See also