In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a semi-local ring is a ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 for which R/J(R) is a semisimple ring, where J(R) is the Jacobson radical

Jacobson radical

In mathematics, more specifically ring theory, a branch of abstract algebra, the Jacobson radical of a ring R is an ideal which consists of those elements in R which annihilate all simple right R-modules. It happens that substituting "left" in place of "right" in the definition yields the same...

 of R.

The above definition implies R has a finite number of maximal right ideals (and finite number of maximal left ideals). When R is a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

, the converse implication is also true, and so the definition of semi-local for commutative rings is often taken to be "having finitely many maximal ideal

Maximal ideal

In mathematics, more specifically in ring theory, a maximal ideal is an ideal which is maximal amongst all proper ideals. In other words, I is a maximal ideal of a ring R if I is an ideal of R, I ≠ R, and whenever J is another ideal containing I as a subset, then either J = I or J = R...

s".

Some literature refers to a commutative semi-local ring in general as a
quasi-semi-local ring, using semi-local ring to refer to a Noetherian ring

Noetherian ring

In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...

 with finitely many maximal ideals.

A semi-local ring is thus more general than a local ring

Local ring

In abstract algebra, more particularly in ring theory, local rings are certain rings that are comparatively simple, and serve to describe what is called "local behaviour", in the sense of functions defined on varieties or manifolds, or of algebraic number fields examined at a particular place, or...

, which has only one maximal (right/left/two-sided) ideal.

Examples

• Any right or left Artinian ring
  Artinian ring
  In abstract algebra, an Artinian ring is a ring that satisfies the descending chain condition on ideals. They are also called Artin rings and are named after Emil Artin, who first discovered that the descending chain condition for ideals simultaneously generalizes finite rings and rings that are...
  
  , any serial ring, and any semiperfect ring
  Semiperfect ring
  In abstract algebra, a semiperfect ring is a ring over which every finitely generated left module has a projective cover. This property is left right symmetric.- Definition :Let R be ring...
  
   is semi-local.
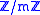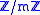• The quotient is a semi-local ring. In particular, if is a prime power, then is a local ring.
• A finite direct sum of fields is a semi-local ring.
• In the case of commutative rings with unity, this example is prototypical in the following sense: the Chinese remainder theorem
  Chinese remainder theorem
  The Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
  
   shows that for a semi-local commutative ring R with unit and maximal ideals m₁, ..., m_n.. The right hand side is a direct sum of fields. Here we note that ∩_i m_i=J(R), and we see that R/J(R) is indeed a semisimple ring.
• The classical ring of quotients for any commutative Noetherian ring is a semilocal ring.
• The endomorphism ring
  Endomorphism ring
  In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
  
   of an Artinian module
  Artinian module
  In abstract algebra, an Artinian module is a module that satisfies the descending chain condition on its poset of submodules. They are for modules what Artinian rings are for rings, and a ring is Artinian if and only if it is an Artinian module over itself...
  
   is a semilocal ring.
• Semi-local rings occur for example in algebraic geometry
  Algebraic geometry
  Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
  
   when a (commutative) ring R is localized
  Localization of a ring
  In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
  
   with respect to the multiplicatively closed subset S = ∩ (R \ p_i), where the p_i are finitely many prime ideal
  Prime ideal
  In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
  
  s.