
Shriek map
Encyclopedia
In category theory
, a branch of mathematics
, certain unusual functor
s are denoted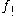 and
and 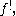 with the exclamation mark
with the exclamation mark
used to indicate that they are exceptional in some way. They are thus accordingly sometimes called shriek maps, with "shriek
" being slang for an exclamation mark, though other terms are used, depending on context.
, these arise in image functors for sheaves
, particularly
Verdier duality
, where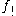 is a "less usual" functor.
is a "less usual" functor.
In algebraic topology
, these arise particularly in fiber bundle
s, where they yield maps that have the opposite of the usual variance. They are thus called wrong way maps, Gysin maps, as they originated in the Gysin sequence
, or transfer maps. A fiber bundle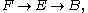 with base space B, fiber F, and total space E, has, like any other continuous map of topological spaces, a covariant map on homology
with base space B, fiber F, and total space E, has, like any other continuous map of topological spaces, a covariant map on homology 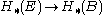 and a contravariant map on cohomology
and a contravariant map on cohomology  However, it also has a covariant map on cohomology, corresponding in de Rham cohomology
However, it also has a covariant map on cohomology, corresponding in de Rham cohomology
to "integration along the fiber", and a contravariant map on homology, corresponding in de Rham cohomology to "pointwise product with the fiber". The composition of the "wrong way" map with the usual map gives a map from the homology of the base to itself, analogous to a unit/counit of an adjunction; compare also Galois connection
.
These can be used in understanding and proving the product property for the Euler characteristic of a fiber bundle.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, certain unusual functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s are denoted
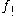 and
and 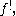 with the exclamation mark
with the exclamation markExclamation mark
The exclamation mark, exclamation point, or bang, or "dembanger" is a punctuation mark usually used after an interjection or exclamation to indicate strong feelings or high volume , and often marks the end of a sentence. Example: “Watch out!” The character is encoded in Unicode at...
used to indicate that they are exceptional in some way. They are thus accordingly sometimes called shriek maps, with "shriek
Shriek
Shriek may refer to:* A kind of vociferation* a slang term for the exclamation mark, used in some computing and mathematical contexts, such as f_! and f^! being called shriek maps....
" being slang for an exclamation mark, though other terms are used, depending on context.
Usage
Shriek notation is used in two senses:- To distinguish a functor from a more usual functor
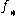 or
or 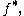 accordingly as it is covariant or contravariant.
accordingly as it is covariant or contravariant. - To indicate a map that goes "the wrong way" – a functor that has the same objects as a more familiar functor, but behaves differently on maps and has the opposite variance. For example, it has a pull-back where one expects a push-forward.
Examples
In algebraic geometryAlgebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, these arise in image functors for sheaves
Image functors for sheaves
In mathematics, especially in sheaf theory, a domain applied in areas such as topology, logic and algebraic geometry, there are four image functors for sheaves which belong together in various senses....
, particularly
Verdier duality
Verdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
, where
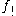 is a "less usual" functor.
is a "less usual" functor.In algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, these arise particularly in fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s, where they yield maps that have the opposite of the usual variance. They are thus called wrong way maps, Gysin maps, as they originated in the Gysin sequence
Gysin sequence
In the field of mathematics known as algebraic topology, the Gysin sequence is a long exact sequence which relates the cohomology classes of the base space, the fiber and the total space of a sphere bundle. The Gysin sequence is a useful tool for calculating the cohomology rings given the Euler...
, or transfer maps. A fiber bundle
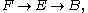 with base space B, fiber F, and total space E, has, like any other continuous map of topological spaces, a covariant map on homology
with base space B, fiber F, and total space E, has, like any other continuous map of topological spaces, a covariant map on homology 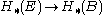 and a contravariant map on cohomology
and a contravariant map on cohomology  However, it also has a covariant map on cohomology, corresponding in de Rham cohomology
However, it also has a covariant map on cohomology, corresponding in de Rham cohomologyDe Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
to "integration along the fiber", and a contravariant map on homology, corresponding in de Rham cohomology to "pointwise product with the fiber". The composition of the "wrong way" map with the usual map gives a map from the homology of the base to itself, analogous to a unit/counit of an adjunction; compare also Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
.
These can be used in understanding and proving the product property for the Euler characteristic of a fiber bundle.

