Image functors for sheaves
Encyclopedia
In mathematics
, especially in sheaf theory
, a domain applied in areas such as topology
, logic
and algebraic geometry
, there are four image functors for sheaves which belong together in various senses.
Given a continuous mapping f: X → Y of topological space
s, and the category
Sh(–) of sheaves of abelian group
s on a topological space. The functors in question are
The exclamation mark
is often pronounced "shriek
" (slang for exclamation mark), and the maps called "f shriek" or "f lower shriek" and "f upper shriek" – see also shriek map
.
The exceptional inverse image is in general defined on the level of derived categories
only. Similar considerations apply to étale sheaves
on schemes
.
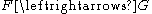means that F is left adjoint to G (equivalently G right adjoint to F), i.e.
for any two objects A, B in the two categories being adjoint by F and G.
For example, f∗ is the left adjoint of f*. By the standard reasoning with adjointness relations, there are natural unit and counit morphisms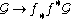
and 
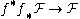for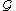 
on Y and 
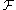on X, respectively. However, these are almost never isomorphisms - see the localization example below.
gives another link between them: morally speaking, it exchanges "∗" and "!", i.e. in the synopsis above it exchanges functors along the diagonals. For example the direct image is dual to the direct image with compact support. This phenomenon is studied and used in the theory of perverse sheaves
.
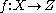and 
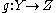, which induce morphisms 
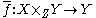and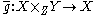 
.
Then there exists a canonical isomorphism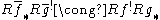
.
open subset j: U ⊂ X, the situation simplifies insofar that for j∗=j! and i!=i∗ and for any sheaf F on X, one gets exact sequence
s
Its Verdier dual reads
a distinguished triangle in the derived category of sheaves on X.
The adjointness relations read in this case
and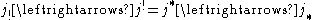
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in sheaf theory
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
, a domain applied in areas such as topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, logic
Logic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, there are four image functors for sheaves which belong together in various senses.
Given a continuous mapping f: X → Y of topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
s, and the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
Sh(–) of sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s on a topological space. The functors in question are
- direct imageDirect image functorIn mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.-Definition:...
f∗ : Sh(X) → Sh(Y) - inverse imageInverse image functorIn mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
f∗ : Sh(Y) → Sh(X) - direct image with compact supportDirect image with compact supportIn mathematics, in the theory of sheaves the direct image with compact support is an image functor for sheaves.-Definition:Let f: X → Y be a continuous mapping of topological spaces, and Sh the category of sheaves of abelian groups on a topological space...
f! : Sh(X) → Sh(Y) - exceptional inverse imageExceptional inverse image functorIn mathematics, more specifically sheaf theory, a branch of topology and algebraic geometry, the exceptional inverse image functor is the fourth and most sophisticated in a series of image functors for sheaves. It is needed to express Verdier duality in its most general form.-Definition:Let f: X →...
Rf! : D(Sh(Y)) → D(Sh(X)).
The exclamation mark
Exclamation mark
The exclamation mark, exclamation point, or bang, or "dembanger" is a punctuation mark usually used after an interjection or exclamation to indicate strong feelings or high volume , and often marks the end of a sentence. Example: “Watch out!” The character is encoded in Unicode at...
is often pronounced "shriek
Shriek
Shriek may refer to:* A kind of vociferation* a slang term for the exclamation mark, used in some computing and mathematical contexts, such as f_! and f^! being called shriek maps....
" (slang for exclamation mark), and the maps called "f shriek" or "f lower shriek" and "f upper shriek" – see also shriek map
Shriek map
In category theory, a branch of mathematics, certain unusual functors are denoted f_! and f^!, with the exclamation mark used to indicate that they are exceptional in some way...
.
The exceptional inverse image is in general defined on the level of derived categories
Derived category
In mathematics, the derived category D of an abelian category C is a construction of homological algebra introduced to refine and in a certain sense to simplify the theory of derived functors defined on C...
only. Similar considerations apply to étale sheaves
Étale
In mathematics, more specifically in algebra, the adjective étale refers to several closely related concepts:* Étale morphism** Formally étale morphism* Étale cohomology* Étale topology* Étale fundamental group* Étale space* Étale group scheme...
on schemes
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
.
Adjointness
The functors are adjoint to each other as depicted at the right, where, as usual,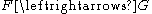 means that F is left adjoint to G (equivalently G right adjoint to F), i.e.
- HomMorphismIn mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
(F(A), B) ≅ Hom(A, G(B))
for any two objects A, B in the two categories being adjoint by F and G.
For example, f∗ is the left adjoint of f*. By the standard reasoning with adjointness relations, there are natural unit and counit morphisms
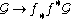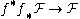and for 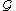on Y and 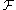on X, respectively. However, these are almost never isomorphisms - see the localization example below.Verdier duality
Verdier dualityVerdier duality
In mathematics, Verdier duality is a generalization of the Poincaré duality of manifolds to locally compact spaces with singularities. Verdier duality was introduced by , as an analog for locally compact spaces of the coherent duality for schemes due to Grothendieck...
gives another link between them: morally speaking, it exchanges "∗" and "!", i.e. in the synopsis above it exchanges functors along the diagonals. For example the direct image is dual to the direct image with compact support. This phenomenon is studied and used in the theory of perverse sheaves
Perverse sheaf
The mathematical term perverse sheaves refers to a certain abelian category associated to a topological space X, which may be a real or complex manifold, or a more general Topologically stratified space, usually singular...
.
Base Change
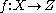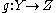Another useful property of the image functors is base change. Given continuous maps and , which induce morphisms 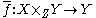and 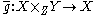.Then there exists a canonical isomorphism
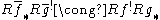.Localization
In the particular situation of a closed subspace i: Z ⊂ X and the complementaryComplement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
open subset j: U ⊂ X, the situation simplifies insofar that for j∗=j! and i!=i∗ and for any sheaf F on X, one gets exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s
- 0 → j!j∗ F → F → i∗i∗ F → 0
Its Verdier dual reads
- i∗Ri! F → F → Rj∗j∗ F → i∗Ri! F[1],
a distinguished triangle in the derived category of sheaves on X.
The adjointness relations read in this case
and
.
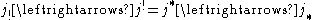