Siegel disc
Encyclopedia
Siegel disc is a connected component in the Fatou set
where the dynamics is analytically conjugated
to an irrational rotation.
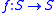on a Riemann surface
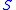we consider the dynamical system
generated by the iterates
of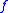
denoted by 
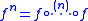. We then call the orbit
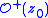of 
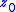as the set of forward iterates of 
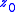. We are interested in the asymptotic behavior of the orbits in 
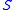(which will usually be 
, the complex plane
or
, the Riemann sphere
), and we call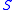
the phase plane
or dynamical plane.
One possible asymptotic behavior for a point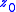
is to be a fixed point
, or in general a periodic point. In this last case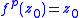
where 
is the period
and
means 
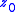is a fixed point. We can then define the multiplier of the orbit as 
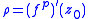and this enables us to classify periodic orbits as attracting if 
superattracting if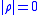 
), repelling if 
and indifferent if 
. Indifferent periodic orbits split in rationally indifferent and irrationally indifferent, depending on whether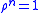 
for some 
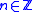or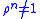 
for all 
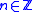, respectively.
Siegel discs are one of the possible cases of connected components in the Fatou set (the complementary set of the Julia set
), according to Classification of Fatou components
, and can occur around irrationally indifferent periodic points. The Fatou set is, roughly, the set of points where the iterates behave similarly to their neighbours (they form a normal family
). Siegel discs correspond to points where the dynamics of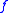
is analytically
conjugated
to an irrational rotation of the complex disc.
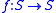be a holomorphic endomorphism
where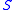
is a Riemann surface
, and let U be a connected component of the Fatou set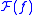
. We say U is a Siegel disc of f around the point z_0 if there exists an analytic homeomorphism 
where 
is the unit disc and such that 
for some 
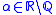and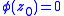 
.
Siegel's
theorem proves the existence of Siegel discs for irrational numbers
satisfying a strong irrationality condition (a Diophantine condition), thus solving an open problem since Fatou conjectured his theorem on the Classification of Fatou components
.
Later A. D. Brjuno improved this condition on the irrationality, enlarging it to the Brjuno numbers.
This is part of the result from the Classification of Fatou components
.
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
where the dynamics is analytically conjugated
Topological conjugation
In mathematics, two functions are said to be topologically conjugate to one another if there exists a homeomorphism that will conjugate the one into the other...
to an irrational rotation.
Description
Given a holomorphic endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
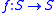on a Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
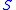we consider the dynamical systemDynamical system
A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...
generated by the iterates
Iterated function
In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...
of
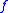denoted by 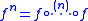. We then call the orbitOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
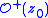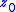of as the set of forward iterates of 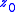. We are interested in the asymptotic behavior of the orbits in 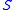(which will usually be , the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
or
, the Riemann sphereRiemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
), and we call
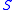the phase planePhase plane
A phase plane is a visual display of certain characteristics of certain kinds of differential equations; it is a 2-dimensional version of the general n-dimensional phase space....
or dynamical plane.
One possible asymptotic behavior for a point
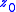is to be a fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
, or in general a periodic point. In this last case
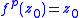where is the periodOrbit (dynamics)
In mathematics, in the study of dynamical systems, an orbit is a collection of points related by the evolution function of the dynamical system. The orbit is a subset of the phase space and the set of all orbits is a partition of the phase space, that is different orbits do not intersect in the...
and
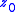means is a fixed point. We can then define the multiplier of the orbit as 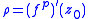and this enables us to classify periodic orbits as attracting if superattracting if 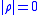), repelling if and indifferent if . Indifferent periodic orbits split in rationally indifferent and irrationally indifferent, depending on whether 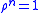for some 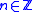or 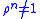for all 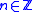, respectively.Siegel discs are one of the possible cases of connected components in the Fatou set (the complementary set of the Julia set
Julia set
In the context of complex dynamics, a topic of mathematics, the Julia set and the Fatou set are two complementary sets defined from a function...
), according to Classification of Fatou components
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
, and can occur around irrationally indifferent periodic points. The Fatou set is, roughly, the set of points where the iterates behave similarly to their neighbours (they form a normal family
Normal family
In mathematics, with special application to complex analysis, a normal family is a pre-compact family of continuous functions. Informally, this means that the functions in the family are not exceedingly numerous or widely spread out; rather, they stick together in a relatively "compact" manner...
). Siegel discs correspond to points where the dynamics of
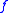is analyticallyconjugated
Topological conjugation
In mathematics, two functions are said to be topologically conjugate to one another if there exists a homeomorphism that will conjugate the one into the other...
to an irrational rotation of the complex disc.
Formal definition
Let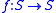 be a holomorphic endomorphismEndomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
where
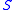is a Riemann surfaceRiemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
, and let U be a connected component of the Fatou set
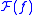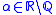. We say U is a Siegel disc of f around the point z_0 if there exists an analytic homeomorphism where is the unit disc and such that for some and 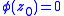.Siegel's
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
theorem proves the existence of Siegel discs for irrational numbers
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
satisfying a strong irrationality condition (a Diophantine condition), thus solving an open problem since Fatou conjectured his theorem on the Classification of Fatou components
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
.
Later A. D. Brjuno improved this condition on the irrationality, enlarging it to the Brjuno numbers.
This is part of the result from the Classification of Fatou components
Classification of Fatou components
In mathematics, if f = P/Q is a rational function defined in the extended complex plane, and ifthen for a periodic component U of the Fatou set, exactly one of the following holds:# U contains an attracting periodic point# U is parabolic...
.