Sigma is the eighteenth letter of the Greek alphabet

Greek alphabet

The Greek alphabet is the script that has been used to write the Greek language since at least 730 BC . The alphabet in its classical and modern form consists of 24 letters ordered in sequence from alpha to omega...

, and carries the 'S' sound. In the system of Greek numerals

Greek numerals

Greek numerals are a system of representing numbers using letters of the Greek alphabet. They are also known by the names Ionian numerals, Milesian numerals , Alexandrian numerals, or alphabetic numerals...

 it has a value of 200. When used at the end of a word, and the word is not all upper case, the final form (ς) is used, e.g. (Odysseus) – note the two sigmas in the center of the name, and the word-final sigma at the end.

History

The shape and alphabetic position of Sigma is derived from Phoenician

Phoenician alphabet

The Phoenician alphabet, called by convention the Proto-Canaanite alphabet for inscriptions older than around 1050 BC, was a non-pictographic consonantal alphabet, or abjad. It was used for the writing of Phoenician, a Northern Semitic language, used by the civilization of Phoenicia...

 shin

Shin (letter)

Shin literally means "Sharp" ; It is the twenty-first letter in many Semitic abjads, including Phoenician , Aramaic/Hebrew , and Arabic ....

 , but the sound is derived from Phoenician samekh

Samekh

Samekh or Simketh is the fifteenth letter in many Semitic alphabets, including Phoenician, Hebrew, and Aramaic, representing . The Arabic alphabet, however, uses a letter based on Phoenician šin to represent ; however, that glyph takes Samekh's place in the traditional Abjadi order of the Arabic...

, which appear as inconsistency in transcribing sibilants.

Etymology

The name of sigma, according to one theory, may continue that of Phoenician Samekh

Samekh

Samekh or Simketh is the fifteenth letter in many Semitic alphabets, including Phoenician, Hebrew, and Aramaic, representing . The Arabic alphabet, however, uses a letter based on Phoenician šin to represent ; however, that glyph takes Samekh's place in the traditional Abjadi order of the Arabic...

. According to a different theory, its original name may have been "San

San (letter)

San was an archaic letter of the Greek alphabet. Its shape was similar to modern M, or to a modern Greek Sigma turned sideways, and it was used as an alternative to Sigma to denote the sound . Unlike Sigma, whose position in the alphabet is between Rho and Tau, San appeared between Pi and Qoppa...

" (the name today associated with another, obsolete letter), while "Sigma" was a Greek innovation that simply meant "hissing", based on a nominalization of a verb (sízō, from earlier *sig-jō, meaning 'I hiss').

Uppercase of esh

The uppercase form of sigma was re-borrowed into the Latin alphabet

Latin alphabet

The Latin alphabet, also called the Roman alphabet, is the most recognized alphabet used in the world today. It evolved from a western variety of the Greek alphabet called the Cumaean alphabet, which was adopted and modified by the Etruscans who ruled early Rome...

 to serve as the uppercase of modern esh

Esh (letter)

Esh is a character used in conjunction with the Latin Alphabet. Its lowercase form is similar to an italic long s ſ or an integral sign ∫; in 1928 the Africa Alphabet borrowed the Greek letter sigma for the uppercase form , but more recently the African reference alphabet discontinued it, using...

 (lowercase: ).

Lunate sigma

In handwritten Greek during the Hellenistic period (4th and 3rd centuries BC), the epigraphic form of Σ was simplified into a C-like shape. It is also found on coins from the fourth century BC onwards. This became the universal standard form of Sigma during late antiquity and the Middle Ages. It is today known as lunate sigma (upper case , lower case ), because of its crescent

Crescent

In art and symbolism, a crescent is generally the shape produced when a circular disk has a segment of another circle removed from its edge, so that what remains is a shape enclosed by two circular arcs of different diameters which intersect at two points .In astronomy, a crescent...

-like shape.

It is still widely used in decorative typefaces in Greece, especially in religious and church contexts, as well as in some modern print editions of classical Greek texts. The forms of the Cyrillic letter

Cyrillic alphabet

The Cyrillic script or azbuka is an alphabetic writing system developed in the First Bulgarian Empire during the 10th century AD at the Preslav Literary School...

 С

Es (Cyrillic)

Es is a letter of the Cyrillic alphabet.It commonly represents the voiceless alveolar fricative , like the pronunciation of ⟨s⟩ in "sand".-History:...

 (representing /s/) and Coptic letter

Coptic alphabet

The Coptic alphabet is the script used for writing the Coptic language. The repertoire of glyphs is based on the Greek alphabet augmented by letters borrowed from the Demotic and is the first alphabetic script used for the Egyptian language...

  sima are derived from lunate sigma.

A dotted lunate sigma (sigma periestigmenon, encoded at U+03FE ) was used by Aristarchus of Samothrace

Aristarchus of Samothrace

Aristarchus of Samothrace was a grammarian noted as the most influential of all scholars of Homeric poetry. He was the librarian of the library of Alexandria and seems to have succeeded his teacher Aristophanes of Byzantium in that role.He established the most historically important critical...

 as an editorial sign indicating that the line so marked is at an incorrect position. Similarly, an antisigma or reversed sigma may mark a line that is out of place. A dotted antisigma or dotted reversed sigma (antisigma periestigmenon: ) may indicate a line after which rearrangements should be made, or to variant readings of uncertain priority.

Greek

In both Ancient

Ancient Greek

Ancient Greek is the stage of the Greek language in the periods spanning the times c. 9th–6th centuries BC, , c. 5th–4th centuries BC , and the c. 3rd century BC – 6th century AD of ancient Greece and the ancient world; being predated in the 2nd millennium BC by Mycenaean Greek...

 and Modern Greek

Modern Greek

Modern Greek refers to the varieties of the Greek language spoken in the modern era. The beginning of the "modern" period of the language is often symbolically assigned to the fall of the Byzantine Empire in 1453, even though that date marks no clear linguistic boundary and many characteristic...

, the sigma represents the voiceless alveolar fricative

Voiceless alveolar fricative

The voiceless alveolar sibilant is a common consonant sound in spoken languages. It is the sound in English words such as sea and pass, and is represented in the International Phonetic Alphabet as . It has a characteristic high-pitched, highly perceptible hissing sound...

 /s/. Both in Ancient and Modern Greek, this sound is voiced

Voice (phonetics)

Voice or voicing is a term used in phonetics and phonology to characterize speech sounds, with sounds described as either voiceless or voiced. The term, however, is used to refer to two separate concepts. Voicing can refer to the articulatory process in which the vocal cords vibrate...

 to /z/ before /m/ or /n/.

Berber

Upper case Σ may be used in the Berber Latin alphabet

Berber Latin alphabet

The Berber Latin alphabet is the version of the Latin alphabet used to write the Berber language...

 for [ʕ], though the INALCO standard uses Ɛ instead.

Upper case

Upper case Σ is used as a symbol for:

• the summation
  Summation
  Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
  
   operator
• a class of baryon
  Baryon
  A baryon is a composite particle made up of three quarks . Baryons and mesons belong to the hadron family, which are the quark-based particles...
  
  s in particle physics
  Particle physics
  Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
  
  
• macroscopic cross section
  Cross section (physics)
  A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
  
  s in nuclear
  Nuclear physics
  Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...
  
   and particle physics
• self-energy
  Self-energy
  In theoretical physics and quantum field theory a particle's self-energy \Sigma represents the contribution to the particle's energy, or effective mass, due to interactions between the particle and the system it is part of...
  
   in condensed matter physics
  Condensed matter physics
  Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
  
  
• the balance
  Balance (accounting)
  In banking and accountancy, the outstanding balance is the amount of money owed, , that remains in a deposit account at a given date, after all past remittances, payments and withdrawal have been accounted for. It can be positive or negative ....
  
   of the invoice classes and the overall amount of the debts and demands in economics
  Economics
  Economics is the social science that analyzes the production, distribution, and consumption of goods and services. The term economics comes from the Ancient Greek from + , hence "rules of the house"...
  
  
• the set of symbols that form an alphabet in linguistics
  Linguistics
  Linguistics is the scientific study of human language. Linguistics can be broadly broken into three categories or subfields of study: language form, language meaning, and language in context....
  
   and computer science
  Computer science
  Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
  
  
• the covariance matrix
  Covariance matrix
  In probability theory and statistics, a covariance matrix is a matrix whose element in the i, j position is the covariance between the i th and j th elements of a random vector...
  
   of a set of random variables in probability theory
  Probability theory
  Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
  
   and statistics
  Statistics
  Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
  
  

Lower case

Lower case σ is used for:

• sigma bond
  Sigma bond
  In chemistry, sigma bonds are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most clearly defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is...
  
  s in chemistry
  Chemistry
  Chemistry is the science of matter, especially its chemical reactions, but also its composition, structure and properties. Chemistry is concerned with atoms and their interactions with other atoms, and particularly with the properties of chemical bonds....
  
  
• Sigma constant in science
• the sigma receptor
  Sigma receptor
  The sigma receptors σ1 and σ2 bind to ligands such as 4-PPBP, SA 4503, ditolylguanidine, dimethyltryptamine and siramesine.- Classification :...
  
   in biology
  Biology
  Biology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
  
  
• the standard deviation
  Standard deviation
  Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
  
   of a population or probability distribution
  Probability distribution
  In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
  
   in statistics
  Statistics
  Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
  
  
• a quality model for business, Six Sigma
  Six Sigma
  Six Sigma is a business management strategy originally developed by Motorola, USA in 1986. , it is widely used in many sectors of industry.Six Sigma seeks to improve the quality of process outputs by identifying and removing the causes of defects and minimizing variability in manufacturing and...
  
  , based on the standard deviation
  Standard deviation
  Standard deviation is a widely used measure of variability or diversity used in statistics and probability theory. It shows how much variation or "dispersion" there is from the average...
  
  , often referred to as "6σ"
• sigma-algebra
  Sigma-algebra
  In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
  
  s, sigma-fields and sigma-finiteness
  Sigma-finite measure
  In mathematics, a positive measure μ defined on a σ-algebra Σ of subsets of a set X is called finite if μ is a finite real number . The measure μ is called σ-finite if X is the countable union of measurable sets of finite measure...
  
   in measure theory
  Measure (mathematics)
  In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
  
  ; more generally, the symbol σ serves as a shorthand for "countably
  Countable set
  In mathematics, a countable set is a set with the same cardinality as some subset of the set of natural numbers. A set that is not countable is called uncountable. The term was originated by Georg Cantor...
  
  ", e.g. a σ-compact topological space
  Topological space
  Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
  
   is one that can be written as a countable union
  Union (set theory)
  In set theory, the union of a collection of sets is the set of all distinct elements in the collection. The union of a collection of sets S_1, S_2, S_3, \dots , S_n\,\! gives a set S_1 \cup S_2 \cup S_3 \cup \dots \cup S_n.- Definition :...
  
   of compact subsets
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  .
• the generated sigma-algebra of a set is denoted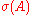
• the sum-of-divisors function
  Divisor function
  In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
  
   in number theory
  Number theory
  Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
  
  
• the Stefan–Boltzmann constant
• the "sigma factor
  Sigma factor
  A sigma factor is a bacterial transcription initiation factor that enables specific binding of RNA polymerase to gene promoters. Different sigma factors are activated in response to different environmental conditions...
  
  " of RNA polymerase
  RNA polymerase
  RNA polymerase is an enzyme that produces RNA. In cells, RNAP is needed for constructing RNA chains from DNA genes as templates, a process called transcription. RNA polymerase enzymes are essential to life and are found in all organisms and many viruses...
  
  
• a measure of electrical conductivity
• the Surface charge
  Surface charge
  Surface charge is the electric charge present at an interface. There are many different processes which can lead to a surface being charged, including adsorption of ions, protonation/deprotonation, and the application of an external electric field...
  
   density in electrostatics
• Normal stress
  Stress (physics)
  In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
  
   in continuum mechanics
  Continuum mechanics
  Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
  
  
• volatility of a stock
  Stock
  The capital stock of a business entity represents the original capital paid into or invested in the business by its founders. It serves as a security for the creditors of a business since it cannot be withdrawn to the detriment of the creditors...
  
   generally needed for options pricing
• a syllable
  Syllable
  A syllable is a unit of organization for a sequence of speech sounds. For example, the word water is composed of two syllables: wa and ter. A syllable is typically made up of a syllable nucleus with optional initial and final margins .Syllables are often considered the phonological "building...
  
   in phonology
  Phonology
  Phonology is, broadly speaking, the subdiscipline of linguistics concerned with the sounds of language. That is, it is the systematic use of sound to encode meaning in any spoken human language, or the field of linguistics studying this use...
  
  
• the spectrum of a matrix
  Spectrum of a matrix
  In mathematics, the spectrum of a matrix is the set of its eigenvalues. This notion can be extended to the spectrum of an operator in the infinite-dimensional case.The determinant equals the product of the eigenvalues...
  
   , denoted as 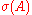, in applied mathematics
  Applied mathematics
  Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
  
  
• surface tension
  Surface tension
  Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
  
  
• the unary operation
  Unary operation
  In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
  
   of selection on a database relation in relational algebra
  Relational algebra
  Relational algebra, an offshoot of first-order logic , deals with a set of finitary relations that is closed under certain operators. These operators operate on one or more relations to yield a relation...
  
  
• the Pauli matrices
  Pauli matrices
  The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...
  
   in quantum mechanics
  Quantum mechanics
  Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
  
  
• a target's radar cross-section (RCS) in radar jamming or Electronic Warfare
  Electronic warfare
  Electronic warfare refers to any action involving the use of the electromagnetic spectrum or directed energy to control the spectrum, attack an enemy, or impede enemy assaults via the spectrum. The purpose of electronic warfare is to deny the opponent the advantage of, and ensure friendly...
  
   (EW)
• the life span of a basic multicellular unit (BMU) in bone remodeling
  Bone remodeling
  Bone remodeling is a lifelong process where mature bone tissue is removed from the skeleton and new bone tissue is formed...
  
  
• the Damping Parameter in Signal processing.

Politics

During the 1930s, an upper case Σ was in use as the symbol of the Ação Integralista Brasileira

Brazilian Integralism

Brazilian Integralism was a fascist political movement in Brazil, created on October 1932. Founded and led by Plínio Salgado, a literary figure who was somewhat famous for his participation in the 1922 Modern Art Week, the movement had adopted some characteristics of European mass movements of...

, a radical right-wing party in Brazil

Brazil

Brazil , officially the Federative Republic of Brazil , is the largest country in South America. It is the world's fifth largest country, both by geographical area and by population with over 192 million people...

.

Unicode

description	character	Unicode	HTML
Greek
SIGMA	Σ σ	U+03A3 U+03C3	Σ σ
SMALL LETTER FINAL SIGMA	ς	U+03C2	ς
LUNATE SIGMA SYMBOL	Ϲ ϲ	U+03F9 U+03F2	Ϲ ϲ
REVERSED LUNATE SIGMA SYMBOL	Ͻ ͻ	U+03FD U+037B	Ͻ ͻ
DOTTED LUNATE SIGMA SYMBOL	Ͼ ͼ	U+03FE U+037C	Ͼ ͼ
REVERSED DOTTED LUNATE SIGMA SYMBOL	Ͽ ͽ	U+03FF U+037D	Ͽ ͽ

There are several Unicode

Unicode

Unicode is a computing industry standard for the consistent encoding, representation and handling of text expressed in most of the world's writing systems...

 codepoints representing the Greek letter sigma.

The use of multiple codepoints for final / non-final sigma is somewhat unusual in Unicode. However, the two cannot always be distinguished by a simple algorithm (there are exceptions for abbreviations), and there is a significant history of them being separate characters in other specifications.

Additionally, there are at least 23 codepoints for sigma as a symbol (bold, italic, sans-serif, lunate, reversed, or dotted, in various combinations).

See also

• Antisigma
• Greek letters used in mathematics, science, and engineering
• Sampi
  Sampi
  Sampi is an archaic letter of the Greek alphabet. It was used in addition to the classical 24 letters of the alphabet to denote some type of a sibilant sound, probably or , in some eastern Ionic dialects of ancient Greek in the 6th and 5th centuries BC...