
Size homotopy group
Encyclopedia
The concept of size homotopy group is analogous in size theory of the classical concept of homotopy group
. In order to give its definition, let us assume that a size pair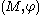 is given, where
is given, where 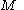 is a closed manifold
is a closed manifold
of class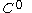 and
and 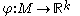 is a continuous function
is a continuous function
. Let us consider the partial order in
in 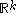 defined by setting
defined by setting 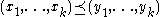 if and only if
if and only if  . For every
. For every 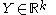 we set
we set  .
.
Assume that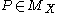 and
and  . If
. If  ,
,  are two paths from
are two paths from  to
to 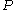 and a homotopy
and a homotopy
from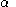 to
to  , based at
, based at 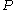 , exists in the topological space
, exists in the topological space
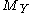 , then we write
, then we write 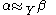 . The first size homotopy group of the size pair
. The first size homotopy group of the size pair 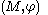 computed at
computed at 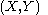 is defined to be the quotient set of the set of all path
is defined to be the quotient set of the set of all path
s from to
to 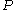 in
in 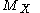 with respect to the equivalence relation
with respect to the equivalence relation
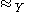 , endowed with the operation induced by the usual composition of based loop
, endowed with the operation induced by the usual composition of based loop
s .
In other words, the first size homotopy group of the size pair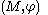 computed at
computed at 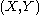 and
and 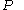 is the image
is the image
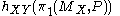
of the first homotopy group
 with base point
with base point 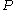 of the topological space
of the topological space
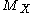 , when
, when 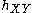 is the homomorphism
is the homomorphism
induced by the inclusion of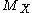 in
in 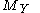 .
.
The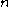 -th size homotopy group is obtained by substituting the loop
-th size homotopy group is obtained by substituting the loop
s based at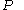 with the continuous function
with the continuous function
s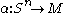 taking a fixed point of
taking a fixed point of 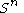 to
to 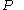 , as happens when higher homotopy group
, as happens when higher homotopy group
s are defined.
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
. In order to give its definition, let us assume that a size pair
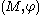 is given, where
is given, where 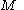 is a closed manifold
is a closed manifoldClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
of class
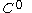 and
and 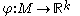 is a continuous function
is a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
. Let us consider the partial order
 in
in 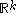 defined by setting
defined by setting 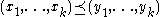 if and only if
if and only if  . For every
. For every 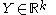 we set
we set  .
.Assume that
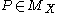 and
and  . If
. If  ,
,  are two paths from
are two paths from  to
to 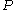 and a homotopy
and a homotopyHomotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
from
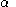 to
to  , based at
, based at 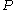 , exists in the topological space
, exists in the topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
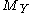 , then we write
, then we write 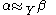 . The first size homotopy group of the size pair
. The first size homotopy group of the size pair 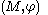 computed at
computed at 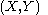 is defined to be the quotient set of the set of all path
is defined to be the quotient set of the set of all pathPath
Path, pathway or PATH may refer to:-Path:* Course , the intended path of a vehicle over the surface of the Earth* Trail, hiking trail, footpath, or bridle path...
s from
 to
to 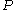 in
in 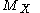 with respect to the equivalence relation
with respect to the equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
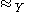 , endowed with the operation induced by the usual composition of based loop
, endowed with the operation induced by the usual composition of based loopLoop
- Technology :*Loop , sending a signal on a channel and receiving it back at the sending terminal*Loop , a method of control flow in computer science*Loop device, a Unix device node that allows a file to be mounted on a directory...
s .
In other words, the first size homotopy group of the size pair
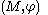 computed at
computed at 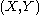 and
and 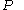 is the image
is the image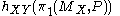
of the first homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
 with base point
with base point 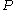 of the topological space
of the topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
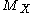 , when
, when 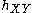 is the homomorphism
is the homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
induced by the inclusion of
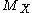 in
in 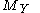 .
.The
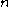 -th size homotopy group is obtained by substituting the loop
-th size homotopy group is obtained by substituting the loopLoop
- Technology :*Loop , sending a signal on a channel and receiving it back at the sending terminal*Loop , a method of control flow in computer science*Loop device, a Unix device node that allows a file to be mounted on a directory...
s based at
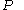 with the continuous function
with the continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s
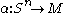 taking a fixed point of
taking a fixed point of 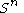 to
to 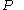 , as happens when higher homotopy group
, as happens when higher homotopy groupHomotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s are defined.

