
Size pair
Encyclopedia
In size theory, a size pair is a pair 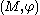 , where
, where 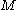 is a compact topological space
is a compact topological space
and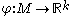 is a continuous function
is a continuous function
.
The function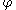 is called a measuring function. The topological space
is called a measuring function. The topological space 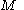 is usually assumed to be also a locally connected and Hausdorff space
is usually assumed to be also a locally connected and Hausdorff space
.
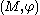 , where
, where 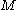 is a compact topological space
is a compact topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
and
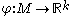 is a continuous function
is a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
.
The function
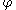 is called a measuring function. The topological space
is called a measuring function. The topological space 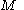 is usually assumed to be also a locally connected and Hausdorff space
is usually assumed to be also a locally connected and Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
See also
- Size theory
- Size functionSize functionSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
- Size functorSize functorGiven a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
- Size homotopy group
- Natural pseudodistanceNatural pseudodistanceIn size theory, the natural pseudodistance between two size pairs \ , \ is the value \inf_h \|\varphi-\psi\circ h\|_\infty\ , where h\ varies in the set of all homeomorphisms from the manifold M\ to the manifold N\ and \|\cdot\|_\infty\ is the supremum norm...

