
Size function
Encyclopedia
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane 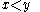 to the natural numbers, counting certain connected components of a topological space
to the natural numbers, counting certain connected components of a topological space
. They are used in pattern recognition
and topology
.
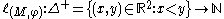 associated with the size pair
associated with the size pair 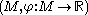 is defined in the following way. For every
is defined in the following way. For every 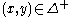 ,
, 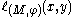 is equal to the number of connected components of the set
is equal to the number of connected components of the set
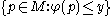 that contain at least one point at which the measuring function (a continuous function
that contain at least one point at which the measuring function (a continuous function
from a topological space
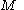 to
to 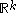 . )
. ) 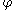 takes a value smaller than or equal to
takes a value smaller than or equal to 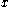
. The concept of size function can be easily extended to the case of a measuring function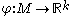 , where
, where 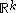 is endowed with the usual partial order
is endowed with the usual partial order
.
A survey about size functions (and size theory) can be found in
.

for the particular case of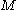 equal to the topological space of all piecewise
equal to the topological space of all piecewise 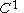 closed paths in a
closed paths in a 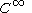 closed manifold
closed manifold
embedded in a Euclidean space. Here the topology on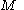 is induced by the
is induced by the
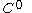 -norm, while the measuring function
-norm, while the measuring function 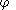 takes each path
takes each path 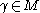 to its length.
to its length.
In
the case of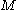 equal to the topological space of all ordered
equal to the topological space of all ordered 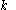 -tuples of points in a submanifold of a Euclidean space is considered.
-tuples of points in a submanifold of a Euclidean space is considered.
Here the topology on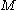 is induced by the metric
is induced by the metric 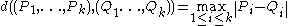 .
.
An extension of the concept of size function to algebraic topology
was made in
,
where the concept of size homotopy group was introduced. Here measuring functions taking values in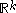 are allowed.
are allowed.
An extension to homology theory
(the size functor
) was introduced in
.
The concepts of size homotopy group and size functor
are strictly related to the concept of persistent homology group
,
studied in persistent homology. It is worth to point out that the size function is the rank of the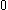 -th persistent homology group, while the relation between the persistent homology group
-th persistent homology group, while the relation between the persistent homology group
and the size homotopy group is analogous to the one existing between homology groups and homotopy group
s.
Size functions have been initially introduced as a mathematical tool for shape comparison in computer vision
and pattern recognition
, and have constituted the seed of size theory
,
,
,
,
,
,
,
The main point is that size functions are invariant for every transformation preserving the measuring function. Hence, they can be adapted to many different applications, by simply changing the measuring function in order to get the wanted invariance. Moreover, size functions show properties of relative resistance to noise, depending on the fact that they distribute the information all over the half-plane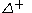 .
.
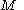 is a compact locally connected Hausdorff space. The following statements hold:
is a compact locally connected Hausdorff space. The following statements hold:
¤ every size function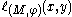 is a non-decreasing function in the variable
is a non-decreasing function in the variable 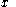 and a non-increasing function in the variable
and a non-increasing function in the variable 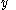 .
.
¤ every size function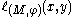 is locally right-constant in both its variables.
is locally right-constant in both its variables.
¤ for every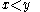 ,
, 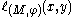 is finite.
is finite.
¤ for every and every
and every 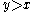 ,
, 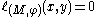 .
.
¤ for every and every
and every 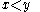 ,
, 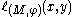 equals the number of connected components of
equals the number of connected components of 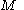 on which the minimum value of
on which the minimum value of 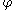 is smaller than or equal to
is smaller than or equal to 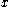 .
.
If we also assume that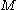 is a smooth closed manifold
is a smooth closed manifold
and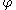 is a
is a 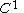 -function, the following useful property holds:
-function, the following useful property holds:
¤ in order that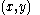 is a discontinuity point for
is a discontinuity point for 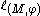 it is necessary that either
it is necessary that either 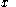 or
or 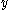 or both are critical values for
or both are critical values for 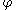 .
.
A strong link between the concept of size function and the concept of natural pseudodistance
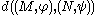 between the size pairs
between the size pairs 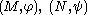 exists
exists
,
¤ if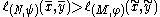 then
then 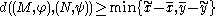 .
.
The previous result gives an easy way to get lower bounds for the natural pseudodistance
and is one of the main motivation to introduce the concept of size function.
functions in terms of collections of points and lines in the real plane with
multiplicities, i.e. as particular formal series, was furnished in
,
,
.
The points (called cornerpoints) and lines (called cornerlines) of such formal series encode the information about
discontinuities of the corresponding size functions, while
their multiplicities contain the information about the values taken by the
size function.
Formally:
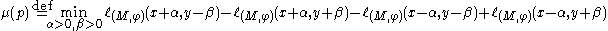
is positive.
The number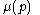 is said to be the multiplicity of
is said to be the multiplicity of 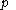 .
.
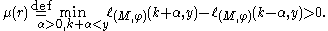
The number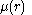 is sad to be the multiplicity of
is sad to be the multiplicity of 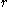 .
.
This representation contains the
same amount of information about the shape under study as the original
size function does, but is much more concise.
This algebraic approach to size functions leads to the definition of new similarity measures
between shapes, by translating the problem of comparing size functions into
the problem of comparing formal series. The most studied among these metrics between size function is the matching distance
.
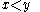 to the natural numbers, counting certain connected components of a topological space
to the natural numbers, counting certain connected components of a topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. They are used in pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
and topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
.
Formal definition
In size theory, the size function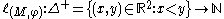 associated with the size pair
associated with the size pair 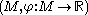 is defined in the following way. For every
is defined in the following way. For every 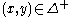 ,
, 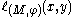 is equal to the number of connected components of the set
is equal to the number of connected components of the set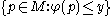 that contain at least one point at which the measuring function (a continuous function
that contain at least one point at which the measuring function (a continuous functionContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
from a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
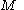 to
to 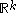 . )
. ) 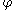 takes a value smaller than or equal to
takes a value smaller than or equal to 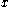
. The concept of size function can be easily extended to the case of a measuring function
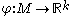 , where
, where 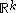 is endowed with the usual partial order
is endowed with the usual partial order.
A survey about size functions (and size theory) can be found in
.

History and applications
Size functions were introduced infor the particular case of
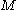 equal to the topological space of all piecewise
equal to the topological space of all piecewise 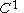 closed paths in a
closed paths in a 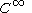 closed manifold
closed manifoldClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
embedded in a Euclidean space. Here the topology on
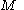 is induced by the
is induced by the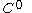 -norm, while the measuring function
-norm, while the measuring function 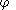 takes each path
takes each path 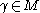 to its length.
to its length.In
the case of
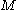 equal to the topological space of all ordered
equal to the topological space of all ordered 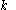 -tuples of points in a submanifold of a Euclidean space is considered.
-tuples of points in a submanifold of a Euclidean space is considered.Here the topology on
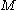 is induced by the metric
is induced by the metric 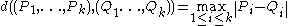 .
.An extension of the concept of size function to algebraic topology
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
was made in
,
where the concept of size homotopy group was introduced. Here measuring functions taking values in
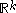 are allowed.
are allowed.An extension to homology theory
Homology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
(the size functor
Size functor
Given a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
) was introduced in
.
The concepts of size homotopy group and size functor
Size functor
Given a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
are strictly related to the concept of persistent homology group
,
studied in persistent homology. It is worth to point out that the size function is the rank of the
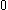 -th persistent homology group, while the relation between the persistent homology group
-th persistent homology group, while the relation between the persistent homology groupand the size homotopy group is analogous to the one existing between homology groups and homotopy group
Homotopy group
In mathematics, homotopy groups are used in algebraic topology to classify topological spaces. The first and simplest homotopy group is the fundamental group, which records information about loops in a space...
s.
Size functions have been initially introduced as a mathematical tool for shape comparison in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
and pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
, and have constituted the seed of size theory
,
,
,
,
,
,
,
The main point is that size functions are invariant for every transformation preserving the measuring function. Hence, they can be adapted to many different applications, by simply changing the measuring function in order to get the wanted invariance. Moreover, size functions show properties of relative resistance to noise, depending on the fact that they distribute the information all over the half-plane
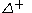 .
.Main properties
Assume that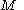 is a compact locally connected Hausdorff space. The following statements hold:
is a compact locally connected Hausdorff space. The following statements hold:¤ every size function
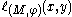 is a non-decreasing function in the variable
is a non-decreasing function in the variable 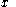 and a non-increasing function in the variable
and a non-increasing function in the variable 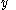 .
.¤ every size function
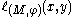 is locally right-constant in both its variables.
is locally right-constant in both its variables.¤ for every
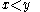 ,
, 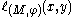 is finite.
is finite.¤ for every
 and every
and every 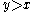 ,
, 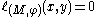 .
.¤ for every
 and every
and every 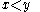 ,
, 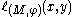 equals the number of connected components of
equals the number of connected components of 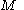 on which the minimum value of
on which the minimum value of 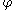 is smaller than or equal to
is smaller than or equal to 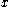 .
.If we also assume that
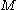 is a smooth closed manifold
is a smooth closed manifoldClosed manifold
In mathematics, a closed manifold is a type of topological space, namely a compact manifold without boundary. In contexts where no boundary is possible, any compact manifold is a closed manifold....
and
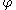 is a
is a 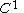 -function, the following useful property holds:
-function, the following useful property holds:¤ in order that
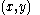 is a discontinuity point for
is a discontinuity point for 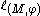 it is necessary that either
it is necessary that either 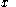 or
or 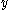 or both are critical values for
or both are critical values for 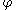 .
.A strong link between the concept of size function and the concept of natural pseudodistance
Natural pseudodistance
In size theory, the natural pseudodistance between two size pairs \ , \ is the value \inf_h \|\varphi-\psi\circ h\|_\infty\ , where h\ varies in the set of all homeomorphisms from the manifold M\ to the manifold N\ and \|\cdot\|_\infty\ is the supremum norm...
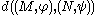 between the size pairs
between the size pairs 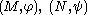 exists
exists,
¤ if
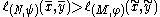 then
then 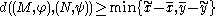 .
.The previous result gives an easy way to get lower bounds for the natural pseudodistance
Natural pseudodistance
In size theory, the natural pseudodistance between two size pairs \ , \ is the value \inf_h \|\varphi-\psi\circ h\|_\infty\ , where h\ varies in the set of all homeomorphisms from the manifold M\ to the manifold N\ and \|\cdot\|_\infty\ is the supremum norm...
and is one of the main motivation to introduce the concept of size function.
Representation by formal series
An algebraic representation of sizefunctions in terms of collections of points and lines in the real plane with
multiplicities, i.e. as particular formal series, was furnished in
,
,
.
The points (called cornerpoints) and lines (called cornerlines) of such formal series encode the information about
discontinuities of the corresponding size functions, while
their multiplicities contain the information about the values taken by the
size function.
Formally:
- cornerpoints are defined as those points
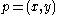 , with
, with 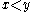 , such that the number
, such that the number
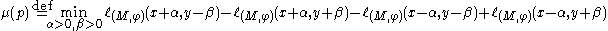
is positive.
The number
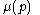 is said to be the multiplicity of
is said to be the multiplicity of 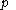 .
.- cornerlines and are defined as those lines
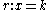 such that
such that
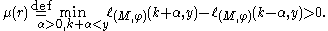
The number
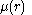 is sad to be the multiplicity of
is sad to be the multiplicity of 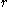 .
.- Representation Theorem: For every
 , it holds
, it holds 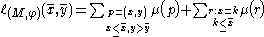
This representation contains the
same amount of information about the shape under study as the original
size function does, but is much more concise.
This algebraic approach to size functions leads to the definition of new similarity measures
between shapes, by translating the problem of comparing size functions into
the problem of comparing formal series. The most studied among these metrics between size function is the matching distance
Matching distance
In mathematics, the matching distance is a metric on the space of size functions.The core of the definition of matching distance is the observation that the...
.
See also
- Size theory
- Natural pseudodistanceNatural pseudodistanceIn size theory, the natural pseudodistance between two size pairs \ , \ is the value \inf_h \|\varphi-\psi\circ h\|_\infty\ , where h\ varies in the set of all homeomorphisms from the manifold M\ to the manifold N\ and \|\cdot\|_\infty\ is the supremum norm...
- Size functorSize functorGiven a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
- Size homotopy group
- Size pair
- Matching distanceMatching distanceIn mathematics, the matching distance is a metric on the space of size functions.The core of the definition of matching distance is the observation that the...
- Topological data analysisTopological data analysisTopological data analysis is a new area of study aimed at having applications in areas such as data mining and computer vision.The main problems are:# how one infers high-dimensional structure from low-dimensional representations; and...

