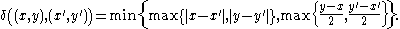Matching distance
Encyclopedia
In mathematics
, the matching distance is a metric
on the space of size function
s.
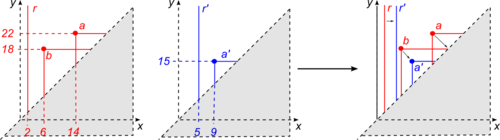 The core of the definition of matching distance is the observation that the
The core of the definition of matching distance is the observation that the
information contained in a size function can be combinatorially stored in a formal series of lines and points of the plane, called respectively cornerlines
and cornerpoints
.
Given two size functions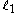 and
and  , let
, let 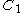 (resp.
(resp. 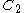 ) be the multiset of
) be the multiset of
all cornerpoints and cornerlines for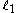 (resp.
(resp. 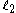 ) counted with their
) counted with their
multiplicities, augmented by adding a countable infinity of points of the
diagonal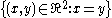 .
.
The matching distance between and
and 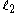 is given by
is given by
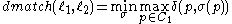
where varies among all the bijections between
varies among all the bijections between 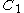 and
and  and
and
Roughly speaking, the matching distance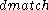
between two size functions is the minimum, over all the matchings
between the cornerpoints of the two size functions, of the maximum
of the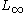 -distances between two matched cornerpoints. Since
-distances between two matched cornerpoints. Since
two size functions can have a different number of cornerpoints,
these can be also matched to points of the diagonal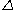 . Moreover, the definition of
. Moreover, the definition of 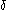 implies that matching two points of the diagonal has no cost.
implies that matching two points of the diagonal has no cost.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the matching distance is a metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on the space of size function
Size function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
s.

information contained in a size function can be combinatorially stored in a formal series of lines and points of the plane, called respectively cornerlines
Size function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
and cornerpoints
Size function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
.
Given two size functions
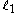 and
and  , let
, let 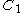 (resp.
(resp. 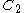 ) be the multiset of
) be the multiset ofall cornerpoints and cornerlines for
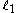 (resp.
(resp. 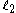 ) counted with their
) counted with theirmultiplicities, augmented by adding a countable infinity of points of the
diagonal
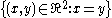 .
.The matching distance between
 and
and 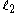 is given by
is given by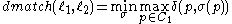
where
 varies among all the bijections between
varies among all the bijections between 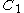 and
and  and
andRoughly speaking, the matching distance
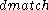
between two size functions is the minimum, over all the matchings
between the cornerpoints of the two size functions, of the maximum
of the
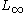 -distances between two matched cornerpoints. Since
-distances between two matched cornerpoints. Sincetwo size functions can have a different number of cornerpoints,
these can be also matched to points of the diagonal
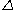 . Moreover, the definition of
. Moreover, the definition of 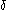 implies that matching two points of the diagonal has no cost.
implies that matching two points of the diagonal has no cost.See also
- Size theory
- Size functionSize functionSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane xSize functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane...
- Size functorSize functorGiven a size pair \ where M\ is a manifold of dimensionn\ and f\ is an arbitrary real continuous function definedon it, the i\ -th size functor, with i=0,\ldots,n\ , denoted...
- Size homotopy group
- Natural pseudodistanceNatural pseudodistanceIn size theory, the natural pseudodistance between two size pairs \ , \ is the value \inf_h \|\varphi-\psi\circ h\|_\infty\ , where h\ varies in the set of all homeomorphisms from the manifold M\ to the manifold N\ and \|\cdot\|_\infty\ is the supremum norm...