Small angle approximation
Encyclopedia
The small-angle approximation is a useful simplification of the basic trigonometric functions which is approximately true in the limit
where the angle approaches zero. They are truncations of the Taylor series
for the basic trigonometric functions to a second-order approximation
. This truncation gives:


 ,
,
where θ is the angle in radians.
The small angle approximation is useful in many areas of physics, including mechanics
, electromagnetics, optics
(where it forms the basis of the paraxial approximation
), cartography
, astronomy
, and so on.
 helps to trim the red away.
helps to trim the red away.
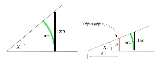
The opposite leg, O, is approximately equal to the length of the blue arc, s. Gathering facts from geometry, s = A*θ, from trigonometry, sin θ = O/H and tan θ = O/A, and from the picture, and
and  leads to:
leads to:
 .
.
Simplifying leaves,
 .
.



where θ is the angle and Bs are Bernoulli numbers.
When the angle θ is less than one radian, its powers θ2, θ3, ... decrease rapidly, so only a few are needed. The highest power included is called the order of the approximation. Neither sin θ nor tan θ has an θ2 term, so their first- and second-order approximations are the same. Truncating the functions to the second order gives:


 .
.
where X is measured in arcseconds.
The number 206,265 is approximately equal to the number of arcseconds in a circle
(1,296,000), divided by 2π.
The exact formula is
and the above approximation follows when tan(X) is replaced by X.
When calculating the period of a simple pendulum, the small-angle approximation for sine is used to allow the resulting differential equation to be solved easily by comparison with the differential equation describing simple harmonic motion
.
used in air navigation
has its basis in the small-angle approximation, plus the fact that one radian is approximately 60 degrees.
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
where the angle approaches zero. They are truncations of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
for the basic trigonometric functions to a second-order approximation
Orders of approximation
In science, engineering, and other quantitative disciplines, orders of approximation refer to formal or informal terms for how precise an approximation is, and to indicate progressively more refined approximations: in increasing order of precision, a zeroth order approximation, a first order...
. This truncation gives:


 ,
,where θ is the angle in radians.
The small angle approximation is useful in many areas of physics, including mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, electromagnetics, optics
Optics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
(where it forms the basis of the paraxial approximation
Paraxial approximation
In geometric optics, the paraxial approximation is a small-angle approximation used in Gaussian optics and ray tracing of light through an optical system ....
), cartography
Cartography
Cartography is the study and practice of making maps. Combining science, aesthetics, and technique, cartography builds on the premise that reality can be modeled in ways that communicate spatial information effectively.The fundamental problems of traditional cartography are to:*Set the map's...
, astronomy
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
, and so on.
Graphic
The accuracy of the approximations can be seen below in Figure 1 and Figure 2. As the angle approaches zero, it is clear that the gap between the approximation and the original function quickly vanishes.Geometric
The red section on the right, d, is the difference between the lengths of the hypotenuse, H, and the adjacent side, A. As is shown, H and A are almost the same length, meaning cos θ is close to 1 and helps to trim the red away.
helps to trim the red away.
The opposite leg, O, is approximately equal to the length of the blue arc, s. Gathering facts from geometry, s = A*θ, from trigonometry, sin θ = O/H and tan θ = O/A, and from the picture,
 and
and  leads to:
leads to: .
.Simplifying leaves,
 .
.Mathematical
The Taylor series about 0 of the trigonometric functions are


where θ is the angle and Bs are Bernoulli numbers.
When the angle θ is less than one radian, its powers θ2, θ3, ... decrease rapidly, so only a few are needed. The highest power included is called the order of the approximation. Neither sin θ nor tan θ has an θ2 term, so their first- and second-order approximations are the same. Truncating the functions to the second order gives:


 .
.Error of the approximations
Figure 3 shows the relative errors of the small angle approximations. The angles at which the relative error exceeds 1% are as follows:- tan θ ≈ θ at about 0.176 radians.
- sin θ ≈ θ at about 0.244 radians.
- cos θ ≈ 1 - θ2/2 at about 0.664 radians.
Astronomy
In astronomy, the angle subtended by the image of a distant object is often only a few arcseconds, so it is well suited to the small angle approximation. The linear size (D) is related to the angular size (X) and the distance from the observer (d) by the simple formula- D = X · d / 206,265
where X is measured in arcseconds.
The number 206,265 is approximately equal to the number of arcseconds in a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
(1,296,000), divided by 2π.
The exact formula is
- D = 2 d tan(X·π/1,296,000)
and the above approximation follows when tan(X) is replaced by X.
Motion of a pendulum
The second order Cos approximation is especially useful in calculating the potential energy of a pendulum, which can then be applied with a Lagrangian to find the indirect (energy) equation of motion.When calculating the period of a simple pendulum, the small-angle approximation for sine is used to allow the resulting differential equation to be solved easily by comparison with the differential equation describing simple harmonic motion
Simple harmonic motion
Simple harmonic motion can serve as a mathematical model of a variety of motions, such as the oscillation of a spring. Additionally, other phenomena can be approximated by simple harmonic motion, including the motion of a simple pendulum and molecular vibration....
.
Structural mechanics
The small angle approximation also appears in structural mechanics especially in stability and bifurcation analyses (mainly of axially-loaded columns ready to undergo buckling) leading to significant simplifications, though at a cost in accuracy and insight into the true behaviour.Piloting
The 1 in 60 rule1 in 60 rule
The 1 in 60 rule is used in air navigation, and states that if a pilot has travelled sixty miles then an error in track of one mile is approximately a 1° error. It is based on the small-angle approximation. In reality the error is 0.96° but this difference is trivial in air navigation. It is hard...
used in air navigation
Air navigation
The basic principles of air navigation are identical to general navigation, which includes the process of planning, recording, and controlling the movement of a craft from one place to another....
has its basis in the small-angle approximation, plus the fact that one radian is approximately 60 degrees.
See also
- Skinny triangleSkinny triangleA skinny triangle in trigonometry is a triangle whose height is much greater than its base. The solution of such triangles can be greatly simplified by using the approximation that the sine of a small angle is equal to the angle in radians...
- Infinitesimal oscillations of a pendulum

