
Specific relative angular momentum
Encyclopedia
The specific relative angular momentum (h) is also known as the areal momentum (defined as the product of mass and areal velocity
).
In astrodynamics
, the specific relative angular momentum of two orbiting bodies
is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum
divided by the reduced mass
. Specific relative angular momentum plays a pivotal role in the analysis of the two-body problem
.
 , is defined as the cross product
, is defined as the cross product
of the relative position vector and the relative velocity vector
and the relative velocity vector  .
.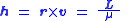
where:
The units of are m2s−1.
are m2s−1.
For unperturbed orbits the vector is always perpendicular to the fixed orbital plane
vector is always perpendicular to the fixed orbital plane
. However, for perturbed orbits the vector is generally not perpendicular to the osculating orbital plane
vector is generally not perpendicular to the osculating orbital plane
As usual in physics, the magnitude
of the vector quantity is denoted by
is denoted by  :
:
Since the area of the entire orbital ellipse is swept out in one orbital period
, is equal to twice the area of the ellipse divided by the orbital period, giving the equation
is equal to twice the area of the ellipse divided by the orbital period, giving the equation
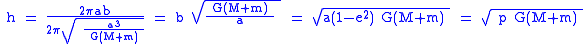 .
.
where
Areal velocity
Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
).
In astrodynamics
Astrodynamics
Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...
, the specific relative angular momentum of two orbiting bodies
Orbiting body
In astrodynamics, an orbiting body is a body that orbits a primary body .The orbiting body is properly referred to as the secondary body.It is less massive than the primary body ....
is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
divided by the reduced mass
Reduced mass
Reduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
. Specific relative angular momentum plays a pivotal role in the analysis of the two-body problem
Two-body problem
In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...
.
Definition
Specific relative angular momentum, represented by the symbol , is defined as the cross product
, is defined as the cross productCross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
of the relative position vector
 and the relative velocity vector
and the relative velocity vector  .
.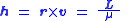
where:
 is the relative orbital position vector
is the relative orbital position vector is the relative orbital velocity vector
is the relative orbital velocity vector is the total angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
is the total angular momentumAngular momentumIn physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
of the system is the reduced massReduced massReduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
is the reduced massReduced massReduced mass is the "effective" inertial mass appearing in the two-body problem of Newtonian mechanics. This is a quantity with the unit of mass, which allows the two-body problem to be solved as if it were a one-body problem. Note however that the mass determining the gravitational force is not...
The units of
 are m2s−1.
are m2s−1.For unperturbed orbits the
 vector is always perpendicular to the fixed orbital plane
vector is always perpendicular to the fixed orbital planeOrbital plane
Orbital plane may refer to:*Orbital plane *In anatomy, it refers to a specific area of the maxilla...
. However, for perturbed orbits the
 vector is generally not perpendicular to the osculating orbital plane
vector is generally not perpendicular to the osculating orbital planeOsculating orbit
In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space is the gravitational Kepler orbit In astronomy, and in particular in astrodynamics, the osculating orbit of an object in space (at a given moment of time) is the gravitational Kepler orbit In astronomy,...
As usual in physics, the magnitude
Magnitude (mathematics)
The magnitude of an object in mathematics is its size: a property by which it can be compared as larger or smaller than other objects of the same kind; in technical terms, an ordering of the class of objects to which it belongs....
of the vector quantity
 is denoted by
is denoted by  :
:
Elliptical orbit
In an elliptical orbit, the specific relative angular momentum is twice the area per unit time swept out by a chord from the primary to the secondary: this area is referred to by Kepler's second law of planetary motion.Since the area of the entire orbital ellipse is swept out in one orbital period
Orbital period
The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...
,
 is equal to twice the area of the ellipse divided by the orbital period, giving the equation
is equal to twice the area of the ellipse divided by the orbital period, giving the equation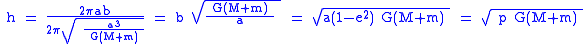 .
.where
 is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
is the semi-major axisSemi-major axisThe major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape... is the semi-minor axisSemi-minor axisIn geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...
is the semi-minor axisSemi-minor axisIn geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis... is the semi-latus rectum
is the semi-latus rectum is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is the gravitational constantGravitational constantThe gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal... ,
,  are the two masses.
are the two masses.

