
Stable vector bundle
Encyclopedia
In mathematics, a stable vector bundle is a vector bundle
that is stable in the sense of geometric invariant theory
. They were defined by .
(or over a Riemann surface
) is stable if and only if

for all proper non-zero subbundles V of W
and is semistable if

for all proper non-zero subbundles V of W. Informally this says that a bundle is stable if it is "more ample" than any proper subbundle, and is unstable if it contains a "more ample" subbundle.
The moduli space of stable bundles of given rank and degree is an algebraic variety
.
showed that stable bundles on projective nonsingular curves are the same as those that have projectively flat unitary irreducible connections; these correspond to irreducible unitary representations of the fundamental group. Kobayashi and Hitchin
conjectured an analogue of this in higher dimensions; this was proved for projective nonsingular surfaces by , who showed that in this case a vector bundle is stable if and only if it has an irreducible Hermitian-Einstein connection.
The cohomology
of the moduli space
of stable vector bundles over a curve was described by and .

for all proper non-zero subbundles (or subsheaves) V of W, where denotes the Euler characteristic of an algebraic vector bundle and the vector bundle
denotes the Euler characteristic of an algebraic vector bundle and the vector bundle 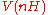 means the n-th twist of V by H. W is called semistable if the above holds with < replaced by ≤.
means the n-th twist of V by H. W is called semistable if the above holds with < replaced by ≤.
There are also other variants in the literature: cf. this thesis p.29.
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
that is stable in the sense of geometric invariant theory
Geometric invariant theory
In mathematics Geometric invariant theory is a method for constructing quotients by group actions in algebraic geometry, used to construct moduli spaces...
. They were defined by .
Stable vector bundles over curves
A bundle W over an algebraic curveAlgebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
(or over a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
) is stable if and only if

for all proper non-zero subbundles V of W
and is semistable if

for all proper non-zero subbundles V of W. Informally this says that a bundle is stable if it is "more ample" than any proper subbundle, and is unstable if it contains a "more ample" subbundle.
The moduli space of stable bundles of given rank and degree is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
.
showed that stable bundles on projective nonsingular curves are the same as those that have projectively flat unitary irreducible connections; these correspond to irreducible unitary representations of the fundamental group. Kobayashi and Hitchin
Nigel Hitchin
Nigel Hitchin is a British mathematician working in the fields of differential geometry, algebraic geometry, and mathematical physics.-Academic career:...
conjectured an analogue of this in higher dimensions; this was proved for projective nonsingular surfaces by , who showed that in this case a vector bundle is stable if and only if it has an irreducible Hermitian-Einstein connection.
The cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the moduli space
Moduli space
In algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of stable vector bundles over a curve was described by and .
Stable vector bundles over projective varieties
If X is a smooth projective variety of dimension n and H is a hyperplane section, then a vector bundle (or torsionfree sheaf) W is called stable if
for all proper non-zero subbundles (or subsheaves) V of W, where
 denotes the Euler characteristic of an algebraic vector bundle and the vector bundle
denotes the Euler characteristic of an algebraic vector bundle and the vector bundle 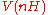 means the n-th twist of V by H. W is called semistable if the above holds with < replaced by ≤.
means the n-th twist of V by H. W is called semistable if the above holds with < replaced by ≤.There are also other variants in the literature: cf. this thesis p.29.

