String duality
Encyclopedia
String duality is a class of symmetries
in physics
that link different string theories
, theories which assume that the fundamental building blocks of the universe
are string
s instead of point particle
s.
Before the so-called "duality revolution" there were believed to be five distinct versions of string theory, plus the (unstable) bosonic and gluonic theories.
Note that in the type IIA and type IIB string theories closed strings are allowed to move everywhere throughout the ten-dimensional space-time (called the bulk), while open strings have their ends attached to D-brane
s, which are membranes of lower dimensionality (their dimension is odd - 1,3,5,7 or 9 - in type IIA and even - 0,2,4,6 or 8 - in type IIB, including the time direction).
Before the 1990s, string theorists believed there were five distinct superstring theories: type I, types IIA and IIB, and the two heterotic string
theories (SO(32) and E8×E8
). The thinking was that out of these five candidate theories, only one was the actual theory of everything
, and that theory was the theory whose low energy limit, with ten dimensions spacetime compactified
down to four, matched the physics observed in our world today. It is now known that the five superstring theories are not fundamental, but are instead different limits of a more fundamental theory, dubbed M-theory
. These theories are related by transformations called dualities. If two theories are related by a duality transformation, each observable of the first theory can be mapped in some way to the second theory to yield equivalent predictions. The two theories are then said to be dual to one another under that transformation. Put differently, the two theories are two mathematically different descriptions of the same phenomena. A simple example of a duality is the equivalence of particle physics
upon replacing matter with antimatter; describing our universe in terms of anti-particles would yield identical predictions for any possible experiment.
String dualities often link quantities that appear to be separate: Large and small distance scales, strong and weak coupling strengths. These quantities have always marked very distinct limits of behavior of a physical system, in both classical field theory
and quantum particle physics
. But strings can obscure the difference between large and small, strong and weak, and this is how these five very different theories end up being related.
around the circle, because its momentum is linked to its wavelength
(see Wave-particle duality), and 2πR must be a multiple of that. In fact, the particle momentum around the circle - and the contribution to its energy - is of the form n/R (in standard units
, for an integer n), so that at large R there will be many more states compared to small R (for a given maximum energy). A string, in addition to traveling around the circle, may also wrap around it. The number of times the string winds around the circle is called the winding number
, and that is also quantized (as it must be an integer). Winding around the circle requires energy, because the string must be stretched against its tension, so it contributes an amount of energy of the form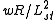
, where 
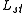is a constant called the string length and w is the winding number (an integer). Now (for a given maximum energy) there will be many different states (with different momenta) at large R, but there will also be many different states (with different windings) at small R. In fact, a theory with large R and a theory with small R are equivalent, where the role of momentum in the first is played by the winding in the second, and vice versa. Mathematically, taking R to 
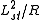and switching n and w will yield the same equations. So exchanging momentum and winding modes of the string exchanges a large distance scale with a small distance scale.
This type of duality is called T-duality
. T-duality relates type IIA superstring theory to type IIB superstring theory. That means if we take type IIA and Type IIB theory and compactify them both on a circle (one with a large radius and the other with a small radius) then switching the momentum and winding modes, and switching the distance scale, changes one theory into the other. The same is also true for the two heterotic theories. T-duality also relates type I superstring theory to both type IIA and type IIB superstring theories with certain boundary conditions (termed orientifold
).
Formally, the location of the string on the circle is described by two fields living on it, one which is left-moving and another which is right-moving. The movement of the string center (and hence its momentum) is related to the sum of the fields, while the string stretch (and hence its winding number) is related to their difference. T-duality can be formally described by taking the left-moving field to minus itself, so that the sum and the difference are interchanged, leading to switching of momentum and winding.
has a coupling constant
, which is a measure of its strength, and determines the chances of one particle to emit or absorb another particle. For electromagnetism
, the coupling constant is proportional to the square of the electric charge
. When physicists study the quantum behavior of electromagnetism
, they can't solve the whole theory exactly, because every particle may emit and absorb many other particles, which may also do the same, endlessly. So events of emission and absorption are considered as perturbations and are dealt with by a series of approximations, first assuming there is only one such event, then correcting the result for allowing two such events, etc (this method is called Perturbation theory
). This is a reasonable approximation only if the coupling constant is small, which is the case for electromagnetism. But if the coupling constant gets large, that method of calculation breaks down, and the little pieces become worthless as an approximation to the real physics.
This also can happen in string theory. String theories have a coupling constant. But unlike in particle theories, the string coupling constant is not just a number, but depends on one of the oscillation
modes of the string, called the dilaton
. Exchanging the dilaton field with minus itself exchanges a very large coupling constant with a very small one. This symmetry is called S-duality
. If two string theories are related by S-duality, then one theory with a strong coupling constant is the same as the other theory with weak coupling constant. The theory with strong coupling cannot be understood by means of perturbation theory
, but the theory with weak coupling can. So if the two theories are related by S-duality, then we just need to understand the weak theory, and that is equivalent to understanding the strong theory.
Superstring theories related by S-duality are: type I superstring theory with heterotic SO(32) superstring theory, and type IIB theory with itself.
Furthermore, type IIA theory in strong coupling behaves like an 11-dimensional theory, with the dilaton
field playing the role of an eleventh dimension. This 11-dimensional theory is known as M-theory
.
Unlike the T-duality, however, S-duality has not been proven to even a physics level of rigor for any of the aforementioned cases. It remains, strictly speaking, a conjecture, although most string theorists believe in its validity.
Symmetry in physics
In physics, symmetry includes all features of a physical system that exhibit the property of symmetry—that is, under certain transformations, aspects of these systems are "unchanged", according to a particular observation...
in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
that link different string theories
String theory
String theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
, theories which assume that the fundamental building blocks of the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
are string
String (physics)
A string is a hypothetical vibrating one-dimensional sub-atomic structure and one of the main objects of study in string theory, a branch of theoretical physics. There are different string theories, many of which are unified by M-theory. A string is an object with a one-dimensional spatial extent,...
s instead of point particle
Point particle
A point particle is an idealization of particles heavily used in physics. Its defining feature is that it lacks spatial extension: being zero-dimensional, it does not take up space...
s.
Before the so-called "duality revolution" there were believed to be five distinct versions of string theory, plus the (unstable) bosonic and gluonic theories.
| String Theories | ||
|---|---|---|
| Type | Spacetime dimensions |
Details |
| Bosonic | 26 | Only boson Boson In particle physics, bosons are subatomic particles that obey Bose–Einstein statistics. Several bosons can occupy the same quantum state. The word boson derives from the name of Satyendra Nath Bose.... s, no fermion Fermion In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics.... s means only forces, no matter, with both open and closed strings; major flaw: a particle Particle physics Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics... with imaginary mass Mass Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:... , called the tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , representing an instability in the theory. |
| I | 10 | Supersymmetry Supersymmetry In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners... between forces and matter, with both closed strings and open strings, no tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , group symmetry is SO(32) |
| IIA | 10 | Supersymmetry Supersymmetry In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners... between forces and matter, with closed strings and open strings bound to D-brane D-brane In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989... s, no tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , massless fermion Fermion In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics.... s spin both ways (nonchiral) |
| IIB | 10 | Supersymmetry Supersymmetry In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners... between forces and matter, with closed strings and open strings bound to D-brane D-brane In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989... s, no tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , massless fermion Fermion In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics.... s only spin one way (chiral) |
| HO | 10 | Supersymmetry Supersymmetry In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners... between forces and matter, with closed strings only, no tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , heterotic, meaning right moving and left moving strings differ, group symmetry is SO(32) |
| HE | 10 | Supersymmetry Supersymmetry In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners... between forces and matter, with closed strings only, no tachyon Tachyon A tachyon is a hypothetical subatomic particle that always moves faster than light. In the language of special relativity, a tachyon would be a particle with space-like four-momentum and imaginary proper time. A tachyon would be constrained to the space-like portion of the energy-momentum graph... , heterotic, meaning right moving and left moving strings differ, group symmetry is E8×E8 E8 (mathematics) In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8... |
Note that in the type IIA and type IIB string theories closed strings are allowed to move everywhere throughout the ten-dimensional space-time (called the bulk), while open strings have their ends attached to D-brane
D-brane
In string theory, D-branes are a class of extended objects upon which open strings can end with Dirichlet boundary conditions, after which they are named. D-branes were discovered by Dai, Leigh and Polchinski, and independently by Hořava in 1989...
s, which are membranes of lower dimensionality (their dimension is odd - 1,3,5,7 or 9 - in type IIA and even - 0,2,4,6 or 8 - in type IIB, including the time direction).
Before the 1990s, string theorists believed there were five distinct superstring theories: type I, types IIA and IIB, and the two heterotic string
Heterotic string
In physics, a heterotic string is a peculiar mixture of the bosonic string and the superstring...
theories (SO(32) and E8×E8
E8 (mathematics)
In mathematics, E8 is any of several closely related exceptional simple Lie groups, linear algebraic groups or Lie algebras of dimension 248; the same notation is used for the corresponding root lattice, which has rank 8...
). The thinking was that out of these five candidate theories, only one was the actual theory of everything
Theory of everything
A theory of everything is a putative theory of theoretical physics that fully explains and links together all known physical phenomena, and predicts the outcome of any experiment that could be carried out in principle....
, and that theory was the theory whose low energy limit, with ten dimensions spacetime compactified
Compactification (physics)
In physics, compactification means changing a theory with respect to one of its space-time dimensions. Instead of having a theory with this dimension being infinite, one changes the theory so that this dimension has a finite length, and may also be periodic....
down to four, matched the physics observed in our world today. It is now known that the five superstring theories are not fundamental, but are instead different limits of a more fundamental theory, dubbed M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
. These theories are related by transformations called dualities. If two theories are related by a duality transformation, each observable of the first theory can be mapped in some way to the second theory to yield equivalent predictions. The two theories are then said to be dual to one another under that transformation. Put differently, the two theories are two mathematically different descriptions of the same phenomena. A simple example of a duality is the equivalence of particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
upon replacing matter with antimatter; describing our universe in terms of anti-particles would yield identical predictions for any possible experiment.
String dualities often link quantities that appear to be separate: Large and small distance scales, strong and weak coupling strengths. These quantities have always marked very distinct limits of behavior of a physical system, in both classical field theory
Classical field theory
A classical field theory is a physical theory that describes the study of how one or more physical fields interact with matter. The word 'classical' is used in contrast to those field theories that incorporate quantum mechanics ....
and quantum particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
. But strings can obscure the difference between large and small, strong and weak, and this is how these five very different theories end up being related.
T-duality
Suppose we are in ten spacetime dimensions, which means we have nine space dimensions and one time. Take one of those nine space dimensions and make it a circle of radius R, so that traveling in that direction for a distance L = 2πR takes you around the circle and brings you back to where you started. A particle traveling around this circle will have a quantized momentumMomentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
around the circle, because its momentum is linked to its wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
(see Wave-particle duality), and 2πR must be a multiple of that. In fact, the particle momentum around the circle - and the contribution to its energy - is of the form n/R (in standard units
Standard units
Standard units may refer to:*Units of measurement*United States customary units...
, for an integer n), so that at large R there will be many more states compared to small R (for a given maximum energy). A string, in addition to traveling around the circle, may also wrap around it. The number of times the string winds around the circle is called the winding number
Winding number
In mathematics, the winding number of a closed curve in the plane around a given point is an integer representing the total number of times that curve travels counterclockwise around the point...
, and that is also quantized (as it must be an integer). Winding around the circle requires energy, because the string must be stretched against its tension, so it contributes an amount of energy of the form
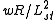, where 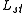is a constant called the string length and w is the winding number (an integer). Now (for a given maximum energy) there will be many different states (with different momenta) at large R, but there will also be many different states (with different windings) at small R. In fact, a theory with large R and a theory with small R are equivalent, where the role of momentum in the first is played by the winding in the second, and vice versa. Mathematically, taking R to 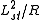and switching n and w will yield the same equations. So exchanging momentum and winding modes of the string exchanges a large distance scale with a small distance scale.This type of duality is called T-duality
T-duality
T-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
. T-duality relates type IIA superstring theory to type IIB superstring theory. That means if we take type IIA and Type IIB theory and compactify them both on a circle (one with a large radius and the other with a small radius) then switching the momentum and winding modes, and switching the distance scale, changes one theory into the other. The same is also true for the two heterotic theories. T-duality also relates type I superstring theory to both type IIA and type IIB superstring theories with certain boundary conditions (termed orientifold
Orientifold
In theoretical physics orientifold is a generalization of the notion of orbifold, proposed by Augusto Sagnotti in 1987. The novelty is that in the case of string theory the non-trivial element of the orbifold group includes the reversal of the orientation of the string...
).
Formally, the location of the string on the circle is described by two fields living on it, one which is left-moving and another which is right-moving. The movement of the string center (and hence its momentum) is related to the sum of the fields, while the string stretch (and hence its winding number) is related to their difference. T-duality can be formally described by taking the left-moving field to minus itself, so that the sum and the difference are interchanged, leading to switching of momentum and winding.
S-duality
Every forceForce
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
has a coupling constant
Coupling constant
In physics, a coupling constant, usually denoted g, is a number that determines the strength of an interaction. Usually the Lagrangian or the Hamiltonian of a system can be separated into a kinetic part and an interaction part...
, which is a measure of its strength, and determines the chances of one particle to emit or absorb another particle. For electromagnetism
Electromagnetism
Electromagnetism is one of the four fundamental interactions in nature. The other three are the strong interaction, the weak interaction and gravitation...
, the coupling constant is proportional to the square of the electric charge
Electric charge
Electric charge is a physical property of matter that causes it to experience a force when near other electrically charged matter. Electric charge comes in two types, called positive and negative. Two positively charged substances, or objects, experience a mutual repulsive force, as do two...
. When physicists study the quantum behavior of electromagnetism
Quantum electrodynamics
Quantum electrodynamics is the relativistic quantum field theory of electrodynamics. In essence, it describes how light and matter interact and is the first theory where full agreement between quantum mechanics and special relativity is achieved...
, they can't solve the whole theory exactly, because every particle may emit and absorb many other particles, which may also do the same, endlessly. So events of emission and absorption are considered as perturbations and are dealt with by a series of approximations, first assuming there is only one such event, then correcting the result for allowing two such events, etc (this method is called Perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
). This is a reasonable approximation only if the coupling constant is small, which is the case for electromagnetism. But if the coupling constant gets large, that method of calculation breaks down, and the little pieces become worthless as an approximation to the real physics.
This also can happen in string theory. String theories have a coupling constant. But unlike in particle theories, the string coupling constant is not just a number, but depends on one of the oscillation
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
modes of the string, called the dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
. Exchanging the dilaton field with minus itself exchanges a very large coupling constant with a very small one. This symmetry is called S-duality
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
. If two string theories are related by S-duality, then one theory with a strong coupling constant is the same as the other theory with weak coupling constant. The theory with strong coupling cannot be understood by means of perturbation theory
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
, but the theory with weak coupling can. So if the two theories are related by S-duality, then we just need to understand the weak theory, and that is equivalent to understanding the strong theory.
Superstring theories related by S-duality are: type I superstring theory with heterotic SO(32) superstring theory, and type IIB theory with itself.
Furthermore, type IIA theory in strong coupling behaves like an 11-dimensional theory, with the dilaton
Dilaton
In particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
field playing the role of an eleventh dimension. This 11-dimensional theory is known as M-theory
M-theory
In theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
.
Unlike the T-duality, however, S-duality has not been proven to even a physics level of rigor for any of the aforementioned cases. It remains, strictly speaking, a conjecture, although most string theorists believe in its validity.
See also
- DilatonDilatonIn particle physics, a dilaton is a hypothetical particle. It also appears in Kaluza-Klein theory's compactifications of extra dimensions when the volume of the compactified dimensions vary....
- M-theoryM-theoryIn theoretical physics, M-theory is an extension of string theory in which 11 dimensions are identified. Because the dimensionality exceeds that of superstring theories in 10 dimensions, proponents believe that the 11-dimensional theory unites all five string theories...
- S-dualityS-dualityIn theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
- StringString (physics)A string is a hypothetical vibrating one-dimensional sub-atomic structure and one of the main objects of study in string theory, a branch of theoretical physics. There are different string theories, many of which are unified by M-theory. A string is an object with a one-dimensional spatial extent,...
- String theoryString theoryString theory is an active research framework in particle physics that attempts to reconcile quantum mechanics and general relativity. It is a contender for a theory of everything , a manner of describing the known fundamental forces and matter in a mathematically complete system...
- T-dualityT-dualityT-duality is a symmetry of quantum field theories with differing classical descriptions, of which the relationship between small and large distances in various string theories is a special case. Discussion of the subject originated in a paper by T. S. Buscher and was further developed by Martin...
- U-dualityU-dualityIn physics, U-duality is a symmetry of string theory or M-theory combining S-duality and T-duality transformations. The term is most often met in the context of the "U-duality group" of M-theory as defined on a particular background space . This is the union of all the S- and T-dualities...