
Strong cardinal
Encyclopedia
In set theory
, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.
, κ is λ-strong means that κ is a cardinal number
and there exists an elementary embedding j from the universe V into a transitive inner model
M with critical point
κ and
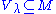
That is, M agrees with V on an initial segment. Then κ is strong means that it is λ-strong for all ordinals λ.
s in the consistency strength hierarchy.
They also lie below superstrong cardinals and Woodin cardinal
s. However, the least strong cardinal is larger than the least superstrong cardinal.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, a strong cardinal is a type of large cardinal. It is a weakening of the notion of a supercompact cardinal.
Formal definition
If λ is any ordinalOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
, κ is λ-strong means that κ is a cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
and there exists an elementary embedding j from the universe V into a transitive inner model
Inner model
In mathematical logic, suppose T is a theory in the languageL = \langle \in \rangleof set theory.If M is a model of L describing a set theory and N is a class of M such that \langle N, \in_M, \ldots \rangle...
M with critical point
Critical point (set theory)
In set theory, the critical point of an elementary embedding of a transitive class into another transitive class is the smallest ordinal which is not mapped to itself....
κ and
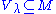
That is, M agrees with V on an initial segment. Then κ is strong means that it is λ-strong for all ordinals λ.
Relationship with other large cardinals
It is obvious from the definitions that strong cardinals lie below supercompact cardinals and above measurable cardinalMeasurable cardinal
- Measurable :Formally, a measurable cardinal is an uncountable cardinal number κ such that there exists a κ-additive, non-trivial, 0-1-valued measure on the power set of κ...
s in the consistency strength hierarchy.
They also lie below superstrong cardinals and Woodin cardinal
Woodin cardinal
In set theory, a Woodin cardinal is a cardinal number λ such that for all functionsthere exists a cardinal κ In set theory, a Woodin cardinal is a cardinal number λ such that for all functions...
s. However, the least strong cardinal is larger than the least superstrong cardinal.

