Strong prime
Encyclopedia
In mathematics
, a strong prime is a prime number
with certain special properties. The definitions of strong primes are different in cryptography
and number theory
.
, a prime number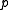
is strong if the following conditions are satisfied.
Sometimes a prime that satisfies a subset of the above conditions is also called strong. In some cases, some additional conditions may be included. For example,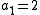
, or 
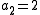, etc.
, a strong prime is a prime number that is greater than the arithmetic mean
of the nearest prime above and below (in other words, it's closer to the following than to the preceding prime). Or to put it algebraically, given a prime number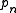
, where n is its index in the ordered set of prime numbers, 
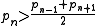. The first few strong primes are
For example, 17 is the seventh prime. The sixth and eighth primes, 13 and 19, add up to 32, and half that is 16. That is less than 17, thus 17 is a strong prime.
In a twin prime
pair (p, p + 2) with p > 5, p is always a strong prime, since 3 must divide p − 2 which cannot be prime.
It is possible for a prime to be a strong prime both in the cryptographic sense and the number theoretic sense. For the sake of illustration, 439351292910452432574786963588089477522344331 is a strong prime in the number theoretic sense because the arithmetic mean of its two neighboring primes is 62 less. Without the aid of a computer, this number would be a strong prime in the cryptographic sense because 439351292910452432574786963588089477522344330 has the large prime factor 1747822896920092227343 (and in turn the number one less than that has the large prime factor 1683837087591611009), 439351292910452432574786963588089477522344332 has the large prime factor 864608136454559457049 (and in turn the number one less than that has the large prime factor 105646155480762397). Even using algorithms more advanced than trial by division, these numbers would be difficult to factor by hand. For a modern computer algebra system
, these numbers can be factored almost instantaneously. A cryptographically strong prime has to be much larger than this example.
process in RSA cryptosystems, the modulus
should be chosen as the product of two strong primes. This makes the factorization of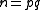 
using Pollard's p − 1 algorithm computationally infeasible. For this reason, strong primes are required by the ANSI X9.31 standard for use in generating RSA keys for digital signature
s. However, strong primes do not protect against modulus factorisation using newer algorithms such as Lenstra elliptic curve factorization
and Number Field Sieve algorithm. Given the additional cost of generating strong primes RSA Security
do not currently recommend their use in key generation
. Similar (and more technical) argument is also given by Rivest and Silverman .
in 1978 that if all the factors of p-1 are less than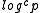
, then the problem of solving discrete logarithm
modulo p is in P. Therefore, for cryptosystems based on discrete logarithm, such as DSA
, it is required that p-1 have at least one large prime factor.
is likely to be a cryptographically strong prime.
Note that the criteria for determining if a pseudoprime is a strong pseudoprime
is by congruences to powers of a base, not by inequality to the arithmetic mean of neighboring pseudoprimes.
When a prime is equal to the mean of its neighboring primes, it's called a balanced prime. When it's less, it's called a weak prime.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a strong prime is a prime number
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
with certain special properties. The definitions of strong primes are different in cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
and number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
.
Definition in cryptography
In cryptographyCryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, a prime number
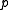is strong if the following conditions are satisfied.-
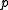is large. -
has large prime factors. That is,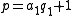 
for some integer 
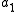and large prime 
. -
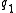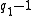has large prime factors. That is, 
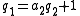for some integer 
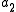and large prime 
. -
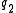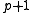has large prime factors. That is, 
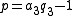for some integer 
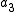and large prime 
.
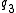Sometimes a prime that satisfies a subset of the above conditions is also called strong. In some cases, some additional conditions may be included. For example,
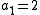, or 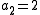, etc.Definition in number theory
In number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, a strong prime is a prime number that is greater than the arithmetic mean
Arithmetic mean
In mathematics and statistics, the arithmetic mean, often referred to as simply the mean or average when the context is clear, is a method to derive the central tendency of a sample space...
of the nearest prime above and below (in other words, it's closer to the following than to the preceding prime). Or to put it algebraically, given a prime number
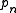, where n is its index in the ordered set of prime numbers, 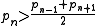. The first few strong primes are- 1111 (number)11 is the natural number following 10 and preceding 12.Eleven is the first number which cannot be counted with a human's eight fingers and two thumbs additively. In English, it is the smallest positive integer requiring three syllables and the largest prime number with a single-morpheme name...
, 1717 (number)17 is the natural number following 16 and preceding 18. It is prime.In spoken English, the numbers 17 and 70 are sometimes confused because they sound similar. When carefully enunciated, they differ in which syllable is stressed: 17 vs 70...
, 2929 (number)29 is the natural number following 28 and preceding 30.-In mathematics:It is the tenth prime number, and also the fourth primorial prime. It forms a twin prime pair with thirty-one, which is also a primorial prime. Twenty-nine is also the sixth Sophie Germain prime. It is also the sum of three...
, 3737 (number)37 is the natural number following 36 and preceding 38.-In mathematics:It is a prime number, the fifth lucky prime, the first irregular prime, the third unique prime and the third cuban prime of the form...
, 4141 (number)41 is the natural number following 40 and preceding 42.-In mathematics:Forty-one is the 13th smallest prime number. The next is forty-three, with which it comprises a twin prime...
, 5959 (number)59 is the natural number following 58 and preceding 60.-In mathematics:Fifty-nine is the 17th smallest prime number. The next is sixty-one, with which it comprises a twin prime. 59 is an irregular prime, a safe prime and the 14th supersingular prime. It is an Eisenstein prime with no imaginary...
, 6767 (number)67 is the natural number following 66 and preceding 68. It is an odd number.-In mathematics:Sixty-seven is the 19th prime number , an irregular prime, a lucky prime, the sum of five consecutive primes , and a Heegner number.Since 18! + 1 is divisible by 67 but 67 is not one more than a multiple of...
, 7171 (number)71 is the natural number following 70 and preceding 72.-In mathematics:71 is the algebraic degree of Conway's constant, a remarkable number arising in the study of look-and-say sequences....
, 7979 (number)Seventy-nine is the natural number following 78 and preceding 80.79 may represent:-In mathematics:*An odd number*The smallest number that can't be represented as a sum of fewer than 19 fourth powers*A strictly non-palindromic number...
, 9797 (number)97 is the natural number following 96 and preceding 98.-In mathematics:97 is the 25th prime number , following 89 and preceding 101. 97 is a Proth prime as it is 3 × 25 + 1.The numbers 97, 907, 9007, 90007 and 900007 are happy primes...
, 101101 (number)101 is the natural number following 100 and preceding 102.It is variously pronounced "one hundred and one" / "a hundred and one", "one hundred one" / "a hundred one", and "one oh one"...
, 107107 (number)107 is the natural number following 106 and preceding 108.-In mathematics:One hundred [and] seven is the 28th prime number. The next prime is 109, with which it comprises a twin prime, making 107 a Chen prime....
, 127127 (number)127 is the natural number following 126 and preceding 128.- In mathematics :*As a Mersenne prime, 127 is related to the perfect number 8128. 127 is also an exponent for the Mersenne prime 2127 - 1, making 127 a double Mersenne prime...
, 137137 (number)137 is the natural number following 136 and preceding 138.-In mathematics :One hundred [and] thirty-seven is the 33rd prime number; the next is 139, with which it comprises a twin prime, and thus 137 is a Chen prime. 137 is an Eisenstein prime with no imaginary part and a real part of the form 3n -...
, 149149 (number)149 is the natural number between 148 and 150. It is also a prime number.-In mathematics:*149 is the 35th prime number, and with the next prime number, 151, is a twin prime, thus 149 is a Chen prime. 149 is a strong prime in the sense that it is more than the arithmetic mean of its two neighboring...
, 163163 (number)163 is the natural number following 162 and preceding 164.-In mathematics:163 is a strong prime in the sense that it is greater than the arithmetic mean of its two neighboring primes...
, 179179 (number)179 is the natural number following 178 and preceding 180.-In mathematics:* 179 is an odd number* 179 is a deficient number, as 1 is less than 179* 179 is a Gaussian number* 179 is an odious number* 179 is a square-free number...
, 191191 (number)191 is the natural number following 190 and preceding 192.-In mathematics:* 191 is an odd number* 191 is a centered 19-gonal number* 191 is a deficient number, as 1 is less than 191...
, 197197 (number)197 is the natural number following 196 and preceding 198.-In mathematics:* 197 is an odd number* 197 is a prime number** 197 is a Chen prime** 197 is an Eisenstein prime with no imaginary part** 197 is a strong prime** 197 is a twin prime with 199...
, 223223 (number)223 is the natural number between 222 and 224. It is also a prime number.-In mathematics:223 is a long prime, a strong prime, a lucky prime and a sexy prime .223 is the fourth Carol number and the third to be prime....
, 227, 239, 251, 269, 277, 281, 307, 311, 331, 347, 367, 379, 397, 419, 431, 439, 457, 461, 479, 487, 499 .
For example, 17 is the seventh prime. The sixth and eighth primes, 13 and 19, add up to 32, and half that is 16. That is less than 17, thus 17 is a strong prime.
In a twin prime
Twin prime
A twin prime is a prime number that differs from another prime number by two. Except for the pair , this is the smallest possible difference between two primes. Some examples of twin prime pairs are , , , , and...
pair (p, p + 2) with p > 5, p is always a strong prime, since 3 must divide p − 2 which cannot be prime.
It is possible for a prime to be a strong prime both in the cryptographic sense and the number theoretic sense. For the sake of illustration, 439351292910452432574786963588089477522344331 is a strong prime in the number theoretic sense because the arithmetic mean of its two neighboring primes is 62 less. Without the aid of a computer, this number would be a strong prime in the cryptographic sense because 439351292910452432574786963588089477522344330 has the large prime factor 1747822896920092227343 (and in turn the number one less than that has the large prime factor 1683837087591611009), 439351292910452432574786963588089477522344332 has the large prime factor 864608136454559457049 (and in turn the number one less than that has the large prime factor 105646155480762397). Even using algorithms more advanced than trial by division, these numbers would be difficult to factor by hand. For a modern computer algebra system
Computer algebra system
A computer algebra system is a software program that facilitates symbolic mathematics. The core functionality of a CAS is manipulation of mathematical expressions in symbolic form.-Symbolic manipulations:...
, these numbers can be factored almost instantaneously. A cryptographically strong prime has to be much larger than this example.
Factoring-based cryptosystems
Some people suggest that in the key generationKey generation
Key generation is the process of generating keys for cryptography. A key is used to encrypt and decrypt whatever data is being encrypted/decrypted....
process in RSA cryptosystems, the modulus
should be chosen as the product of two strong primes. This makes the factorization of 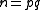using Pollard's p − 1 algorithm computationally infeasible. For this reason, strong primes are required by the ANSI X9.31 standard for use in generating RSA keys for digital signatureDigital signature
A digital signature or digital signature scheme is a mathematical scheme for demonstrating the authenticity of a digital message or document. A valid digital signature gives a recipient reason to believe that the message was created by a known sender, and that it was not altered in transit...
s. However, strong primes do not protect against modulus factorisation using newer algorithms such as Lenstra elliptic curve factorization
Lenstra elliptic curve factorization
The Lenstra elliptic curve factorization or the elliptic curve factorization method is a fast, sub-exponential running time algorithm for integer factorization which employs elliptic curves. For general purpose factoring, ECM is the third-fastest known factoring method...
and Number Field Sieve algorithm. Given the additional cost of generating strong primes RSA Security
RSA Security
RSA, the security division of EMC Corporation, is headquartered in Bedford, Massachusetts, United States, and maintains offices in Australia, Ireland, Israel, the United Kingdom, Singapore, India, China, Hong Kong and Japan....
do not currently recommend their use in key generation
Key generation
Key generation is the process of generating keys for cryptography. A key is used to encrypt and decrypt whatever data is being encrypted/decrypted....
. Similar (and more technical) argument is also given by Rivest and Silverman .
Discrete-logarithm-based cryptosystems
It is shown by Stephen Pohlig and Martin HellmanMartin Hellman
Martin Edward Hellman is an American cryptologist, and is best known for his invention of public key cryptography in cooperation with Whitfield Diffie and Ralph Merkle...
in 1978 that if all the factors of p-1 are less than
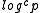, then the problem of solving discrete logarithmDiscrete logarithm
In mathematics, specifically in abstract algebra and its applications, discrete logarithms are group-theoretic analogues of ordinary logarithms. In particular, an ordinary logarithm loga is a solution of the equation ax = b over the real or complex numbers...
modulo p is in P. Therefore, for cryptosystems based on discrete logarithm, such as DSA
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
, it is required that p-1 have at least one large prime factor.
See also
A computationally large safe primeSafe prime
A safe prime is a prime number of the form 2p + 1, where p is also a prime. The first few safe primes are...
is likely to be a cryptographically strong prime.
Note that the criteria for determining if a pseudoprime is a strong pseudoprime
Strong pseudoprime
In number theory, a strong pseudoprime is a composite number that passes a primality test. All primes pass this test, but a small fraction of composites pass as well, making them "false primes"...
is by congruences to powers of a base, not by inequality to the arithmetic mean of neighboring pseudoprimes.
When a prime is equal to the mean of its neighboring primes, it's called a balanced prime. When it's less, it's called a weak prime.