Subgroup growth
Encyclopedia
In mathematics
, subgroup growth is a branch of group theory
, dealing with quantitative questions about subgroup
s of a given group
.
Let G be a finitely generated group. Then, for each integer n define n(G) to be the number of subgroups U of index
n in G. Similarly, if G is a topological group
, s_n(G) denotes the number of open subgroups U of index n in G. One similarly defines 'm_n(G) and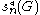
to denote the number of maximal
and normal subgroup
s of index n, respectively.
Subgroup growth studies these functions, their interplay, and the characterization of group theoretical properties in terms of these functions.
The theory was motivated by the desire to enumerate finite groups of given order, and the analogy with Mikhail Gromov's notion of word growth
.
nilpotent group
. Then there exists a composition series
with infinite cyclic
factors, which induces a bijection (not though necessarily a homomorphism
).
such that group multiplication can be expressed by polynomial functions in these coordinates; in particular, the multiplication is definable. Using methods from the model theory
of p-adic integers, F. Grunewald, D. Segal and G. Smith showed that the local zeta function
is a rational function
in p−s'.
As an example, let G be the discrete Heisenberg group. This group has a presentation
with generators
x, y, z and relations
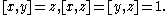
Hence, elements of G can be represented as triples (a, b, c) of integers with group operation given by
To each finite index subgroup
U of G, associate the set of all ``good bases´´ of U as follows. Note that G has a normal series
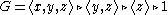
with infinite cyclic
factors
. A triple (g_1, g_2, g_3) in G is called a good basis of U, if g_1, g_2, g_3 generate U, and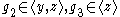
. In general, it is quite complicated to determine the set of good bases for a fixed subgroup U. To overcome this difficulty, one determines the set of all good bases of all finite
index subgroups, and determines how many of these belong to one given subgroup. To make this precise, one has to embed the Heisenberg group over the integers into the group over p-adic number
s. After some computations, one arrives at the formula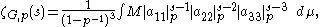
where μ is the Haar measure
on Zp,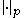
denotes the p-adic absolute value
and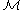
is the set of tuples of p-adic integers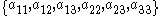
such that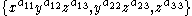
is a good basis of some finite-index subgroup. The latter condition can be translated into
.
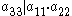Now, the integral can be transformed into an iterated sum to yield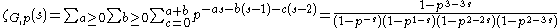
where the final evaluation consists of repeated application of the formula for the value of the geometric series. From this we deduce that ζG(s) can be expressed in terms of the Riemann zeta function as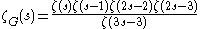
For more complicated examples, the computations become difficult, and in general one cannot expect a closed expression for ζG(s). The local factor
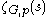
can always be expressed as a definable p-adic integral. Applying a result of MacIntyre
on the model theory of p-adic integers, one deduces again that ζG(s) is a rational function in p−s. Moreover, M. du Sautoy and F. Grunewald showed that the integral can be approximated by Artin L-function
s. Using the fact that Artin L-functions are holomorphic in a neighbourhood of the line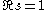
, they showed that for any torsionfree nilpotent group, the function ζG(s) is meromorphic in the domain
where α is the abscissa of convergence of ζG(s), and δ is some positive number, and holomorphic in some neighbourhood of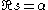
. Using a Tauberian theorem this implies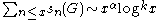
for some real number α and a non-negative integer k.
s of U in G by left shift:
.
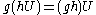In this way, U induces a homomorphism
of G into the symmetric group
on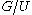
. G acts transitively on 
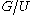, and vice versa, given a transitive action of G on
,
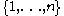the stabilizer of the point 1 is a subgroup of index n in G. Since the set
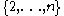
can be permuted in
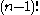
ways, we find that
is equal to the number of transitive G-actions
divided by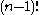
. Among all G-actions, we can distinguish transitive actions by a sifting argument, to arrive at the following formula
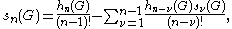
where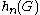
denotes the number of homomorphisms
.
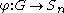In several instances the function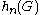
is easier to be approached then 
, and, if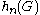 
grows sufficiently large, the sum is of negligible order of magnitude, hence, one obtains an asymptotic
formula for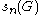
.
As an example, let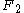
be the free group
on two generators. Then every map of the generators of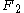
extends to a homomorphism
,
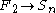that is,
.
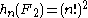From this we deduce
.
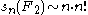For more complicated examples, the estimation of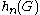
involves the representation theory
and statistical properties of symmetric groups.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, subgroup growth is a branch of group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
, dealing with quantitative questions about subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
s of a given group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
.
Let G be a finitely generated group. Then, for each integer n define n(G) to be the number of subgroups U of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
n in G. Similarly, if G is a topological group
Topological group
In mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
, s_n(G) denotes the number of open subgroups U of index n in G. One similarly defines 'm_n(G) and
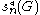to denote the number of maximalMaximal subgroup
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words H is a maximal element of the partially...
and normal subgroup
Normal subgroup
In abstract algebra, a normal subgroup is a subgroup which is invariant under conjugation by members of the group. Normal subgroups can be used to construct quotient groups from a given group....
s of index n, respectively.
Subgroup growth studies these functions, their interplay, and the characterization of group theoretical properties in terms of these functions.
The theory was motivated by the desire to enumerate finite groups of given order, and the analogy with Mikhail Gromov's notion of word growth
Gromov's theorem on groups of polynomial growth
In geometric group theory, Gromov's theorem on groups of polynomial growth, named for Mikhail Gromov, characterizes finitely generated groups of polynomial growth, as those groups which have nilpotent subgroups of finite index....
.
Nilpotent groups
Let G be a finitely generated torsionfreeTorsion subgroup
In the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
nilpotent group
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
. Then there exists a composition series
Composition series
In abstract algebra, a composition series provides a way to break up an algebraic structure, such as a group or a module, into simple pieces. The need for considering composition series in the context of modules arises from the fact that many naturally occurring modules are not semisimple, hence...
with infinite cyclic
Cyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
factors, which induces a bijection (not though necessarily a homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
).
- Zn → G
such that group multiplication can be expressed by polynomial functions in these coordinates; in particular, the multiplication is definable. Using methods from the model theory
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
of p-adic integers, F. Grunewald, D. Segal and G. Smith showed that the local zeta function
is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
in p−s'.
As an example, let G be the discrete Heisenberg group. This group has a presentation
Presentation
Presentation is the practice of showing and explaining the content of a topic to an audience or learner. Presentations come in nearly as many forms as there are life situations...
with generators
Generating set of a group
In abstract algebra, a generating set of a group is a subset that is not contained in any proper subgroup of the group. Equivalently, a generating set of a group is a subset such that every element of the group can be expressed as the combination of finitely many elements of the subset and their...
x, y, z and relations
Presentation of a group
In mathematics, one method of defining a group is by a presentation. One specifies a set S of generators so that every element of the group can be written as a product of powers of some of these generators, and a set R of relations among those generators...
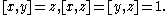
Hence, elements of G can be represented as triples (a, b, c) of integers with group operation given by
To each finite index subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
U of G, associate the set of all ``good bases´´ of U as follows. Note that G has a normal series
Normal series
In mathematics, a subgroup series is a chain of subgroups:1 = A_0 \leq A_1 \leq \cdots \leq A_n = G.Subgroup series can simplify the study of a group to the study of simpler subgroups and their relations, and several subgroup series can be invariantly defined and are important invariants of groups...
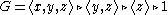
with infinite cyclic
Cyclic number (group theory)
A cyclic number is a natural number n such that n and φ are coprime. Here φ is Euler's totient function. An equivalent definition is that a number n is cyclic iff any group of order n is cyclic.Any prime number is clearly cyclic...
factors
Divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer which divides n without leaving a remainder.-Explanation:...
. A triple (g_1, g_2, g_3) in G is called a good basis of U, if g_1, g_2, g_3 generate U, and
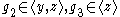. In general, it is quite complicated to determine the set of good bases for a fixed subgroup U. To overcome this difficulty, one determines the set of all good bases of all finiteindex subgroups, and determines how many of these belong to one given subgroup. To make this precise, one has to embed the Heisenberg group over the integers into the group over p-adic number
P-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
s. After some computations, one arrives at the formula
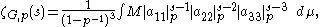
where μ is the Haar measure
Haar measure
In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
on Zp,
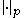denotes the p-adic absolute valueP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
and
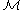is the set of tuples of p-adic integers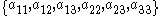such that
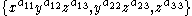
is a good basis of some finite-index subgroup. The latter condition can be translated into
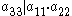.Now, the integral can be transformed into an iterated sum to yield
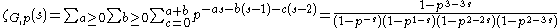
where the final evaluation consists of repeated application of the formula for the value of the geometric series. From this we deduce that ζG(s) can be expressed in terms of the Riemann zeta function as
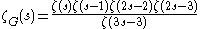
For more complicated examples, the computations become difficult, and in general one cannot expect a closed expression for ζG(s). The local factor
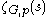
can always be expressed as a definable p-adic integral. Applying a result of MacIntyre
MacIntyre
MacIntyre or Macintyre is a Scottish surname, of Gaelic origin, relating to Clan MacIntyre. Its meaning is "Son of the Carpenter". The anglicized version of the MacIntyre name is Wright....
on the model theory of p-adic integers, one deduces again that ζG(s) is a rational function in p−s. Moreover, M. du Sautoy and F. Grunewald showed that the integral can be approximated by Artin L-function
Artin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s. Using the fact that Artin L-functions are holomorphic in a neighbourhood of the line
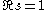, they showed that for any torsionfree nilpotent group, the function ζG(s) is meromorphic in the domain- Re s > α − δ,
where α is the abscissa of convergence of ζG(s), and δ is some positive number, and holomorphic in some neighbourhood of
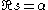. Using a Tauberian theorem this implies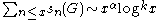for some real number α and a non-negative integer k.
Subgroup growth and coset representations
Let G be a group, U a subgroup of index n. Then G acts on the set of left cosetCoset
In mathematics, if G is a group, and H is a subgroup of G, and g is an element of G, thenA coset is a left or right coset of some subgroup in G...
s of U in G by left shift:
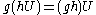.In this way, U induces a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
of G into the symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
on
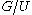. G acts transitively on 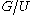, and vice versa, given a transitive action of G on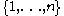,the stabilizer of the point 1 is a subgroup of index n in G. Since the set
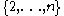
can be permuted in
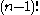
ways, we find that
is equal to the number of transitive G-actionsGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
divided by
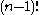. Among all G-actions, we can distinguish transitive actions by a sifting argument, to arrive at the following formula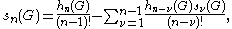where
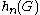denotes the number of homomorphisms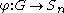.In several instances the function
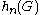is easier to be approached then , and, if 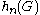grows sufficiently large, the sum is of negligible order of magnitude, hence, one obtains an asymptoticAsymptotic expansion
In mathematics an asymptotic expansion, asymptotic series or Poincaré expansion is a formal series of functions which has the property that truncating the series after a finite number of terms provides an approximation to a given function as the argument of the function tends towards a particular,...
formula for
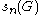.As an example, let
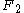be the free groupFree group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
on two generators. Then every map of the generators of
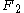extends to a homomorphism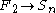,that is,
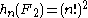.From this we deduce
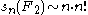.For more complicated examples, the estimation of
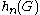involves the representation theoryRepresentation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
and statistical properties of symmetric groups.