
Substitution (algebra)
Encyclopedia
In algebra
, the operation of substitution can be applied in various contexts involving formal objects containing symbols (often called variable
s or indeterminate
s); the operation consists of systematically replacing occurrences of some symbol by a given value.
A common case of substitution involves polynomial
s, where substitution of a numerical value for the indeterminate of a (univariate) polynomial amounts to evaluating the polynomial at that value. Indeed this operation occurs so frequently that the notation for polynomials is often adapted to it; instead of designating a polynomial by a name like P as one would do for other mathematical objects one could define say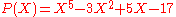
so that substitution for X can be designated by replacement inside "P(X)", say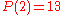 or
or 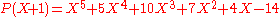 .
.
Substitution can however also applied to other kinds of formal objects built from symbols, for instance elements of free group
s. In order for substitution to be defined, one needs an algebraic structure with an appropriate universal property
, that asserts the existence of unique homomorphisms that send indeterminates to specific values; the substitution then amounts to finding the image under such a homomorphism.
Substitution is related to, but not identical to function composition
; it is also closely related to β-reduction in lambda calculus
. In contrast to these notions however, the accent in algebra is on the preservation of algebraic structure by the substitution operation, the fact that substitution gives a homomorphism
for the structure at hand (in the case of polynomials, the ring
structure).
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
, the operation of substitution can be applied in various contexts involving formal objects containing symbols (often called variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
s or indeterminate
Indeterminate (variable)
In mathematics, and particularly in formal algebra, an indeterminate is a symbol that does not stand for anything else but itself. In particular it does not designate a constant, or a parameter of the problem, it is not an unknown that could be solved for, it is not a variable designating a...
s); the operation consists of systematically replacing occurrences of some symbol by a given value.
A common case of substitution involves polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s, where substitution of a numerical value for the indeterminate of a (univariate) polynomial amounts to evaluating the polynomial at that value. Indeed this operation occurs so frequently that the notation for polynomials is often adapted to it; instead of designating a polynomial by a name like P as one would do for other mathematical objects one could define say
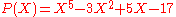
so that substitution for X can be designated by replacement inside "P(X)", say
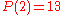 or
or 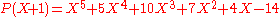 .
.Substitution can however also applied to other kinds of formal objects built from symbols, for instance elements of free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s. In order for substitution to be defined, one needs an algebraic structure with an appropriate universal property
Universal property
In various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
, that asserts the existence of unique homomorphisms that send indeterminates to specific values; the substitution then amounts to finding the image under such a homomorphism.
Substitution is related to, but not identical to function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
; it is also closely related to β-reduction in lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. In contrast to these notions however, the accent in algebra is on the preservation of algebraic structure by the substitution operation, the fact that substitution gives a homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
for the structure at hand (in the case of polynomials, the ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure).

