Supersymmetric quantum mechanics
Encyclopedia
In theoretical physics
, supersymmetric quantum mechanics is an area of research where mathematical concepts from high-energy physics are applied to the seemingly more prosaic field of quantum mechanics
.
as opposed to quantum field theory
. It was hoped that studying SUSY's consequences in this simpler setting would lead to new understanding; remarkably, the effort created new areas of research in quantum mechanics itself.
For example, as of 2004 students are typically taught to "solve" the hydrogen
atom by a laborious process which begins by inserting the Coulomb potential into the Schrödinger equation
. After a considerable amount of work using many differential equations, the analysis produces a recursion relation for the Laguerre polynomials
. The final outcome is the spectrum
of hydrogen-atom energy states (labeled by quantum numbers n and l). Using ideas drawn from SUSY, the final result can be derived with significantly greater ease, in much the same way that operator methods are used to solve the harmonic oscillator
. Oddly enough, this approach is analogous to the way Erwin Schrödinger
first solved the hydrogen atom. Of course, he did not call his solution supersymmetric, as SUSY was thirty years in the future—but it is still remarkable that the SUSY approach, both older and more elegant, is taught in so few universities.
The SUSY solution of the hydrogen atom is only one example of the very general class of solutions which SUSY provides to shape-invariant potentials, a category which includes most potentials taught in introductory quantum mechanics courses.
SUSY quantum mechanics involves pairs of Hamiltonian
s which share a particular mathematical relationship, which are called partner Hamiltonians. (The potential energy
terms which occur in the Hamiltonians are then called partner potentials.) An introductory theorem shows that for every eigenstate of one Hamiltonian, its partner Hamiltonian has a corresponding eigenstate with the same energy (except possibly for zero energy eigenstates). This fact can be exploited to deduce many properties of the eigenstate spectrum. It is analogous to the original description of SUSY, which referred to bosons and fermions. We can imagine a "bosonic Hamiltonian", whose eigenstates are the various bosons of our theory. The SUSY partner of this Hamiltonian would be "fermionic", and its eigenstates would be the theory's fermions. Each boson would have a fermionic partner of equal energy—but, in the relativistic world, energy and mass are interchangeable, so we can just as easily say that the partner particles have equal mass.
SUSY concepts have provided useful extensions to the WKB approximation
. In addition, SUSY has been applied to non-quantum statistical mechanics
through the Fokker-Planck equation
, showing that even if the original inspiration in high-energy particle physics turns out to be a blind alley, its investigation has brought about many useful benefits.
relations among those operators. For example, the canonical operators of position and momentum have the commutator [x,p]=i. (Here, we use "natural units" where Planck's constant is set equal to 1.) A more intricate case is the algebra of angular momentum
operators; these quantities are closely connected to the rotational symmetries of three-dimensional space. To generalize this concept, we define an anticommutator, which relates operators the same way as an ordinary commutator
, but with the opposite sign:
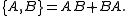
If operators are related by anticommutators as well as commutators, we say they are part of a Lie superalgebra
. Let's say we have a quantum system described by a Hamiltonian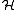
and a set of N self-adjoint operators Qi. We shall call this system supersymmetric if the following anticommutation relation is valid for all 
:
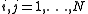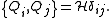
If this is the case, then we call Qi the system's supercharges.
") be an arbitrary complex analytic function of x and define the supersymmetric operators
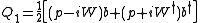
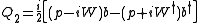
Note that Q1 and Q2 are self-adjoint. Let the Hamiltonian
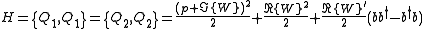
where W' is the derivative of W. Also note that {Q1,Q2}=0. This is nothing other than N = 2 supersymmetry. Note that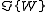 
acts like an electromagnetic vector potential
.
Let's also call the spin down state "bosonic" and the spin up state "fermionic". This is only in analogy to quantum field theory and should not be taken literally. Then, Q1 and Q2 maps "bosonic" states into "fermionic" states and vice versa.
Let's reformulate this a bit:
Define
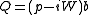
and of course,
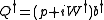
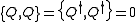
and
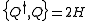
An operator is "bosonic" if it maps "bosonic" states to "bosonic" states and "fermionic" states to "fermionic" states. An operator is "fermionic" if it maps "bosonic" states to "fermionic" states and vice versa. Any operator can be expressed uniquely as the sum of a bosonic operator and a fermionic operator. Define the supercommutator[,} as follows: Between two bosonic operators or a bosonic and a fermionic operator, it is none other than the commutator
but between two fermionic operators, it is an anticommutator.
Then, x and p are bosonic operators and b,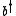
, Q and 
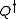are fermionic operators.
Let's work in the Heisenberg picture
where x, b and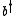
are functions of time.
Then,
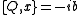
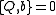
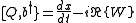
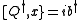
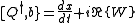
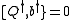
This is nonlinear in general: i.e., x(t), b(t) and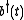
do not form a linear SUSY representation because 
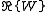isn't necessarily linear in x. To avoid this problem, define the self-adjoint operator 
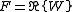. Then,
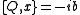
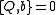
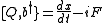
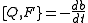
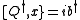
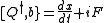
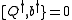
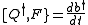
and we see that we have a linear SUSY representation.
Now let's introduce two "formal" quantities,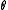
; and 
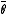with the latter being the adjoint of the former such that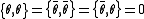
and both of them commute with bosonic operators but anticommute with fermionic ones.
Next, we define a construct called a superfield
:
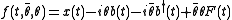
f is self-adjoint, of course. Then,
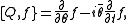
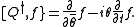
Incidentally, there's also a U(1)R symmetry, with p and x and W having zero R-charges and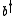
having an R-charge of 1 and b having an R-charge of -1.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
, supersymmetric quantum mechanics is an area of research where mathematical concepts from high-energy physics are applied to the seemingly more prosaic field of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
.
Introduction
Understanding the consequences of supersymmetry has proven mathematically daunting, and it has likewise been difficult to develop theories that could account for symmetry breaking, i.e., the lack of observed partner particles of equal mass. To make progress on these problems, physicists developed supersymmetric quantum mechanics, an application of the supersymmetry (SUSY) superalgebra to quantum mechanicsQuantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as opposed to quantum field theory
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
. It was hoped that studying SUSY's consequences in this simpler setting would lead to new understanding; remarkably, the effort created new areas of research in quantum mechanics itself.
For example, as of 2004 students are typically taught to "solve" the hydrogen
Hydrogen
Hydrogen is the chemical element with atomic number 1. It is represented by the symbol H. With an average atomic weight of , hydrogen is the lightest and most abundant chemical element, constituting roughly 75% of the Universe's chemical elemental mass. Stars in the main sequence are mainly...
atom by a laborious process which begins by inserting the Coulomb potential into the Schrödinger equation
Schrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
. After a considerable amount of work using many differential equations, the analysis produces a recursion relation for the Laguerre polynomials
Laguerre polynomials
In mathematics, the Laguerre polynomials, named after Edmond Laguerre ,are the canonical solutions of Laguerre's equation:x\,y + \,y' + n\,y = 0\,which is a second-order linear differential equation....
. The final outcome is the spectrum
Spectrum (disambiguation)
A spectrum is a condition or value that is not limited to a specific set of values but can vary infinitely within a continuum.Spectrum may also refer to:-Physical science:* Electromagnetic spectrum...
of hydrogen-atom energy states (labeled by quantum numbers n and l). Using ideas drawn from SUSY, the final result can be derived with significantly greater ease, in much the same way that operator methods are used to solve the harmonic oscillator
Harmonic oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
. Oddly enough, this approach is analogous to the way Erwin Schrödinger
Erwin Schrödinger
Erwin Rudolf Josef Alexander Schrödinger was an Austrian physicist and theoretical biologist who was one of the fathers of quantum mechanics, and is famed for a number of important contributions to physics, especially the Schrödinger equation, for which he received the Nobel Prize in Physics in 1933...
first solved the hydrogen atom. Of course, he did not call his solution supersymmetric, as SUSY was thirty years in the future—but it is still remarkable that the SUSY approach, both older and more elegant, is taught in so few universities.
The SUSY solution of the hydrogen atom is only one example of the very general class of solutions which SUSY provides to shape-invariant potentials, a category which includes most potentials taught in introductory quantum mechanics courses.
SUSY quantum mechanics involves pairs of Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
s which share a particular mathematical relationship, which are called partner Hamiltonians. (The potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
terms which occur in the Hamiltonians are then called partner potentials.) An introductory theorem shows that for every eigenstate of one Hamiltonian, its partner Hamiltonian has a corresponding eigenstate with the same energy (except possibly for zero energy eigenstates). This fact can be exploited to deduce many properties of the eigenstate spectrum. It is analogous to the original description of SUSY, which referred to bosons and fermions. We can imagine a "bosonic Hamiltonian", whose eigenstates are the various bosons of our theory. The SUSY partner of this Hamiltonian would be "fermionic", and its eigenstates would be the theory's fermions. Each boson would have a fermionic partner of equal energy—but, in the relativistic world, energy and mass are interchangeable, so we can just as easily say that the partner particles have equal mass.
SUSY concepts have provided useful extensions to the WKB approximation
WKB approximation
In mathematical physics, the WKB approximation or WKB method is a method for finding approximate solutions to linear partial differential equations with spatially varying coefficients...
. In addition, SUSY has been applied to non-quantum statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
through the Fokker-Planck equation
Fokker-Planck equation
The Fokker–Planck equation describes the time evolution of the probability density function of the velocity of a particle, and can be generalized to other observables as well.It is named after Adriaan Fokkerand Max Planck...
, showing that even if the original inspiration in high-energy particle physics turns out to be a blind alley, its investigation has brought about many useful benefits.
The SUSY QM superalgebra
In fundamental quantum mechanics, we learn that an algebra of operators is defined by commutationCommutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
relations among those operators. For example, the canonical operators of position and momentum have the commutator [x,p]=i. (Here, we use "natural units" where Planck's constant is set equal to 1.) A more intricate case is the algebra of angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
operators; these quantities are closely connected to the rotational symmetries of three-dimensional space. To generalize this concept, we define an anticommutator, which relates operators the same way as an ordinary commutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
, but with the opposite sign:
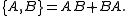
If operators are related by anticommutators as well as commutators, we say they are part of a Lie superalgebra
Lie superalgebra
In mathematics, a Lie superalgebra is a generalisation of a Lie algebra to include a Z2-grading. Lie superalgebras are important in theoretical physics where they are used to describe the mathematics of supersymmetry...
. Let's say we have a quantum system described by a Hamiltonian
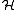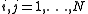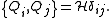
and a set of N self-adjoint operators Qi. We shall call this system supersymmetric if the following anticommutation relation is valid for all :If this is the case, then we call Qi the system's supercharges.
Example
Let's look at the example of a one-dimensional nonrelativistic particle with a 2D (i.e., two states) internal degree of freedom called "spin" (it's not really spin because "real" spin is a property of 3D particles). Let b be an operator which transforms a "spin up" particle into a "spin down" particle. Its adjoint b† then transforms a spin down particle into a spin up particle; the operators are normalized such that the anticommutator {b,b†}=1. And of course, b2=0. Let p be the momentum of the particle and x be its position with [x,p]=i. Let W (the "superpotentialSuperpotential
Superpotential is a concept from particle physics' supersymmetry.-Example of superpotentiality:Let's look at the example of a one dimensional nonrelativistic particle with a 2D internal degree of freedom called "spin"...
") be an arbitrary complex analytic function of x and define the supersymmetric operators
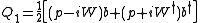
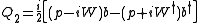
Note that Q1 and Q2 are self-adjoint. Let the Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
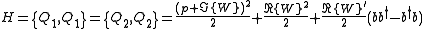
where W
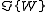acts like an electromagnetic vector potentialVector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
.
Let's also call the spin down state "bosonic" and the spin up state "fermionic". This is only in analogy to quantum field theory and should not be taken literally. Then, Q1 and Q2 maps "bosonic" states into "fermionic" states and vice versa.
Let's reformulate this a bit:
Define
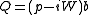
and of course,
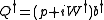
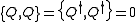
and
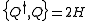
An operator is "bosonic" if it maps "bosonic" states to "bosonic" states and "fermionic" states to "fermionic" states. An operator is "fermionic" if it maps "bosonic" states to "fermionic" states and vice versa. Any operator can be expressed uniquely as the sum of a bosonic operator and a fermionic operator. Define the supercommutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
but between two fermionic operators, it is an anticommutator.
Then, x and p are bosonic operators and b,
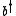, Q and 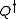are fermionic operators.Let's work in the Heisenberg picture
Heisenberg picture
In physics, the Heisenberg picture is a formulation of quantum mechanics in which the operators incorporate a dependency on time, but the state vectors are time-independent. It stands in contrast to the Schrödinger picture in which the operators are constant and the states evolve in time...
where x, b and
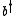are functions of time.Then,
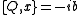
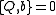
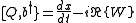
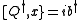
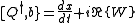
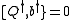
This is nonlinear in general: i.e., x(t), b(t) and
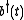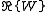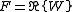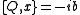
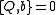
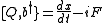
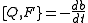
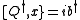
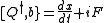
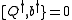
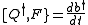
do not form a linear SUSY representation because isn't necessarily linear in x. To avoid this problem, define the self-adjoint operator . Then,and we see that we have a linear SUSY representation.
Now let's introduce two "formal" quantities,
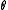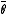; and with the latter being the adjoint of the former such that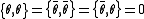and both of them commute with bosonic operators but anticommute with fermionic ones.
Next, we define a construct called a superfield
Superfield
In theoretical physics, one often analyzes theories with supersymmetry in which superfields play a very important role. In four dimensions, the simplest example - namely the minimal N=1 supersymmetry - may be written using a superspace with four extra fermionic coordinates...
:
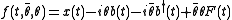
f is self-adjoint, of course. Then,
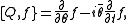
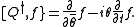
Incidentally, there's also a U(1)R symmetry, with p and x and W having zero R-charges and
having an R-charge of 1 and b having an R-charge of -1.