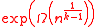Switching lemma
Encyclopedia
In computational complexity theory
, Håstad's switching lemma is a key tool for proving lower bounds on the size of constant-depth Boolean circuits.
Using the switching lemma, showed that Boolean circuits of depth k in which only AND, OR, and NOT gates are allowed require size
for computing the parity function
.
The switching lemma says that depth-2 circuits in which some fraction of the variables have been set randomly depend with high probability only on very few variables after the restriction. The name of the switching lemma stems from the following observation: Take an arbitrary formula in conjunctive normal form
, which is in particular a depth-2 circuit. Now the switching lemma guarantees that after setting some variables randomly, we end up with a Boolean function that depends only on few variables, i.e., it can be computed by a decision tree
of some small depth
. This allows us to write the restricted function as a small formula in disjunctive normal form
. A formula in conjunctive normal form hit by a random restriction of the variables can therefore be "switched" to a small formula in disjunctive normal form.
The original proof of the switching lemma involves an argument with conditional probabilities.
Arguably simpler proofs have been subsequently given by and . For an introduction, see Chapter 14 in .
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, Håstad's switching lemma is a key tool for proving lower bounds on the size of constant-depth Boolean circuits.
Using the switching lemma, showed that Boolean circuits of depth k in which only AND, OR, and NOT gates are allowed require size
for computing the parity function
Parity function
In Boolean algebra, a parity function is a Boolean function whose value is 1 if the input vector has an odd number of ones.The parity function is notable for its role in theoretical investigation of circuit complexity of Boolean functions.-Definition:...
.
The switching lemma says that depth-2 circuits in which some fraction of the variables have been set randomly depend with high probability only on very few variables after the restriction. The name of the switching lemma stems from the following observation: Take an arbitrary formula in conjunctive normal form
Conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form if it is a conjunction of clauses, where a clause is a disjunction of literals.As a normal form, it is useful in automated theorem proving...
, which is in particular a depth-2 circuit. Now the switching lemma guarantees that after setting some variables randomly, we end up with a Boolean function that depends only on few variables, i.e., it can be computed by a decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
of some small depth
. This allows us to write the restricted function as a small formula in disjunctive normal formDisjunctive normal form
In boolean logic, a disjunctive normal form is a standardization of a logical formula which is a disjunction of conjunctive clauses. As a normal form, it is useful in automated theorem proving. A logical formula is considered to be in DNF if and only if it is a disjunction of one or more...
. A formula in conjunctive normal form hit by a random restriction of the variables can therefore be "switched" to a small formula in disjunctive normal form.
The original proof of the switching lemma involves an argument with conditional probabilities.
Arguably simpler proofs have been subsequently given by and . For an introduction, see Chapter 14 in .