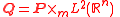Symplectic spinor bundle
Encyclopedia
In differential geometry, given a metaplectic structure
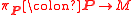 on a
on a 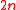 -dimensional symplectic manifold
-dimensional symplectic manifold
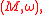 one defines the symplectic spinor bundle to be the Hilbert space
one defines the symplectic spinor bundle to be the Hilbert space
bundle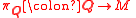 associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group
associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group
—the two-fold covering of the symplectic group
— gives rise to a infinite rank vector bundle
, this is the symplectic spinor construction due to Bertram Kostant
.
A section of the symplectic spinor bundle is called a symplectic spinor field.
is called a symplectic spinor field.
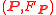 be a metaplectic structure
be a metaplectic structure
on a symplectic manifold
 that is, an equivariant
that is, an equivariant
lift of the symplectic frame bundle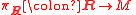 with respect to the double covering
with respect to the double covering 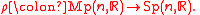
The symplectic spinor bundle is defined to be the Hilbert space bundle
is defined to be the Hilbert space bundle
associated to the metaplectic structure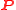 via the metaplectic representation
via the metaplectic representation 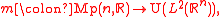 also called the Segal-Shale-Weil representation of
also called the Segal-Shale-Weil representation of 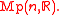 Here, the notation
Here, the notation  denotes the group
denotes the group
of unitary operator
s acting on a Hilbert space

The Segal-Shale-Weil representation is an infinite dimensional unitary representation
of the metaplectic group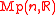 on the space of all complex
on the space of all complex
valued square Lebesgue integrable functions Because of the infinite dimension,
Because of the infinite dimension,
the Segal-Shale-Weil representation is not so easy to handle.
Metaplectic structure
In differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic...
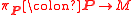 on a
on a 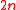 -dimensional symplectic manifold
-dimensional symplectic manifoldSymplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
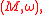 one defines the symplectic spinor bundle to be the Hilbert space
one defines the symplectic spinor bundle to be the Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
bundle
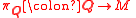 associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic group
associated to the metaplectic structure via the metaplectic representation. The metaplectic representation of the metaplectic groupMetaplectic group
In mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
—the two-fold covering of the symplectic group
Symplectic group
In mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...
— gives rise to a infinite rank vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
, this is the symplectic spinor construction due to Bertram Kostant
Bertram Kostant
-Early life and education:Kostant grew up in New York City, where he graduated from the celebrated Stuyvesant High School in 1945. He went on to obtain an undergraduate degree in mathematics from Purdue University in 1950. He earned his Ph.D...
.
A section of the symplectic spinor bundle
 is called a symplectic spinor field.
is called a symplectic spinor field.Formal definition
Let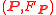 be a metaplectic structure
be a metaplectic structureMetaplectic structure
In differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic...
on a symplectic manifold
Symplectic manifold
In mathematics, a symplectic manifold is a smooth manifold, M, equipped with a closed nondegenerate differential 2-form, ω, called the symplectic form. The study of symplectic manifolds is called symplectic geometry or symplectic topology...
 that is, an equivariant
that is, an equivariantEquivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
lift of the symplectic frame bundle
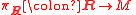 with respect to the double covering
with respect to the double covering 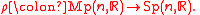
The symplectic spinor bundle
 is defined to be the Hilbert space bundle
is defined to be the Hilbert space bundleBundle (mathematics)
In mathematics, a bundle is a generalization of a fiber bundle dropping the condition of a local product structure. The requirement of a local product structure rests on the bundle having a topology. Without this requirement, more general objects can be considered bundles. For example, one can...
associated to the metaplectic structure
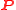 via the metaplectic representation
via the metaplectic representation 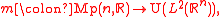 also called the Segal-Shale-Weil representation of
also called the Segal-Shale-Weil representation of 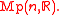 Here, the notation
Here, the notation  denotes the group
denotes the groupGroup (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of unitary operator
Unitary operator
In functional analysis, a branch of mathematics, a unitary operator is a bounded linear operator U : H → H on a Hilbert space H satisfyingU^*U=UU^*=I...
s acting on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...

The Segal-Shale-Weil representation is an infinite dimensional unitary representation
Unitary representation
In mathematics, a unitary representation of a group G is a linear representation π of G on a complex Hilbert space V such that π is a unitary operator for every g ∈ G...
of the metaplectic group
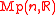 on the space of all complex
on the space of all complexvalued square Lebesgue integrable functions
 Because of the infinite dimension,
Because of the infinite dimension,the Segal-Shale-Weil representation is not so easy to handle.
See also
- Metaplectic groupMetaplectic groupIn mathematics, the metaplectic group Mp2n is a double cover of the symplectic group Sp2n. It can be defined over either real or p-adic numbers...
- Metaplectic structureMetaplectic structureIn differential geometry, a metaplectic structure is the symplectic analog of spin structure on orientable Riemannian manifolds. A metaplectic structure on a symplectic manifold allows one to define the symplectic spinor bundle, which is the Hilbert space bundle associated to the metaplectic...
- Symplectic frame bundle
- Symplectic groupSymplectic groupIn mathematics, the name symplectic group can refer to two different, but closely related, types of mathematical groups, denoted Sp and Sp. The latter is sometimes called the compact symplectic group to distinguish it from the former. Many authors prefer slightly different notations, usually...