T-design
Encyclopedia
In combinatorial
mathematics
, a block design is a set together with a family of subsets
(repeated subsets are allowed at times) whose members are chosen to satisfy some set of properties that are deemed useful for a particular application. These applications come from many areas, including experimental design, finite geometry
, software testing
, cryptography
, and algebraic geometry
. Many variations have been examined, but the most intensely studied are the balanced incomplete block designs (BIBDs or 2-designs) which historically were related to statistical issues in the design of experiments.
"Family" in the above definition can be replaced by "set" if repeated blocks are not allowed. Designs in which repeated blocks are not allowed are called simple.
Here v (the number of elements of X, called points), b (the number of blocks), k, r, and λ are the parameters of the design. (To avoid degenerate examples, it is also assumed that v > k, so that no block contains all the elements of the set. This is the meaning of "incomplete" in the name of these designs.) In a table:
The design is called a (v, k, λ)-design or a (v, b, r, k, λ)-design. The parameters are not all independent; v, k, and λ determine b and r, and not all combinations of v, k, and λ are possible. The two basic equations connecting these parameters are
These conditions are not sufficient as, for example, a (43,7,1)-design does not exist.
The order of a 2-design is defined to be n = r - λ.
A fundamental theorem, Fisher's inequality
, named after Ronald Fisher
, is that b ≥ v in any 2-design. In the case of equality, the 2-design is called a symmetric design
; it has many special features. In a symmetric design r = k holds as well as b = v, and, while it is generally not true in arbitrary 2-designs, in a symmetric design every two distinct blocks meet in λ points.
s (where X is the set of points of the plane and λ = 1), and Steiner triple systems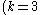
and 
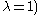. The former is a relatively simple example of a symmetric design. Triple systems 
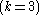are of interest in their own right. Examples of block designs that are not uniform are given by Pairwise block designs (PBD's).
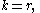
and since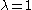
by definition, the second equation gives us
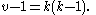
Since k = r we can write the order of a projective plane as n = k - 1 and, from the displayed equation above, we have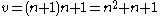
points in a projective plane of order n.
Since a projective plane is symmetric, we have that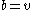
, which means that 
also. The number b is the number of lines of the projective plane. Since λ = 1 there can be no repeated lines, so a projective plane is a simple 2-design in which the number of lines and the number of points are always the same. For a projective plane, k is the number of points on each line and it is equal to n + 1. Similarly, r = n + 1 is the number of lines with which a given point is incident.
For n = 2 we get a projective plane of order 2, also called the Fano plane
, with v = 4 + 2 + 1 = 7 points and 7 lines. In the Fano plane, each line has n + 1 = 3 points and each point belongs to n + 1 = 3 lines.
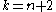points, and has 
points (since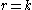 
).
As examples:
where bi is the number of blocks that contain any i-element set of points.
There are no known examples of non-trivial t-(v,k,1)-designs with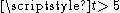
.
The term block design by itself usually means a 2-design.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a block design is a set together with a family of subsets
Family of sets
In set theory and related branches of mathematics, a collection F of subsets of a given set S is called a family of subsets of S, or a family of sets over S. More generally, a collection of any sets whatsoever is called a family of sets...
(repeated subsets are allowed at times) whose members are chosen to satisfy some set of properties that are deemed useful for a particular application. These applications come from many areas, including experimental design, finite geometry
Finite geometry
A finite geometry is any geometric system that has only a finite number of points.Euclidean geometry, for example, is not finite, because a Euclidean line contains infinitely many points, in fact as many points as there are real numbers...
, software testing
Software testing
Software testing is an investigation conducted to provide stakeholders with information about the quality of the product or service under test. Software testing can also provide an objective, independent view of the software to allow the business to appreciate and understand the risks of software...
, cryptography
Cryptography
Cryptography is the practice and study of techniques for secure communication in the presence of third parties...
, and algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
. Many variations have been examined, but the most intensely studied are the balanced incomplete block designs (BIBDs or 2-designs) which historically were related to statistical issues in the design of experiments.
Definition of a BIBD
Given a finite set X (of elements called points) and integers k, r, λ ≥ 1, we define a 2-design (or BIBD, standing for balanced incomplete block design) B to be a family of k-element subsets of X, called blocks, such that the number r of blocks containing x in X is independent of x, and the number λ of blocks containing given distinct points x and y in X is also independent of the choices."Family" in the above definition can be replaced by "set" if repeated blocks are not allowed. Designs in which repeated blocks are not allowed are called simple.
Here v (the number of elements of X, called points), b (the number of blocks), k, r, and λ are the parameters of the design. (To avoid degenerate examples, it is also assumed that v > k, so that no block contains all the elements of the set. This is the meaning of "incomplete" in the name of these designs.) In a table:
| v | points, number of elements of X |
| b | blocks |
| r | number of blocks containing a given point |
| k | number of points in a block |
| λ | number of blocks containing 2 (or more generally t) points |
The design is called a (v, k, λ)-design or a (v, b, r, k, λ)-design. The parameters are not all independent; v, k, and λ determine b and r, and not all combinations of v, k, and λ are possible. The two basic equations connecting these parameters are
These conditions are not sufficient as, for example, a (43,7,1)-design does not exist.
The order of a 2-design is defined to be n = r - λ.
A fundamental theorem, Fisher's inequality
Fisher's inequality
In combinatorial mathematics, Fisher's inequality, named after Ronald Fisher, is a necessary condition for the existence of a balanced incomplete block design satisfying certain prescribed conditions....
, named after Ronald Fisher
Ronald Fisher
Sir Ronald Aylmer Fisher FRS was an English statistician, evolutionary biologist, eugenicist and geneticist. Among other things, Fisher is well known for his contributions to statistics by creating Fisher's exact test and Fisher's equation...
, is that b ≥ v in any 2-design. In the case of equality, the 2-design is called a symmetric design
Symmetric design
In combinatorial mathematics, a symmetric design is a block design with equal numbers of points and blocks. Thus, it has the fewest possible blocks given the number of points . They are also known as projective designs....
; it has many special features. In a symmetric design r = k holds as well as b = v, and, while it is generally not true in arbitrary 2-designs, in a symmetric design every two distinct blocks meet in λ points.
Examples
A block design in which all the blocks have the same size is called uniform. Examples of uniform block designs include finite projective planeProjective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s (where X is the set of points of the plane and λ = 1), and Steiner triple systems
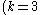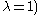and . The former is a relatively simple example of a symmetric design. Triple systems 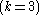are of interest in their own right. Examples of block designs that are not uniform are given by Pairwise block designs (PBD's).Projective planes
Finite projective planes are symmetric 2-designs with λ = 1 and order n > 1. Since these designs are symmetric, it follows from the first basic equation that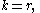and since
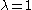by definition, the second equation gives us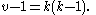Since k = r we can write the order of a projective plane as n = k - 1 and, from the displayed equation above, we have
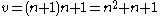points in a projective plane of order n.Since a projective plane is symmetric, we have that
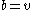, which means that also. The number b is the number of lines of the projective plane. Since λ = 1 there can be no repeated lines, so a projective plane is a simple 2-design in which the number of lines and the number of points are always the same. For a projective plane, k is the number of points on each line and it is equal to n + 1. Similarly, r = n + 1 is the number of lines with which a given point is incident.For n = 2 we get a projective plane of order 2, also called the Fano plane
Fano plane
In finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
, with v = 4 + 2 + 1 = 7 points and 7 lines. In the Fano plane, each line has n + 1 = 3 points and each point belongs to n + 1 = 3 lines.
Biplanes
A biplane or biplane geometry is a symmetric design ("projective" or "square" design), with λ = 2 – any set of two points is contained in two blocks ("lines"), while any two lines intersect in two points. They are similar to finite projective planes, except that rather than two points determining one line (and two lines determining one point), two points determine two lines (respectively, points). A biplane of order n is one whose blocks have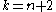 points, and has points (since 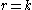).As examples:
- (Trivial) The order 0 biplane has 2 points (and lines of size 2 – (2,2,2)); it is two points, with two blocks, each consisting of both points. Geometrically, it is the digonDigonIn geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
.
- One can also define trivial biplanes of order −1 (1 point, lines of size 1 (2,1,2) – the point is contained in the line) and −2 (1 point, lines of size 0 (2,0,2) – the point is not contained in the line).
- The order 1 biplane has 4 points (and lines of size 3 – (4,3,2)); it is the complete design with v = 4 and k = 3. Geometrically, the points are the vertices and the blocks are the faces of a tetrahedron.
- The order 2 biplane is the complement of the Fano planeFano planeIn finite geometry, the Fano plane is the finite projective plane with the smallest possible number of points and lines: 7 each.-Homogeneous coordinates:...
: it has 7 points (and lines of size 4 – (7,4,2)), where the lines are given as the complements of the (3-point) lines in the Fano plane. - The order 3 biplane has 11 points (and lines of size 5 – (11,5,2)), and is also known as the after Raymond PaleyRaymond PaleyRaymond Edward Alan Christopher Paley was an English mathematician. Paley was born in Bournemouth, England. He was educated at Eton. From there he entered Trinity College, Cambridge where he showed himself the most brilliant student among a remarkable collection of fellow undergraduates...
; it is associated to the Paley digraph of order 11, which is constructed using the field with 11 elements, and is associated to the order 12 Hadamard matrixHadamard matrixIn mathematics, an Hadamard matrix, named after the French mathematician Jacques Hadamard, is a square matrix whose entries are either +1 or −1 and whose rows are mutually orthogonal...
; see Paley construction I.
- Algebraically this corresponds to the exceptional embedding of the projective special linear group
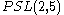in 
– see projective linear group: action on p points for details.
- There are three biplanes of order 4 (16 points, lines of size 6 – (16,6,2)).
- There are five biplanes of order 9 (and 56 points, lines of size 11 – (56,11,2)).
Generalization: t-designs
Given any integer t ≥ 2, a t-design B is a class of k-element subsets of X, called blocks, such that every point x in X appears in exactly r blocks, and every t-element subset T appears in exactly λ blocks. The numbers v (the number of elements of X), b (the number of blocks), k, r, λ, and t are the parameters of the design. The design may be called a t-(v,k,λ)-design. Again, these four numbers determine b and r and the four numbers themselves cannot be chosen arbitrarily. The equations arewhere bi is the number of blocks that contain any i-element set of points.
There are no known examples of non-trivial t-(v,k,1)-designs with
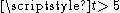.The term block design by itself usually means a 2-design.
External links
- Design DB: A database of combinatorial, statistical, experimental block designs