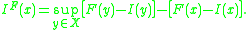Tilted large deviation principle
Encyclopedia
In mathematics
— specifically, in large deviations theory
— the tilted large deviation principle is a result that allows one to generate a new large deviation principle
from an old one by "tilting", i.e. integration
against an exponential
functional
. It can be seen as an alternative formulation of Varadhan's lemma
.
(i.e., a separable, completely metrizable topological space
), and let (με)ε>0 be a family of probability measures
on X that satisfies the large deviation principle with rate function
I : X → [0, +∞]. Let F : X → R be a continuous function
that is bounded
from above. For each Borel set S ⊆ X, let
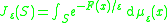
and define a new family of probability measures (νε)ε>0 on X by
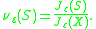
Then (νε)ε>0 satisfies the large deviation principle on X with rate function IF : X → [0, +∞] given by
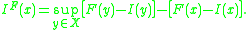
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
— specifically, in large deviations theory
Large deviations theory
In probability theory, the theory of large deviations concerns the asymptotic behaviour of remote tails of sequences of probability distributions. Some basic ideas of the theory can be tracked back to Laplace and Cramér, although a clear unified formal definition was introduced in 1966 by Varadhan...
— the tilted large deviation principle is a result that allows one to generate a new large deviation principle
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
from an old one by "tilting", i.e. integration
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
against an exponential
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
functional
Functional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
. It can be seen as an alternative formulation of Varadhan's lemma
Varadhan's lemma
In mathematics, Varadhan's lemma is a result in large deviations theory named after S. R. Srinivasa Varadhan. The result gives information on the asymptotic distribution of a statistic φ of a family of random variables Zε as ε becomes small in terms of a rate function for the variables.-Statement...
.
Statement of the theorem
Let X be a Polish spacePolish space
In the mathematical discipline of general topology, a Polish space is a separable completely metrizable topological space; that is, a space homeomorphic to a complete metric space that has a countable dense subset. Polish spaces are so named because they were first extensively studied by Polish...
(i.e., a separable, completely metrizable topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
), and let (με)ε>0 be a family of probability measures
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
on X that satisfies the large deviation principle with rate function
Rate function
In mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
I : X → [0, +∞]. Let F : X → R be a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
that is bounded
Bounded function
In mathematics, a function f defined on some set X with real or complex values is called bounded, if the set of its values is bounded. In other words, there exists a real number M...
from above. For each Borel set S ⊆ X, let
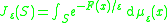
and define a new family of probability measures (νε)ε>0 on X by
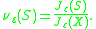
Then (νε)ε>0 satisfies the large deviation principle on X with rate function IF : X → [0, +∞] given by