
Trajectory (fluid mechanics)
Encyclopedia
In fluid mechanics
, meteorology
and oceanography
, a trajectory traces the motion of a single point, often called a parcel, in the flow.
Trajectories are useful for tracking atmospheric contaminants, such as smoke plumes,
and as constituents to Lagrangian simulations,
such as contour advection
or semi-Lagrangian scheme
s.
Suppose we have a time-varying flow field,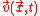 .
.
The motion of a fluid parcel, or trajectory, is given by the following
system of ordinary differential equations:

While the equation looks simple, there are at least three concerns
when attempting to solve it numerically. The first is the
integration scheme
.
This is typically a Runge-Kutta, although others can be useful as
well, such as a leapfrog
. The second is the
method of determining the velocity vector,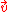
at a given position, , and time, t.
, and time, t.
Normally, it is not known at all positions and times, therefore
some method of interpolation
is required. If the velocities
are gridded in space and time, then bilinear
,
trilinear
or higher dimensional linear
interpolation is appropriate.
Bicubic
, tricubic
, etc.,
interpolation is used as well, but is probably not worth the extra computational
overhead.
Velocity fields can be determined by measurement, e.g. from
weather balloons, from numerical models or especially from a combination
of the two, e.g. assimilation models
.
The final concern is metric corrections. These are necessary for geophysical
fluid flows on a spherical Earth. The differential equations for tracing
a two-dimensional, atmospheric trajectory in longitude-latitude
coordinates are as follows:
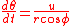
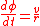
where, and
and  are, respectively,
are, respectively,
the longitude and latitude in radians, r is the radius of the Earth,
u is the zonal wind and v is the meridional wind.
Trajectories can be validated by balloons in the atmosphere
and buoys in the
ocean
.
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, meteorology
Meteorology
Meteorology is the interdisciplinary scientific study of the atmosphere. Studies in the field stretch back millennia, though significant progress in meteorology did not occur until the 18th century. The 19th century saw breakthroughs occur after observing networks developed across several countries...
and oceanography
Oceanography
Oceanography , also called oceanology or marine science, is the branch of Earth science that studies the ocean...
, a trajectory traces the motion of a single point, often called a parcel, in the flow.
Trajectories are useful for tracking atmospheric contaminants, such as smoke plumes,
and as constituents to Lagrangian simulations,
such as contour advection
Contour advection
Contour advection is a Lagrangian methodof simulating the evolution of one or more contours or isolines ofa tracer as it is stirred by a moving fluid....
or semi-Lagrangian scheme
Semi-Lagrangian scheme
The Semi-Lagrangian scheme is a numerical method that is widely used in Numerical Weather Prediction models for the integration of the equations governing atmospheric motion...
s.
Suppose we have a time-varying flow field,
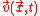 .
.The motion of a fluid parcel, or trajectory, is given by the following
system of ordinary differential equations:

While the equation looks simple, there are at least three concerns
when attempting to solve it numerically. The first is the
integration scheme
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
.
This is typically a Runge-Kutta, although others can be useful as
well, such as a leapfrog
Leapfrog integration
Leapfrog integration is a simple method for numerically integrating differential equations of the form\ddot x=F,or equivalently of the form\dot v=F,\;\dot x \equiv v,particularly in the case of a dynamical system of classical mechanics...
. The second is the
method of determining the velocity vector,
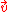
at a given position,
 , and time, t.
, and time, t.Normally, it is not known at all positions and times, therefore
some method of interpolation
Interpolation
In the mathematical field of numerical analysis, interpolation is a method of constructing new data points within the range of a discrete set of known data points....
is required. If the velocities
are gridded in space and time, then bilinear
Bilinear interpolation
In mathematics, bilinear interpolation is an extension of linear interpolation for interpolating functions of two variables on a regular grid. The interpolated function should not use the term of x^2 or y^2, but x y, which is the bilinear form of x and y.The key idea is to perform linear...
,
trilinear
Trilinear interpolation
Trilinear interpolation is a method of multivariate interpolation on a 3-dimensional regular grid. It approximates the value of an intermediate point within the local axial rectangular prism linearly, using data on the lattice points...
or higher dimensional linear
interpolation is appropriate.
Bicubic
Bicubic interpolation
In mathematics, bicubic interpolation is an extension of cubic interpolation for interpolating data points on a two dimensional regular grid. The interpolated surface is smoother than corresponding surfaces obtained by bilinear interpolation or nearest-neighbor interpolation...
, tricubic
Tricubic interpolation
In the mathematical subfield numerical analysis, tricubic interpolation is a method for obtaining values at arbitrary points in 3D space of a function defined on a regular grid...
, etc.,
interpolation is used as well, but is probably not worth the extra computational
overhead.
Velocity fields can be determined by measurement, e.g. from
weather balloons, from numerical models or especially from a combination
of the two, e.g. assimilation models
Data assimilation
Applications of data assimilation arise in many fields of geosciences, perhaps most importantly in weather forecasting and hydrology. Data assimilation proceeds by analysis cycles...
.
The final concern is metric corrections. These are necessary for geophysical
fluid flows on a spherical Earth. The differential equations for tracing
a two-dimensional, atmospheric trajectory in longitude-latitude
coordinates are as follows:
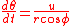
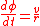
where,
 and
and  are, respectively,
are, respectively,the longitude and latitude in radians, r is the radius of the Earth,
u is the zonal wind and v is the meridional wind.
Trajectories can be validated by balloons in the atmosphere
Atmosphere
An atmosphere is a layer of gases that may surround a material body of sufficient mass, and that is held in place by the gravity of the body. An atmosphere may be retained for a longer duration, if the gravity is high and the atmosphere's temperature is low...
and buoys in the
ocean
Ocean
An ocean is a major body of saline water, and a principal component of the hydrosphere. Approximately 71% of the Earth's surface is covered by ocean, a continuous body of water that is customarily divided into several principal oceans and smaller seas.More than half of this area is over 3,000...
.

