Transfer-matrix method
Encyclopedia
In physics
and mathematics
, the transfer-matrix method is a general technique for solving problems in statistical mechanics.
The basic idea is to write the partition function
in the form
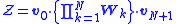
where v0 and vN are vectors of dimension p and the pxp matrices Wk are the so-called transfer matrices. In some cases, particularly for cyclic systems, the partition function may be written more simply as
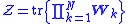
where "tr" denotes the matrix trace
. In either case, the partition function may be solved exactly using eigenanalysis. If the matrices are all the same matrix W, the partition function may be approximated as the N power of the largest eigenvalue of W, since the trace is the sum of the eigenvalues and the eigenvalues of the product of two diagonal matrices equals the product of their individual eigenvalues.
The transfer-matrix method is used when the total system can be broken into a sequence of subsystems that interact only with adjacent subsystems. For example, a three-dimensional cubical lattice of spins
in an Ising model
can be decomposed into a sequence of two-dimensional planar lattices of spins that interact only adjacently. The dimension p of the pxp transfer matrix equals the number of states the subsystem may have; the transfer matrix itself Wk encodes the statistical weight
associated with a particular state of subsystem k-1 being next to another state of subsystem k.
As an example of observables that can be calculated from this method, the probability of a particular state
occurring at position x is given by:
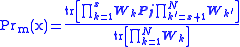
Where
is the projection matrix for state 
, having elements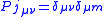 
Transfer-matrix methods have been critical for many exact solutions of problems in statistical mechanics
, including the Zimm-Bragg
and Lifson-Roig model
s of the helix-coil transition
, as well as the famous exact solution of the two-dimensional Ising model
solution by Lars Onsager
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the transfer-matrix method is a general technique for solving problems in statistical mechanics.
The basic idea is to write the partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
in the form
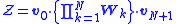
where v0 and vN are vectors of dimension p and the pxp matrices Wk are the so-called transfer matrices. In some cases, particularly for cyclic systems, the partition function may be written more simply as
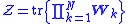
where "tr" denotes the matrix trace
Trace (linear algebra)
In linear algebra, the trace of an n-by-n square matrix A is defined to be the sum of the elements on the main diagonal of A, i.e.,...
. In either case, the partition function may be solved exactly using eigenanalysis. If the matrices are all the same matrix W, the partition function may be approximated as the N power of the largest eigenvalue of W, since the trace is the sum of the eigenvalues and the eigenvalues of the product of two diagonal matrices equals the product of their individual eigenvalues.
The transfer-matrix method is used when the total system can be broken into a sequence of subsystems that interact only with adjacent subsystems. For example, a three-dimensional cubical lattice of spins
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
in an Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
can be decomposed into a sequence of two-dimensional planar lattices of spins that interact only adjacently. The dimension p of the pxp transfer matrix equals the number of states the subsystem may have; the transfer matrix itself Wk encodes the statistical weight
Statistical weight
In statistical mechanics, the statistical weight is the relative probability of a particular feature of a state. If the energy associated with the feature is ΔE, the statistical weight is given by the Boltzmann factor e-ΔE/kT, where k is the Boltzmann constant and T is the temperature in...
associated with a particular state of subsystem k-1 being next to another state of subsystem k.
As an example of observables that can be calculated from this method, the probability of a particular state
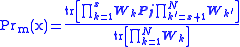
occurring at position x is given by:Where
is the projection matrix for state , having elements 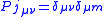Transfer-matrix methods have been critical for many exact solutions of problems in statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, including the Zimm-Bragg
Zimm-Bragg model
In statistical mechanics, the Zimm–Bragg model is a helix-coil transition model that describes helix-coil transitions of macromolecules, usually polymer chains...
and Lifson-Roig model
Lifson-Roig model
In polymer science, the Lifson-Roig model is a helix-coil transition model applied to the alpha helix-random coil transition of polypeptides; it is a refinement of the Zimm-Bragg model that recognizes that a polypeptide alpha helix is only stabilized by a hydrogen bond only once three consecutive...
s of the helix-coil transition
Helix-coil transition model
Helix–coil transition models are formalized techniques in statistical mechanics developed to describe conformations of linear polymers in solution. The models are usually but not exclusively applied to polypeptides as a measure of the relative fraction of the molecule in an alpha helix conformation...
, as well as the famous exact solution of the two-dimensional Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
solution by Lars Onsager
Lars Onsager
Lars Onsager was a Norwegian-born American physical chemist and theoretical physicist, winner of the 1968 Nobel Prize in Chemistry.He held the Gibbs Professorship of Theoretical Chemistry at Yale University....
.