Lifson-Roig model
Encyclopedia
In polymer science
, the Lifson-Roig model is a helix-coil transition model
applied to the alpha helix
-random coil
transition of polypeptides; it is a refinement of the Zimm-Bragg model
that recognizes that a polypeptide alpha helix
is only stabilized by a hydrogen bond
only once three consecutive residues have adopted the helical conformation. To consider three consecutive residues each with two states (helix and coil), the Lifson-Roig model uses a 4x4 transfer matrix instead of the 2x2 transfer matrix of the Zimm-Bragg model, which considers only two consecutive residues. However, the simple nature of the coil state allows this to be reduced to a 3x3 matrix for most applications.
The Zimm-Bragg and Lifson-Roig models are but the first two in a series of analogous transfer-matrix methods in polymer science that have also been applied to nucleic acid
s and branched polymers. The transfer-matrix approach is especially elegant for homopolymers, since the statistical mechanics may be solved exactly using a simple eigenanalysis.
for nucleating
a helix, the weight for propagating a helix and the weight for forming a hydrogen bond, which is granted only if three consecutive residues are in a helical state. Weights are assigned at each position in a polymer as a function of the conformation of the residue in that position and as a function of its two neighbors. A statistical weight of 1 is assigned to the "reference state" of a coil unit whose neighbors are both coils, and a "nucleation" unit is defined (somewhat arbitrarily) as two consecutive helical units neighbored by a coil. A major modification of the original Lifson-Roig model introduces "capping" parameters for the helical termini, in which the N- and C-terminal capping weights may vary independently. The correlation matrix for this modification can be represented as a matrix M, reflecting the statistical weights of the helix state h and coil state c.
The Lifson-Roig model may be solved by the transfer-matrix method
using the transfer matrix M shown at the right, where w is the statistical weight
for helix propagation, v for initiation, n for N-terminal capping, and c for C-terminal capping. (In the traditional model n and c are equal to 1.) The partition function
for the helix-coil transition equilibrium is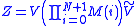
where V is the end vector
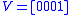, arranged to ensure the coil state of the first and last residues in the polymer.
This strategy for parameterizing helix-coil transitions was originally developed for alpha helices
, whose hydrogen bond
s occur between residues i and i+4; however, it is straightforward to extend the model to 310 helices and pi helices
, with i+3 and i+5 hydrogen bonding patterns respectively. The complete alpha/310/pi transfer matrix includes weights for transitions between helix types as well as between helix and coil states. However, because 310 helices are much more common in the tertiary structure
s of proteins than pi helices, extension of the Lifson-Roig model to accommodate 310 helices - resulting in a 9x9 transfer matrix when capping is included - has found a greater range of application. Analogous extensions of the Zimm-Bragg model have been put forth but have not accommodated mixed helical conformations.
Polymer science
Polymer science or macromolecular science is the subfield of materials science concerned with polymers, primarily synthetic polymers such as plastics...
, the Lifson-Roig model is a helix-coil transition model
Helix-coil transition model
Helix–coil transition models are formalized techniques in statistical mechanics developed to describe conformations of linear polymers in solution. The models are usually but not exclusively applied to polypeptides as a measure of the relative fraction of the molecule in an alpha helix conformation...
applied to the alpha helix
Alpha helix
A common motif in the secondary structure of proteins, the alpha helix is a right-handed coiled or spiral conformation, in which every backbone N-H group donates a hydrogen bond to the backbone C=O group of the amino acid four residues earlier...
-random coil
Random coil
A random coil is a polymer conformation where the monomer subunits are oriented randomly while still being bonded to adjacent units. It is not one specific shape, but a statistical distribution of shapes for all the chains in a population of macromolecules...
transition of polypeptides; it is a refinement of the Zimm-Bragg model
Zimm-Bragg model
In statistical mechanics, the Zimm–Bragg model is a helix-coil transition model that describes helix-coil transitions of macromolecules, usually polymer chains...
that recognizes that a polypeptide alpha helix
Alpha helix
A common motif in the secondary structure of proteins, the alpha helix is a right-handed coiled or spiral conformation, in which every backbone N-H group donates a hydrogen bond to the backbone C=O group of the amino acid four residues earlier...
is only stabilized by a hydrogen bond
Hydrogen bond
A hydrogen bond is the attractive interaction of a hydrogen atom with an electronegative atom, such as nitrogen, oxygen or fluorine, that comes from another molecule or chemical group. The hydrogen must be covalently bonded to another electronegative atom to create the bond...
only once three consecutive residues have adopted the helical conformation. To consider three consecutive residues each with two states (helix and coil), the Lifson-Roig model uses a 4x4 transfer matrix instead of the 2x2 transfer matrix of the Zimm-Bragg model, which considers only two consecutive residues. However, the simple nature of the coil state allows this to be reduced to a 3x3 matrix for most applications.
The Zimm-Bragg and Lifson-Roig models are but the first two in a series of analogous transfer-matrix methods in polymer science that have also been applied to nucleic acid
Nucleic acid
Nucleic acids are biological molecules essential for life, and include DNA and RNA . Together with proteins, nucleic acids make up the most important macromolecules; each is found in abundance in all living things, where they function in encoding, transmitting and expressing genetic information...
s and branched polymers. The transfer-matrix approach is especially elegant for homopolymers, since the statistical mechanics may be solved exactly using a simple eigenanalysis.
Parameterization
The Lifson-Roig model is characterized by three parameters: the statistical weightStatistical weight
In statistical mechanics, the statistical weight is the relative probability of a particular feature of a state. If the energy associated with the feature is ΔE, the statistical weight is given by the Boltzmann factor e-ΔE/kT, where k is the Boltzmann constant and T is the temperature in...
for nucleating
Nucleation
Nucleation is the extremely localized budding of a distinct thermodynamic phase. Some examples of phases that may form by way of nucleation in liquids are gaseous bubbles, crystals or glassy regions. Creation of liquid droplets in saturated vapor is also characterized by nucleation...
a helix, the weight for propagating a helix and the weight for forming a hydrogen bond, which is granted only if three consecutive residues are in a helical state. Weights are assigned at each position in a polymer as a function of the conformation of the residue in that position and as a function of its two neighbors. A statistical weight of 1 is assigned to the "reference state" of a coil unit whose neighbors are both coils, and a "nucleation" unit is defined (somewhat arbitrarily) as two consecutive helical units neighbored by a coil. A major modification of the original Lifson-Roig model introduces "capping" parameters for the helical termini, in which the N- and C-terminal capping weights may vary independently. The correlation matrix for this modification can be represented as a matrix M, reflecting the statistical weights of the helix state h and coil state c.
| M | hh | hc | ch | cc |
|---|---|---|---|---|
| hh | w | v | 0 | 0 |
| hc | 0 | 0 |  |
c |
| ch | v | v | 0 | 0 |
| cc | 0 | 0 | n | 1 |
The Lifson-Roig model may be solved by the transfer-matrix method
Transfer-matrix method
In physics and mathematics, the transfer-matrix method is a general technique for solving problems in statistical mechanics.The basic idea is to write the partition function in the form...
using the transfer matrix M shown at the right, where w is the statistical weight
Statistical weight
In statistical mechanics, the statistical weight is the relative probability of a particular feature of a state. If the energy associated with the feature is ΔE, the statistical weight is given by the Boltzmann factor e-ΔE/kT, where k is the Boltzmann constant and T is the temperature in...
for helix propagation, v for initiation, n for N-terminal capping, and c for C-terminal capping. (In the traditional model n and c are equal to 1.) The partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
for the helix-coil transition equilibrium is
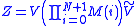
where V is the end vector
Coordinate vector
In linear algebra, a coordinate vector is an explicit representation of a vector in an abstract vector space as an ordered list of numbers or, equivalently, as an element of the coordinate space Fn....
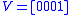, arranged to ensure the coil state of the first and last residues in the polymer.This strategy for parameterizing helix-coil transitions was originally developed for alpha helices
Alpha helix
A common motif in the secondary structure of proteins, the alpha helix is a right-handed coiled or spiral conformation, in which every backbone N-H group donates a hydrogen bond to the backbone C=O group of the amino acid four residues earlier...
, whose hydrogen bond
Hydrogen bond
A hydrogen bond is the attractive interaction of a hydrogen atom with an electronegative atom, such as nitrogen, oxygen or fluorine, that comes from another molecule or chemical group. The hydrogen must be covalently bonded to another electronegative atom to create the bond...
s occur between residues i and i+4; however, it is straightforward to extend the model to 310 helices and pi helices
Pi helix
A pi helix is a type of secondary structure found in proteins. Although thought to be rare, π-helices are actually found in 15% of known protein structures and are believed to be an evolutionary adaptation derived by the insertion of a single amino acid into an α-helix...
, with i+3 and i+5 hydrogen bonding patterns respectively. The complete alpha/310/pi transfer matrix includes weights for transitions between helix types as well as between helix and coil states. However, because 310 helices are much more common in the tertiary structure
Tertiary structure
In biochemistry and molecular biology, the tertiary structure of a protein or any other macromolecule is its three-dimensional structure, as defined by the atomic coordinates.-Relationship to primary structure:...
s of proteins than pi helices, extension of the Lifson-Roig model to accommodate 310 helices - resulting in a 9x9 transfer matrix when capping is included - has found a greater range of application. Analogous extensions of the Zimm-Bragg model have been put forth but have not accommodated mixed helical conformations.