
Turán's theorem
Encyclopedia
In graph theory
, Turán's theorem is a result on the number of edges in a Kr+1
-free graph
.
An n-vertex
graph that does not contain any (r + 1)-vertex clique
may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they belong to two different parts. We call the resulting graph the Turán graph
T(n,r). Turán's theorem states that the Turán graph has the largest number of edges among all Kr+1-free n-vertex graphs.
Turán graph
s were first described and studied by Hungarian
mathematician
Paul Turán in 1941, though a special case of the theorem was stated earlier by Mantel in 1907.
Let G be any subgraph of Kn such that G is Kr+1 -free. Then the number of edges in G is at most
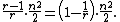
An equivalent formulation is the following:
Among the n-vertex simple graphs with no (r + 1)-cliques, T(n,r) has the maximum number of edges.
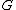 be an n-vertex simple graph with no (r + 1)-clique and with the maximum number of edges.
be an n-vertex simple graph with no (r + 1)-clique and with the maximum number of edges.
The first claim is that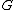 must be a complete r-partite graph (although it's stated more technically below). In other words, we can partition the vertex set into
must be a complete r-partite graph (although it's stated more technically below). In other words, we can partition the vertex set into  subsets
subsets 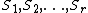 such that if two vertices are in different sets,
such that if two vertices are in different sets, 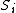 and
and  , then they have an edge between them, but if they are in the same set, then they have no edge between them. The second claim is that the sizes of these sets
, then they have an edge between them, but if they are in the same set, then they have no edge between them. The second claim is that the sizes of these sets 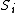 differ from each other by at most 1. For example, if we want the graph on 23 vertices with the most edges that does not contain a triangle, then we partition the vertices into sets
differ from each other by at most 1. For example, if we want the graph on 23 vertices with the most edges that does not contain a triangle, then we partition the vertices into sets 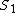 and
and 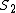 , with
, with 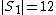 and
and 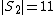 . We add all the edges between the two sets, so the graph will have 11*12 = 132 edges. This matches with the theorem, which says that G will have at most
. We add all the edges between the two sets, so the graph will have 11*12 = 132 edges. This matches with the theorem, which says that G will have at most 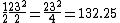 edges.
edges.
(This claim is equivalent to the relation x~y iff x not connected to y
being an equivalence relation. ~ is always
reflexive and symmetric, but only in special cases is it transitive. ~ is not transitive precisely when we have u, v and w with u ~ w and w ~ v without u ~ v.)
Assume the claim is false. Construct a new n-vertex simple graph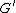 that contains no (r + 1)-clique but has more edges than
that contains no (r + 1)-clique but has more edges than 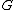 , as follows:
, as follows:
Case 1: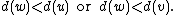
Assume that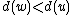 . Delete vertex
. Delete vertex 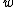 and create a copy of vertex
and create a copy of vertex  (with all of the same neighbors as
(with all of the same neighbors as  ); call it
); call it 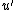 .
.
Any clique in the new graph contains at most one vertex among .
.
So this new graph does not contain any (r + 1)-clique. However, it contains more edges:
Case 2: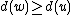 and
and 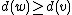
Delete vertices and
and  and create two new copies of vertex
and create two new copies of vertex 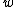 .
.
Again, the new graph does not contain any (r + 1)-clique. However it contains more edges: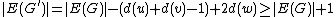 .
.
This proves Claim 1.
The claim proves that one can partition the vertices of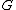 into equivalence classes based on their nonneighbors; i.e. two vertices are in the same equivalence class if they are nonadjacent. This implies that
into equivalence classes based on their nonneighbors; i.e. two vertices are in the same equivalence class if they are nonadjacent. This implies that 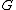
is a complete multipartite graph (where the parts are the equivalence classes).
If G is a complete k-partite graph with parts A and B and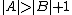 , then we can increase the number of edges in G by moving a vertex from part A to part B. By moving a vertex from part A to part B,
, then we can increase the number of edges in G by moving a vertex from part A to part B. By moving a vertex from part A to part B,
the graph loses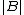 edges, but gains
edges, but gains 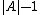 edges. Thus, it gains at least
edges. Thus, it gains at least  edge.
edge.
This proves Claim 2.
This proof shows that the Turan graph has the maximum number of edges.
Additionally, the proof shows that the Turan graph is the only graph that has the maximum number of edges.
The maximum number of edges in an n-vertex triangle-free graph
is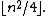
In other words, one must delete nearly half of the edges in Kn to obtain a triangle-free graph.
A strengthened form of Mantel's theorem states that any graph with at least n2/4 edges must either be the complete bipartite graph
Kn/2,n/2 or it must be pancyclic
: not only does it contain a triangle, it must also contain cycles of all other possible lengths up to the number of vertices in the graph .
Another strengthening of Mantel's theorem states that the edges of any graph may be covered by at most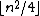 cliques
cliques
: that is, the intersection number
is at most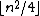 .
.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, Turán's theorem is a result on the number of edges in a Kr+1
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
-free graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
.
An n-vertex
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
graph that does not contain any (r + 1)-vertex clique
Clique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
may be formed by partitioning the set of vertices into r parts of equal or nearly-equal size, and connecting two vertices by an edge whenever they belong to two different parts. We call the resulting graph the Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
T(n,r). Turán's theorem states that the Turán graph has the largest number of edges among all Kr+1-free n-vertex graphs.
Turán graph
Turán graph
The Turán graph T is a graph formed by partitioning a set of n vertices into r subsets, with sizes as equal as possible, and connecting two vertices by an edge whenever they belong to different subsets. The graph will have subsets of size \lceil n/r\rceil, and r- subsets of size \lfloor n/r\rfloor...
s were first described and studied by Hungarian
Hungary
Hungary , officially the Republic of Hungary , is a landlocked country in Central Europe. It is situated in the Carpathian Basin and is bordered by Slovakia to the north, Ukraine and Romania to the east, Serbia and Croatia to the south, Slovenia to the southwest and Austria to the west. The...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Paul Turán in 1941, though a special case of the theorem was stated earlier by Mantel in 1907.
Formal statement
Formally, Turán's theorem may be stated as follows.Let G be any subgraph of Kn such that G is Kr+1 -free. Then the number of edges in G is at most
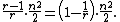
An equivalent formulation is the following:
Among the n-vertex simple graphs with no (r + 1)-cliques, T(n,r) has the maximum number of edges.
Proof
Let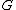 be an n-vertex simple graph with no (r + 1)-clique and with the maximum number of edges.
be an n-vertex simple graph with no (r + 1)-clique and with the maximum number of edges.- Overview: The proof consists of two claims about
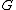 , which we outline, before proving.
, which we outline, before proving.
The first claim is that
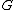 must be a complete r-partite graph (although it's stated more technically below). In other words, we can partition the vertex set into
must be a complete r-partite graph (although it's stated more technically below). In other words, we can partition the vertex set into  subsets
subsets 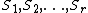 such that if two vertices are in different sets,
such that if two vertices are in different sets, 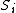 and
and  , then they have an edge between them, but if they are in the same set, then they have no edge between them. The second claim is that the sizes of these sets
, then they have an edge between them, but if they are in the same set, then they have no edge between them. The second claim is that the sizes of these sets 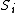 differ from each other by at most 1. For example, if we want the graph on 23 vertices with the most edges that does not contain a triangle, then we partition the vertices into sets
differ from each other by at most 1. For example, if we want the graph on 23 vertices with the most edges that does not contain a triangle, then we partition the vertices into sets 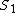 and
and 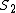 , with
, with 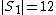 and
and 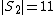 . We add all the edges between the two sets, so the graph will have 11*12 = 132 edges. This matches with the theorem, which says that G will have at most
. We add all the edges between the two sets, so the graph will have 11*12 = 132 edges. This matches with the theorem, which says that G will have at most 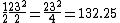 edges.
edges.- Claim 1: Graph
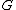 does not contain any three vertices
does not contain any three vertices  such that
such that 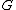 contains edge
contains edge 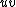 , but contains neither edge
, but contains neither edge 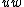 nor
nor 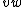 .
.
(This claim is equivalent to the relation x~y iff x not connected to y
being an equivalence relation. ~ is always
reflexive and symmetric, but only in special cases is it transitive. ~ is not transitive precisely when we have u, v and w with u ~ w and w ~ v without u ~ v.)
Assume the claim is false. Construct a new n-vertex simple graph
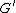 that contains no (r + 1)-clique but has more edges than
that contains no (r + 1)-clique but has more edges than 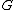 , as follows:
, as follows:Case 1:
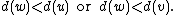
Assume that
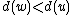 . Delete vertex
. Delete vertex 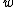 and create a copy of vertex
and create a copy of vertex  (with all of the same neighbors as
(with all of the same neighbors as  ); call it
); call it 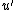 .
.Any clique in the new graph contains at most one vertex among
 .
.So this new graph does not contain any (r + 1)-clique. However, it contains more edges:

Case 2:
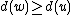 and
and 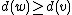
Delete vertices
 and
and  and create two new copies of vertex
and create two new copies of vertex 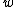 .
.Again, the new graph does not contain any (r + 1)-clique. However it contains more edges:
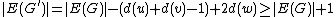 .
.This proves Claim 1.
The claim proves that one can partition the vertices of
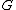 into equivalence classes based on their nonneighbors; i.e. two vertices are in the same equivalence class if they are nonadjacent. This implies that
into equivalence classes based on their nonneighbors; i.e. two vertices are in the same equivalence class if they are nonadjacent. This implies that 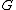
is a complete multipartite graph (where the parts are the equivalence classes).
- Claim 2: The number of edges in a complete k-partite graph is maximized when the size of the parts differs by at most one.
If G is a complete k-partite graph with parts A and B and
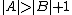 , then we can increase the number of edges in G by moving a vertex from part A to part B. By moving a vertex from part A to part B,
, then we can increase the number of edges in G by moving a vertex from part A to part B. By moving a vertex from part A to part B,the graph loses
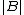 edges, but gains
edges, but gains 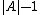 edges. Thus, it gains at least
edges. Thus, it gains at least  edge.
edge.This proves Claim 2.
This proof shows that the Turan graph has the maximum number of edges.
Additionally, the proof shows that the Turan graph is the only graph that has the maximum number of edges.
Mantel's theorem
As a special case of Turán's theorem, for r = 2, one obtains Mantel's theorem:The maximum number of edges in an n-vertex triangle-free graph
Triangle-free graph
In the mathematical area of graph theory, a triangle-free graph is an undirected graph in which no three vertices form a triangle of edges. Triangle-free graphs may be equivalently defined as graphs with clique number ≤ 2, graphs with girth ≥ 4, graphs with no induced 3-cycle, or locally...
is
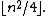
In other words, one must delete nearly half of the edges in Kn to obtain a triangle-free graph.
A strengthened form of Mantel's theorem states that any graph with at least n2/4 edges must either be the complete bipartite graph
Complete bipartite graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set.- Definition :...
Kn/2,n/2 or it must be pancyclic
Pancyclic graph
In the mathematical study of graph theory, a pancyclic graph is a directed or undirected graph that contains cycles of all possible lengths from three up to the number of vertices in the graph...
: not only does it contain a triangle, it must also contain cycles of all other possible lengths up to the number of vertices in the graph .
Another strengthening of Mantel's theorem states that the edges of any graph may be covered by at most
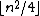 cliques
cliquesClique (graph theory)
In the mathematical area of graph theory, a clique in an undirected graph is a subset of its vertices such that every two vertices in the subset are connected by an edge. Cliques are one of the basic concepts of graph theory and are used in many other mathematical problems and constructions on graphs...
: that is, the intersection number
Intersection number (graph theory)
In the mathematical field of graph theory, the intersection number of a graph is the smallest number of elements in a representation of as an intersection graph of finite sets...
is at most
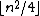 .
.See also
- Extremal graph theoryExtremal graph theoryExtremal graph theory is a branch of the mathematical field of graph theory. Extremal graph theory studies extremal graphs which satisfy a certain property. Extremality can be taken with respect to different graph invariants, such as order, size or girth...
- Erdős–Stone theoremErdos–Stone theoremIn extremal graph theory, the Erdős–Stone theorem is an asymptotic result generalising Turán's theorem to bound the number of edges in an H-free graph for a non-complete graph H...
- A probabilistic proof of Turán's theorem

