
Twisted Poincaré duality
Encyclopedia
In mathematics, the twisted Poincaré duality is a theorem removing the restriction on Poincaré duality
to oriented manifolds. The existence of a global orientation is replaced by carrying along local information, by means of a local coefficient system.
with the w- twisted fundamental class
induces Poincaré duality
isomorphisms between homology and cohomology: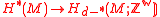 and
and 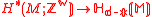 .
.
with values in the orientation bundle. This is the flat
real line bundle
denoted , that is trivialized by coordinate charts of the manifold NM, with transition maps the sign of the Jacobian determinant of the charts transition maps. As a flat line bundle
, that is trivialized by coordinate charts of the manifold NM, with transition maps the sign of the Jacobian determinant of the charts transition maps. As a flat line bundle
, it has a de Rham cohomology, denoted by or
or 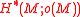 .
.
For M a compact manifold, the top degree cohomology is equipped with a so-called trace morphism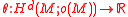 ,
,
that is to be interpreted as integration on M, ie. evaluating against the fundamental class.
The Poincaré duality for differential forms is then the conjunction, for M connected, of the following two statements:
is non-degenerate.
The oriented Poincaré duality
is contained in this statement, as understood from the fact that the orientation bundle o(M) is trivial if the manifold is oriented, an orientation being a global trivialization, ie. a nowhere vanishing parallel section.
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
to oriented manifolds. The existence of a global orientation is replaced by carrying along local information, by means of a local coefficient system.
Integer-valued formulation
Let M be a d-dimensional compact boundaryless differential manifold with orientation character w(M). Then the cap productCap product
In algebraic topology the cap product is a method of adjoining a chain of degree p with a cochain of degree q, such that q ≤ p, to form a composite chain of degree p − q. It was introduced by Eduard Čech in 1936, and independently by Hassler Whitney in 1938.-Definition:Let X be a topological...
with the w- twisted fundamental class
Fundamental class
In mathematics, the fundamental class is a homology class [M] associated to an oriented manifold M, which corresponds to "the whole manifold", and pairing with which corresponds to "integrating over the manifold"...
induces Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
isomorphisms between homology and cohomology:
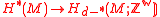 and
and 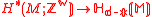 .
.Twisted Poincaré duality for de Rham cohomology
Another version of the theorem with real coefficients features the de Rham cohomologyDe Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
with values in the orientation bundle. This is the flat
Flat vector bundle
In mathematics, a vector bundle is said to be flat if it is endowed with a affine connection with vanishing curvature, ie. a flat connection.-de Rham cohomology of a flat vector bundle:...
real line bundle
Line bundle
In mathematics, a line bundle expresses the concept of a line that varies from point to point of a space. For example a curve in the plane having a tangent line at each point determines a varying line: the tangent bundle is a way of organising these...
denoted
 , that is trivialized by coordinate charts of the manifold NM, with transition maps the sign of the Jacobian determinant of the charts transition maps. As a flat line bundle
, that is trivialized by coordinate charts of the manifold NM, with transition maps the sign of the Jacobian determinant of the charts transition maps. As a flat line bundleFlat vector bundle
In mathematics, a vector bundle is said to be flat if it is endowed with a affine connection with vanishing curvature, ie. a flat connection.-de Rham cohomology of a flat vector bundle:...
, it has a de Rham cohomology, denoted by
 or
or 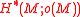 .
.For M a compact manifold, the top degree cohomology is equipped with a so-called trace morphism
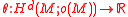 ,
,that is to be interpreted as integration on M, ie. evaluating against the fundamental class.
The Poincaré duality for differential forms is then the conjunction, for M connected, of the following two statements:
- The trace morphism is a linear isomorphism,
- The cup product, or exterior product of differential forms
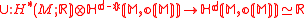
is non-degenerate.
The oriented Poincaré duality
Poincaré duality
In mathematics, the Poincaré duality theorem named after Henri Poincaré, is a basic result on the structure of the homology and cohomology groups of manifolds...
is contained in this statement, as understood from the fact that the orientation bundle o(M) is trivial if the manifold is oriented, an orientation being a global trivialization, ie. a nowhere vanishing parallel section.

