
Flat vector bundle
Encyclopedia
In mathematics
, a vector bundle
is said to be flat if it is endowed with a affine connection
with vanishing curvature
, ie. a flat connection.
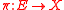 denote a flat vector bundle, and
denote a flat vector bundle, and 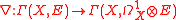 be the covariant derivative
be the covariant derivative
associated to the flat connection on E.
Let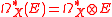 denote the vector space
denote the vector space
(in fact a sheaf of modules over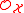 ) of differential form
) of differential form
s on X with values in E. The covariant derivative defines a degree 1 endomorphism d, the differential of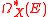 , and the flatness condition is equivalent to the property
, and the flatness condition is equivalent to the property  .
.
In other words, the graded vector space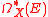 is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.
is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.
vanishes in this trivialization. An equivalent definition of a flat bundle is the choice of a trivializing atlas with locally constant transition maps.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
is said to be flat if it is endowed with a affine connection
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
with vanishing curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, ie. a flat connection.
de Rham cohomology of a flat vector bundle
Let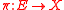 denote a flat vector bundle, and
denote a flat vector bundle, and 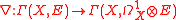 be the covariant derivative
be the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
associated to the flat connection on E.
Let
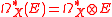 denote the vector space
denote the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
(in fact a sheaf of modules over
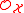 ) of differential form
) of differential formDifferential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s on X with values in E. The covariant derivative defines a degree 1 endomorphism d, the differential of
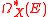 , and the flatness condition is equivalent to the property
, and the flatness condition is equivalent to the property  .
.In other words, the graded vector space
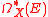 is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.
is a cochain complex. Its cohomology is called the de Rham cohomology of E, or de Rham cohomology with coefficients twisted by the local coefficient system E.Flat trivializations
A trivialization of a flat vector bundle is said to be flat if the connection formConnection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
vanishes in this trivialization. An equivalent definition of a flat bundle is the choice of a trivializing atlas with locally constant transition maps.
Examples
- Trivial line bundles can have several flat bundle structures. An example is the trivial bundle over
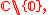 with the connection formConnection formIn mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
with the connection formConnection formIn mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
s 0 and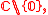 . The parallel vector fields are constant in the first case, and proportional to local determinations of the complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
. The parallel vector fields are constant in the first case, and proportional to local determinations of the complex logarithmComplex logarithmIn complex analysis, a complex logarithm function is an "inverse" of the complex exponential function, just as the natural logarithm ln x is the inverse of the real exponential function ex. Thus, a logarithm of z is a complex number w such that ew = z. The notation for such a w is log z...
in the second.
- The real canonical line bundleCanonical line bundleThe canonical or tautological line bundle on a projective space appears frequently in mathematics, often in the study of characteristic classes...
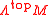 of a differential manifold M is a flat line bundle, called the orientation bundle. Its sections are volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
of a differential manifold M is a flat line bundle, called the orientation bundle. Its sections are volume formVolume formIn mathematics, a volume form on a differentiable manifold is a nowhere-vanishing differential form of top degree. Thus on a manifold M of dimension n, a volume form is an n-form, a section of the line bundle Ωn = Λn, that is nowhere equal to zero. A manifold has a volume...
s.
- A Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
is flat if, and only if, its Levi-Civita connectionLevi-Civita connectionIn Riemannian geometry, the Levi-Civita connection is a specific connection on the tangent bundle of a manifold. More specifically, it is the torsion-free metric connection, i.e., the torsion-free connection on the tangent bundle preserving a given Riemannian metric.The fundamental theorem of...
gives its tangent vector bundle a flat structure.
See also
- Vector-valued differential forms
- Local system, the more general notion of a locally constant sheaf.
- Orientation character, a characteristic form related to the orientation line bundle, useful to formulate Twisted Poincaré dualityTwisted Poincaré dualityIn mathematics, the twisted Poincaré duality is a theorem removing the restriction on Poincaré duality to oriented manifolds. The existence of a global orientation is replaced by carrying along local information, by means of a local coefficient system....
- Picard group whose connected component, the Jacobian varietyJacobian varietyIn mathematics, the Jacobian variety J of a non-singular algebraic curve C of genus g is the moduli space of degree 0 line bundles...
, is the moduli spaceModuli spaceIn algebraic geometry, a moduli space is a geometric space whose points represent algebro-geometric objects of some fixed kind, or isomorphism classes of such objects...
of algebraic flat line bundles. - MonodromyMonodromyIn mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
, or representationsGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the fundamental groupFundamental groupIn mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
by parallel transportParallel transportIn geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
on flat bundles. - HolonomyHolonomyIn differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
, the obstruction to flatness.

