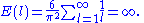Universal code (data compression)
Encyclopedia
Data compression
In computer science and information theory, data compression, source coding or bit-rate reduction is the process of encoding information using fewer bits than the original representation would use....
, a universal code for integers is a prefix code
Prefix code
A prefix code is a type of code system distinguished by its possession of the "prefix property"; which states that there is no valid code word in the system that is a prefix of any other valid code word in the set...
that maps the positive integers onto binary codewords, with the additional property that whatever the true probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
on integers, as long as the distribution is monotonic (i.e., p(i) ≥ p(i + 1) for all positive i), the expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
lengths of the codewords are within a constant factor of the expected lengths that the optimal code for that probability distribution would have assigned. A universal code is asymptotically optimal if the ratio between actual and optimal expected
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
lengths is bounded by a function of the information entropy
Information entropy
In information theory, entropy is a measure of the uncertainty associated with a random variable. In this context, the term usually refers to the Shannon entropy, which quantifies the expected value of the information contained in a message, usually in units such as bits...
of the code that, in addition to being bounded, approaches 1 as entropy approaches infinity.
In general, most prefix codes for integers assign longer codewords to larger integers. Such a code can be used to efficiently communicate a message drawn from a set of possible messages, by simply ordering the set of messages by decreasing probability and then sending the index of the intended message. Universal codes are generally not used for precisely known probability distributions, and no universal code is known to be optimal for any distribution used in practice.
These are some universal codes for integers; an asterisk (*
Asterisk
An asterisk is a typographical symbol or glyph. It is so called because it resembles a conventional image of a star. Computer scientists and mathematicians often pronounce it as star...
) indicates a code that can be trivially restated in lexicographical order
Lexicographical order
In mathematics, the lexicographic or lexicographical order, , is a generalization of the way the alphabetical order of words is based on the alphabetical order of letters.-Definition:Given two partially ordered sets A and B, the lexicographical order on...
, while a double dagger (‡) indicates a code that is asymptotically optimal:
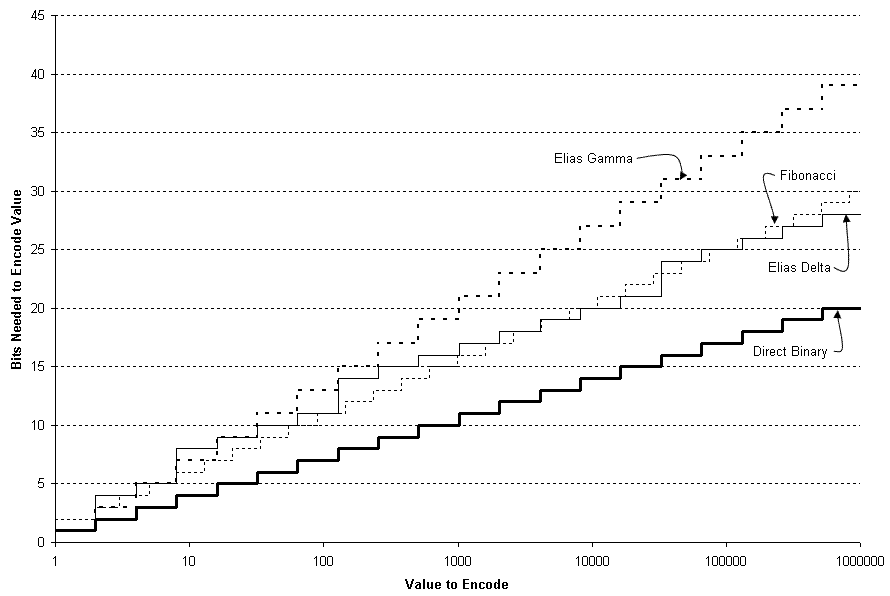
- Elias gamma codingElias gamma codingElias gamma code is a universal code encoding positive integers developed by Peter Elias. It is used most commonly when coding integers whose upper-bound cannot be determined beforehand.-Encoding:To code a number:#Write it in binary....
* - Elias delta codingElias delta codingElias delta code is a universal code encoding the positive integers developed by Peter Elias. To code a number:#Write it in binary.#Count the bits and write down that number of bits in binary ....
* ‡ - Elias omega codingElias omega codingElias omega coding is a universal code encoding the positive integers developed by Peter Elias. Like Elias gamma coding and Elias delta coding, it works by prefixing the integer with a representation of its order of magnitude in a universal code...
* ‡ - Exp-Golomb codingExponential-Golomb codingAn exponential-Golomb code of order k is a type of universal code, parameterized by a nonnegative integer k. To encode a nonnegative integer in an order-k exp-Golomb code, one can use the following method:...
*, which has Elias gamma coding as a special case. (Used in H.264/MPEG-4 AVCH.264/MPEG-4 AVCH.264/MPEG-4 Part 10 or AVC is a standard for video compression, and is currently one of the most commonly used formats for the recording, compression, and distribution of high definition video...
) - Fibonacci codingFibonacci codingIn mathematics, Fibonacci coding is a universal code which encodes positive integers into binary code words. Each code word ends with "11" and contains no other instances of "11" before the end.-Definition:...
- Levenstein coding * ‡, the original universal coding technique http://www.compression.ru/download/articles/int/levenstein_1968_on_the_redundancy_and_delay.pdf
- Byte coding , also known as comma coding, where a special bit pattern (with at least two bits) is used to mark the end of the code — for example, if an integer is encoded as a sequence of nibbleNibbleIn computing, a nibble is a four-bit aggregation, or half an octet...
s representing digits in base 15 instead of the more natural base 16, then the highest nibble value (i.e., a sequence of four ones in binary) can be used to indicate the end of the integer.
These are non-universal ones:
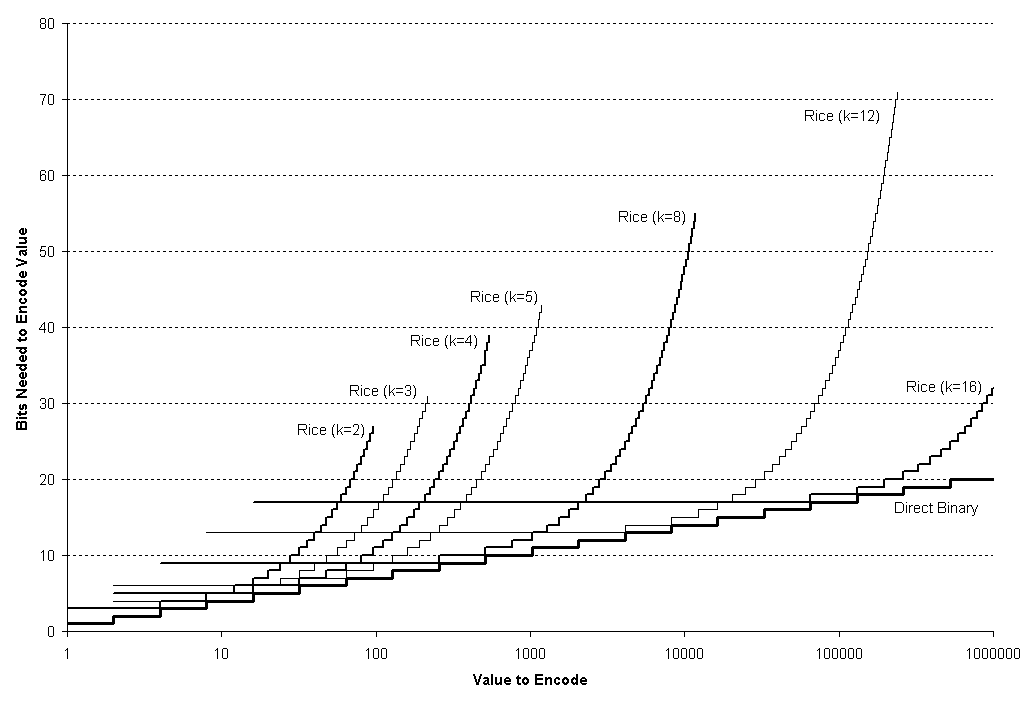
- unary codingUnary codingUnary coding, sometimes called thermometer code, is an entropy encoding that represents a natural number, n, with n ones followed by a zero or with n − 1 ones followed by a zero...
, which is used in Elias codes - Rice codingGolomb codingGolomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the...
, which is used in the FLACFLACFLAC is a codec which allows digital audio to be losslessly compressed such that file size is reduced without any information being lost...
audio codecAudio codecAll codecs are devices or computer programs capable of coding or decoding a digital data stream or signal.The term audio codec has two meanings depending on the context:...
as which has unary coding as a special case - Golomb codingGolomb codingGolomb coding is a lossless data compression method using a family of data compression codes invented by Solomon W. Golomb in the 1960s. Alphabets following a geometric distribution will have a Golomb code as an optimal prefix code, making Golomb coding highly suitable for situations in which the...
, which has Rice coding and unary coding as special cases.
Their nonuniversality can be observed by noticing that, if any of these are used to code the Gauss–Kuzmin distribution or the Zeta distribution with parameter s=2, expected codeword length is infinite. For example, using unary coding on the Zeta distribution yields an expected length of
On the other hand, using the universal Elias gamma coding for the Gauss–Kuzmin distribution results in an expected codeword length (about 3.51 bits) near entropy (about 3.43 bits)http://scholar.google.com/scholar?cluster=13442560459874106744.
A universal code should not be confused with universal source coding, in which the data compression method need not be a fixed prefix code and the ratio between actual and optimal expected lengths must approach one. However, note that an asymptotically optimal universal code can be used on independent identically-distributed sources, by using increasingly large blocks
Block code
In coding theory, block codes refers to the large and important family of error-correcting codes that encode data in blocks.There is a vast number of examples for block codes, many of which have a wide range of practical applications...
, as a method of universal source coding.
Relationship to practical compression
Huffman codingHuffman coding
In computer science and information theory, Huffman coding is an entropy encoding algorithm used for lossless data compression. The term refers to the use of a variable-length code table for encoding a source symbol where the variable-length code table has been derived in a particular way based on...
and arithmetic encoding (when they can be used) give at least as good, and often better compression than any universal code.
However, universal codes are useful when Huffman coding cannot be used — for example, when one does not know the exact probability of each message, but only knows the rankings of their probabilities.
Universal codes are also useful when Huffman codes are inconvenient. For example, when the transmitter but not the receiver knows the probabilities of the messages, Huffman coding requires an overhead of transmitting those probabilities to the receiver. Using a universal code does not have that overhead.
Each universal code, like each other self-delimiting (prefix) binary code, has its own "implied probability distribution" given by p(i)=2-l(i) where l(i) is the length of the ith codeword and p(i) is the corresponding symbol's probability. If the actual message probabilities are q(i) and Kullback–Leibler divergence
Kullback–Leibler divergence
In probability theory and information theory, the Kullback–Leibler divergence is a non-symmetric measure of the difference between two probability distributions P and Q...
DKL(q||p) is minimized by the code with l(i), then the optimal Huffman code for that set of messages will be equivalent to that code. Likewise, how close a code is to optimal can be measured by this divergence. Since universal codes are simpler and faster to encode and decode than Huffman codes (which is, in turn, simpler and faster than arithmetic encoding), the universal code would be preferable in cases where DKL(q||p) is sufficiently small.
http://www.cs.tut.fi/~albert/Dev/pucrunch/
For any geometric distribution (an exponential distribution on integers), a Golomb code is optimal. With universal codes, the implicit distribution is approximately a power law
Power law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
such as
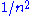(more precisely, a Zipf distribution).For the Fibonacci code, the implicit distribution is approximately
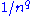, with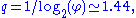
where
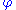is the golden ratioGolden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
. For the ternary comma code (i.e., encoding in base 3, represented with 2 bits per symbol), the implicit distribution is a power law with
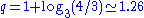. These distributions thus have near-optimal codes with their respective power laws.External links
- On-line textbook: Information Theory, Inference, and Learning Algorithms, by David MacKayDavid MacKay (scientist)David John Cameron MacKay, FRS, is the professor of natural philosophy in the department of Physics at the University of Cambridge and chief scientific adviser to the UK Department of Energy and Climate Change...
, has a chapter on codes for integers, including an accessible introduction to Elias codes.
- Кодирование целых чисел has mostly English-language papers on universal and other integer codes.