Vandermonde's identity
Encyclopedia
In combinatorics
, Vandermonde's identity, or Vandermonde's convolution, named after Alexandre-Théophile Vandermonde
(1772), states that
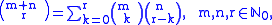
for binomial coefficient
s. This identity was given already in 1303 by the Chinese mathematician
Zhu Shijie
(Chu Shi-Chieh). See Askey 1975, pp. 59–60 for the history.
There is a q-analog
to this theorem called the q-Vandermonde identity.
s with degrees m and n, respectively, is given by
where we use the convention that ai = 0 for all integers i > m and bj = 0 for all integers j > n. By the binomial theorem
,
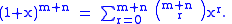
Using the binomial theorem also for the exponents m and n, and then the above formula for the product of polynomials, we obtain
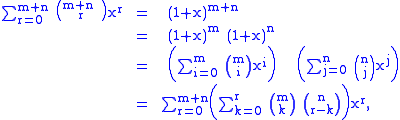
where the above convention for the coefficients of the polynomials agrees with the definition of the binomial coefficients, because both give zero for all i > m and j > n, respectively.
By comparing coefficients of xr, Vandermonde's identity follows for all integers r with 0 ≤ r ≤ m + n. For larger integers r, both sides of Vandermonde's identity are zero due to the definition of binomial coefficients.
, as follows. Suppose a committee in the US Senate
consists of m Democrat
s and n Republicans
. In how many ways can a subcommittee of r members be formed? The answer is of course
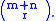
But on the other hand, the answer is the sum over all possible values of k, of the number of subcommittees consisting of k Democrats and r − k Republicans.
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, Vandermonde's identity, or Vandermonde's convolution, named after Alexandre-Théophile Vandermonde
Alexandre-Théophile Vandermonde
Alexandre-Théophile Vandermonde was a French musician, mathematician and chemist who worked with Bézout and Lavoisier; his name is now principally associated with determinant theory in mathematics. He was born in Paris, and died there.Vandermonde was a violinist, and became engaged with...
(1772), states that
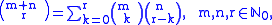
for binomial coefficient
Binomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s. This identity was given already in 1303 by the Chinese mathematician
Chinese mathematics
Mathematics in China emerged independently by the 11th century BC. The Chinese independently developed very large and negative numbers, decimals, a place value decimal system, a binary system, algebra, geometry, and trigonometry....
Zhu Shijie
Zhu Shijie
Zhu Shijie , courtesy name Hanqing , pseudonym Songting , was one of the greatest Chinese mathematicians lived during the Yuan Dynasty....
(Chu Shi-Chieh). See Askey 1975, pp. 59–60 for the history.
There is a q-analog
Q-analog
Roughly speaking, in mathematics, specifically in the areas of combinatorics and special functions, a q-analog of a theorem, identity or expression is a generalization involving a new parameter q that returns the original theorem, identity or expression in the limit as q → 1...
to this theorem called the q-Vandermonde identity.
Algebraic proof
In general, the product of two polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s with degrees m and n, respectively, is given by
where we use the convention that ai = 0 for all integers i > m and bj = 0 for all integers j > n. By the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
,
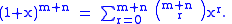
Using the binomial theorem also for the exponents m and n, and then the above formula for the product of polynomials, we obtain
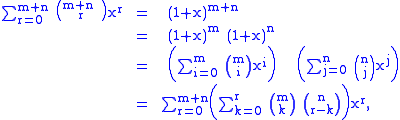
where the above convention for the coefficients of the polynomials agrees with the definition of the binomial coefficients, because both give zero for all i > m and j > n, respectively.
By comparing coefficients of xr, Vandermonde's identity follows for all integers r with 0 ≤ r ≤ m + n. For larger integers r, both sides of Vandermonde's identity are zero due to the definition of binomial coefficients.
Combinatorial proof
Vandermonde's identity also admits a more combinatorics-flavored double counting proofDouble counting (proof technique)
In combinatorics, double counting, also called counting in two ways, is a combinatorial proof technique for showing that two expressions are equal by demonstrating that they are two ways of counting the size of one set...
, as follows. Suppose a committee in the US Senate
United States Senate
The United States Senate is the upper house of the bicameral legislature of the United States, and together with the United States House of Representatives comprises the United States Congress. The composition and powers of the Senate are established in Article One of the U.S. Constitution. Each...
consists of m Democrat
Democratic Party (United States)
The Democratic Party is one of two major contemporary political parties in the United States, along with the Republican Party. The party's socially liberal and progressive platform is largely considered center-left in the U.S. political spectrum. The party has the lengthiest record of continuous...
s and n Republicans
Republican Party (United States)
The Republican Party is one of the two major contemporary political parties in the United States, along with the Democratic Party. Founded by anti-slavery expansion activists in 1854, it is often called the GOP . The party's platform generally reflects American conservatism in the U.S...
. In how many ways can a subcommittee of r members be formed? The answer is of course
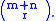
But on the other hand, the answer is the sum over all possible values of k, of the number of subcommittees consisting of k Democrats and r − k Republicans.
Generalized Vandermonde's identity
If in the algebraic derivation above more than two polynomials are used, it results in the generalized Vandermonde's identity. For y + 1 polynomials:-
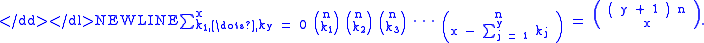
The hypergeometric probability distribution
When both sides have been divided by the expression on the left, so that the sum is 1, then the terms of the sum may be interpreted as probabilities. The resulting probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
is the hypergeometric distribution. That is the probability distribution of the number of red marbles in r draws without replacement from an urn containing n red and m blue marbles.
Chu–Vandermonde identity
The identity generalizes to non-integer arguments. In this case, it is known as the Chu–Vandermonde identity (see Askey 1975, pp. 59–60) and takes the form
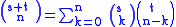
for general complex-valuedComplex numberA complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s and t and any non-negative integer n. This identity may be re-written in terms of the falling Pochhammer symbolPochhammer symbolIn mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
s as
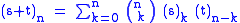
in which form it is clearly recognizable as an umbralUmbral calculusIn mathematics before the 1970s, the term umbral calculus referred to the surprising similarity between seemingly unrelated polynomial equations and certain shadowy techniques used to 'prove' them. These techniques were introduced by and are sometimes called Blissard's symbolic method...
variant of the binomial theoremBinomial theoremIn elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
. (For more on umbral variants of the binomial theorem, see binomial type) The Chu–Vandermonde identity can also be seen to be a special case of Gauss's hypergeometric theorem, which states that
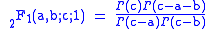
where
is the hypergeometric function and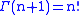 
is the gamma functionGamma functionIn mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...
. One regains the Chu–Vandermonde identity by taking a = −n and applying the identity
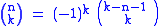
liberally.