Viscoplasticity
Encyclopedia
Viscoplasticity is a theory in continuum mechanics
that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation
of the material depends on the rate at which load
s are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation
which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep
flow as a function of time under the influence of the applied load.
The elastic response of viscoplastic materials can be represented in one-dimension by Hookean
spring
elements. Rate-dependence can be represented by nonlinear dashpot
elements in a manner similar to viscoelasticity
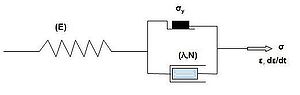
. Plasticity can be accounted for by adding sliding friction
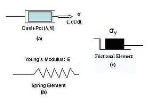
al elements as shown in Figure 1. In the figure E is the modulus of elasticity
, λ is the viscosity
parameter and N is a power-law type parameter that represents non-linear dashpot [σ(dε/dt)= σ = λ(dε/dt)(1/N)]. The sliding element can have a yield stress
(σy) that is strain rate dependent, or even constant, as shown in Figure 1c.
Viscoplasticity is usually modeled in three-dimensions using overstress models of the Perzyna or Duvaut-Lions types. In these models, the stress is allowed to increase beyond the rate-independent yield surface
upon application of a load and then allowed to relax back to the yield surface over time. The yield surface is usually assumed not to be rate-dependent in such models. An alternative approach is to add a strain rate dependence to the yield stress and use the techniques of rate independent plasticity to calculate the response of a material
For metal
s and alloy
s, viscoplasticity is the macroscopic
behavior caused by a mechanism linked to the movement of dislocation
s in grain
s, with superposed effects of inter-crystalline gliding
. The mechanism usually becomes dominant at temperatures greater than approximately one third of the absolute melting temperature. However, certain alloys exhibit viscoplasticity at room temperature (300K). For polymer
s, wood
, and bitumen, the theory of viscoplasticity is required to describe behavior beyond the limit of elasticity or viscoelasticity
.
In general, viscoplasticity theories are useful in areas such as
, Saint Venant (1870) and Levy
(1871) on the maximum shear criterion. An improved plasticity model was presented in 1913 by Von Mises
which is now referred to as the von Mises yield criterion. In viscoplasticity, the development of a mathematical model heads back to 1910 with the representation of primary creep
by Andrade's law. In 1929, Norton developed a one-dimensional dashpot model which linked the rate of secondary creep
to the stress. In 1934, Odqvist generalized Norton's law to the multi-axial case.
Concepts such as the normality of plastic flow to the yield surface and flow rules for plasticity were introduced by Prandtl (1924) and Reuss
(1930). In 1932, Hohenemser and Prager
proposed the first model for slow viscoplastic flow. This model provided a relation between the deviatoric stress and the strain rate for an incompressible Bingham solid
However, the application of these theories did not begin before 1950, where limit theorems were discovered.
In 1960, the first IUTAM Symposium “Creep in Structures” organized by Hoff provided a major development in viscoplasticity with the works of Hoff, Rabotnov, Perzyna, Hult, and Lemaitre for the isotropic hardening
laws, and those of Kratochvil, Malinini and Khadjinsky, Ponter and Leckie, and Chaboche for the kinematic hardening
laws. Perzyna, in 1963, introduced a viscosity coefficient that is temperature and time dependent. The formulated models were supported by the thermodynamics
of irreversible processes and the phenomenological
standpoint. The ideas presented in these works have been the basis for most subsequent research into rate-dependent plasticity.
is that as plastic deformation proceeds, an increase in stress is required to produce additional strain. This phenomenon is known as Strain/Work hardening
. For a viscoplastic material the hardening curves are not significantly different from those of rate-independent plastic material. Nevertheless, three essential differences can be observed.
The hypothesis of partitioning the strains by decoupling the elastic and plastic parts is still applicable where the strains are small, i.e.,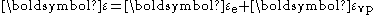
where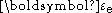 is the elastic strain and
is the elastic strain and 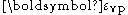 is the viscoplastic strain. To obtain the stress-strain behavior shown in blue in the figure, the material is initially loaded at a strain rate of 0.1/s. The strain rate is then instantaneously raised to 100/s and held constant at that value for some time. At the end of that time period the strain rate is dropped instantaneously back to 0.1/s and the cycle is continued for increasing values of strain. There is clearly a lag between the strain-rate change and the stress response. This lag is modeled quite accurately by overstress models (such as the Perzyna model) but not by models of rate-independent plasticity that have a rate-dependent yield stress.
is the viscoplastic strain. To obtain the stress-strain behavior shown in blue in the figure, the material is initially loaded at a strain rate of 0.1/s. The strain rate is then instantaneously raised to 100/s and held constant at that value for some time. At the end of that time period the strain rate is dropped instantaneously back to 0.1/s and the cycle is continued for increasing values of strain. There is clearly a lag between the strain-rate change and the stress response. This lag is modeled quite accurately by overstress models (such as the Perzyna model) but not by models of rate-independent plasticity that have a rate-dependent yield stress.
Creep
is the tendency of a solid material to slowly move or deform permanently under constant stresses. Creep tests measure the strain response due to a constant stress as shown in Figure 3. The classical creep curve represents the evolution of strain as a function of time in a material subjected to uniaxial stress at a constant temperature. The creep test, for instance, is performed by applying a constant force/stress and analyzing the strain response of the system. In general, as shown in Figure 3b this curve usually shows three phases or periods of behavior
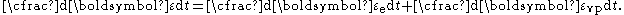
The elastic part of the strain rate is given by
For the flat region of the strain-time curve, the total strain rate is zero. Hence we have,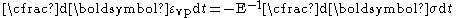
Therefore the relaxation curve can be used to determine rate of viscoplastic strain and hence the viscosity of the dashpot in a one-dimensional viscoplastic material model. The residual value that is reached when the stress has plateaued at the end of a relaxation test corresponds to the upper limit of elasticity. For some materials such as rock salt such an upper limit of elasticity occurs at a very small value of stress and relaxation tests can be continued for more than a year without any observable plateau in the stress.
It is important to note that relaxation tests are extremely difficult to perform because maintaining the condition in a test requires considerable delicacy.
in a test requires considerable delicacy.
the perfectly viscoplastic solid, the elastic perfectly viscoplastic solid, and the elastoviscoplastic hardening solid. The elements may be connected in series or in parallel. In models where the elements are connected in series the strain is additive while the stress is equal in each element. In parallel connections, the stress is additive while the strain is equal in each element. Many of these one-dimensional models can be generalized to three dimensions for the small strain regime. In the subsequent discussion, time rates strain and stress are written as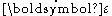 and
and  , respectively.
, respectively.
 In a perfectly viscoplastic solid, also called the Norton-Hoff model of viscoplasticity, the stress (as for viscous fluids) is a function of the rate of permanent strain. The effect of elasticity is neglected in the model, i.e.,
In a perfectly viscoplastic solid, also called the Norton-Hoff model of viscoplasticity, the stress (as for viscous fluids) is a function of the rate of permanent strain. The effect of elasticity is neglected in the model, i.e., 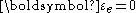 and hence there is no initial yield stress, i.e.,
and hence there is no initial yield stress, i.e.,  . The viscous dashpot has a response given by
. The viscous dashpot has a response given by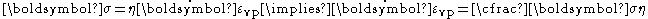
where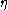 is the viscosity of the dashpot. In the Norton-Hoff model the viscosity
is the viscosity of the dashpot. In the Norton-Hoff model the viscosity  is a nonlinear function of the applied stress and is given by
is a nonlinear function of the applied stress and is given by
where is a fitting parameter, λ is the kinematic viscosity of the material and
is a fitting parameter, λ is the kinematic viscosity of the material and  . Then the viscoplastic strain rate is given by the relation
. Then the viscoplastic strain rate is given by the relation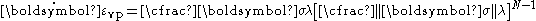
In one-dimensional form, the Norton-Hoff model can be expressed as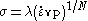
When the solid is viscoelastic.
the solid is viscoelastic.
If we assume that plastic flow is isochoric
(volume preserving), then the above relation can be expressed in the more familiar form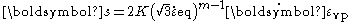
where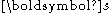 is the deviatoric stress tensor,
is the deviatoric stress tensor, 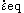 is the von Mises equivalent strain rate, and
is the von Mises equivalent strain rate, and 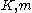 are material parameters. The equivalent strain rate is defined as
are material parameters. The equivalent strain rate is defined as
These models can be applied in metals and alloys at temperatures higher than one third of their absolute melting point (in kelvins) and polymers/asphalt at elevated temperature. The responses for strain hardening, creep, and relaxation tests of such material are shown in Figure 6.
 Two types of elementary approaches can be used to build up an elastic-perfectly viscoplastic mode. In the first situation, the sliding friction element and the dashpot are arranged in parallel and then connected in series to the elastic spring as shown in Figure 7. This model is called the Bingham-Maxwell model (by analogy with the Maxwell model
Two types of elementary approaches can be used to build up an elastic-perfectly viscoplastic mode. In the first situation, the sliding friction element and the dashpot are arranged in parallel and then connected in series to the elastic spring as shown in Figure 7. This model is called the Bingham-Maxwell model (by analogy with the Maxwell model
and the Bingham model
) or the Bingham-Norton model. In the second situation, all three elements are arranged in parallel. Such a model is called a Bingham-Kelvin model by analogy with the Kelvin model.
For elastic-perfectly viscoplastic materials, the elastic strain is no longer considered negligible but the rate of plastic strain is only a function of the initial yield stress and there is no influence of hardening. The sliding element represents a constant yielding stress when the elastic limit is exceeded irrespective of the strain. The model can be expressed as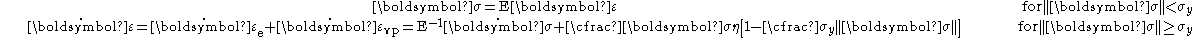
where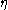 is the viscosity of the dashpot element. If the dashpot element has a response that is of the Norton form
is the viscosity of the dashpot element. If the dashpot element has a response that is of the Norton form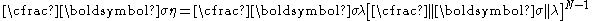
we get the Bingham-Norton model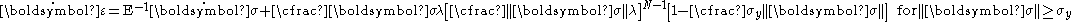
Other expressions for the strain rate can also be observed in the literature with the general form
The responses for strain hardening, creep, and relaxation tests of such material are shown in Figure 8.
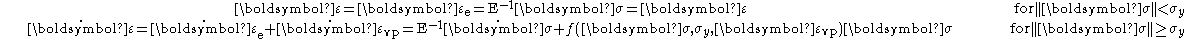 .
.
This model is adopted when metals and alloys are at medium and higher temperatures and wood under high loads. The responses for strain hardening, creep, and relaxation tests of such a material are shown in Figure 9.
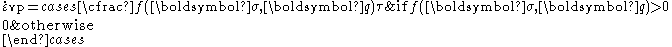
where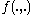 is a yield function,
is a yield function,  is the Cauchy stress,
is the Cauchy stress,  is a set of internal variables (such as the plastic strain
is a set of internal variables (such as the plastic strain 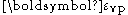 ),
),  is a relaxation time.
is a relaxation time.

where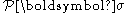 is the closest point projection of the stress state on to the boundary of the region that bounds all possible elastic stress states.
is the closest point projection of the stress state on to the boundary of the region that bounds all possible elastic stress states.
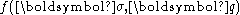 represents the evolution of the yield surface
represents the evolution of the yield surface
. The yield function is often expressed as an equation consisting of some invariant of stress and a model for the yield stress (or plastic flow stress). An examaple is von Mises or
is often expressed as an equation consisting of some invariant of stress and a model for the yield stress (or plastic flow stress). An examaple is von Mises or 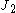 plasticity. In those situations the plastic strain rate is calculated in the same manner as in rate-independent plasticity. In other situations, the yield stress model provides a direct means of computing the plastic strain rate.
plasticity. In those situations the plastic strain rate is calculated in the same manner as in rate-independent plasticity. In other situations, the yield stress model provides a direct means of computing the plastic strain rate.
Numerous empirical and semi-empirical flow stress models are used the computational plasticity. The following temperature and strain-rate dependent models provide a sampling of the models in current use:
The Johnson–Cook (JC) model is purely empirical and is the most widely used of the five. However, this model exhibits an unrealistically small strain-rate dependence at high temperatures. The Steinberg–Cochran–Guinan–Lund (SCGL) model is semi-empirical. The model is purely empirical and strain-rate independent at high strain-rates. A dislocation-based extension based on is used at low strain-rates. The SCGL model is used extensively by the shock physics community. The Zerilli–Armstrong (ZA) model is a simple physically based model that has been used extensively. A more complex model that is based on ideas from dislocation dynamics is the Mechanical Threshold Stress (MTS) model. This model has been used to model the plastic deformation of copper, tantalum, alloys of steel, and aluminum alloys. However, the MTS model is limited to strain-rates less than around 107/s. The Preston–Tonks–Wallace (PTW) model is also physically based and has a form similar to the MTS model. However, the PTW model has components that can model plastic deformation in the overdriven shock regime (strain-rates greater that 107/s). Hence this model is valid for the largest range of strain-rates among the five flow stress models.
 )
)
where is the equivalent plastic strain,
is the equivalent plastic strain, 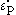 is the
is the
plastic strain-rate, and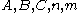 are material constants.
are material constants.
The normalized strain-rate and temperature in equation (1) are defined as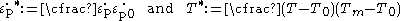
where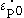 is the effective plastic strain-rate of the quasi-static test used to determine the yield and hardening parameters A,B and n. This is not as it is often thought just a parameter to make
is the effective plastic strain-rate of the quasi-static test used to determine the yield and hardening parameters A,B and n. This is not as it is often thought just a parameter to make 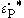 non-dimensional.
non-dimensional.  is a reference temperature, and
is a reference temperature, and  is a reference melt temperature
is a reference melt temperature
. For conditions where , we assume that
, we assume that 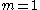 .
.
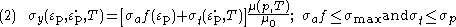
where is the athermal component of the flow stress,
is the athermal component of the flow stress,  is a function that represents strain hardening,
is a function that represents strain hardening,  is the thermally activated component of the flow stress,
is the thermally activated component of the flow stress,  is the pressure- and temperature-dependent shear modulus, and
is the pressure- and temperature-dependent shear modulus, and  is the shear modulus at standard temperature and pressure. The saturation value of the athermal stress is
is the shear modulus at standard temperature and pressure. The saturation value of the athermal stress is 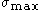 . The saturation of the thermally activated stress is the Peierls stress
. The saturation of the thermally activated stress is the Peierls stress
(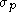 ). The shear modulus for this model is usually computed with the Steinberg–Cochran–Guinan shear modulus model.
). The shear modulus for this model is usually computed with the Steinberg–Cochran–Guinan shear modulus model.
The strain hardening function (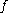 ) has the form
) has the form
where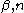 are work hardening parameters, and
are work hardening parameters, and 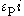 is the
is the
initial equivalent plastic strain.
The thermal component ( ) is computed using a bisection algorithm from the following equation.
) is computed using a bisection algorithm from the following equation.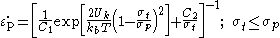
where is the energy to form a kink-pair in a dislocation segment of length
is the energy to form a kink-pair in a dislocation segment of length  ,
, 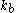 is the Boltzmann constant,
is the Boltzmann constant,  is the Peierls stress
is the Peierls stress
. The constants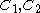 are given by the relations
are given by the relations
where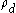 is the dislocation density
is the dislocation density
, is the length of a dislocation segment,
is the length of a dislocation segment,  is the distance between Peierls valleys,
is the distance between Peierls valleys,  is the magnitude of the Burgers vector
is the magnitude of the Burgers vector
, is the Debye frequency
is the Debye frequency
,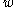 is the width of a kink loop
is the width of a kink loop
, and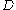 is the drag coefficient
is the drag coefficient
.
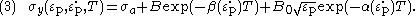
In this model, is the athermal component of the flow stress given by
is the athermal component of the flow stress given by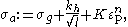
where is the contribution due to solutes and initial dislocation density,
is the contribution due to solutes and initial dislocation density, 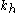 is the microstructural stress intensity,
is the microstructural stress intensity, 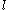 is the average grain diameter,
is the average grain diameter, 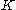 is zero for fcc materials,
is zero for fcc materials, 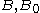 are material constants.
are material constants.
In the thermally activated terms, the functional forms of the exponents and
and 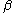 are
are
where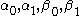 are material parameters that depend on the type of material (fcc, bcc, hcp, alloys). The Zerilli–Armstrong model has been modified by for better performance at high temperatures.
are material parameters that depend on the type of material (fcc, bcc, hcp, alloys). The Zerilli–Armstrong model has been modified by for better performance at high temperatures.
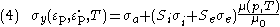
where is the athermal component of mechanical threshold stress,
is the athermal component of mechanical threshold stress, 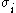 is the component of the flow stress due to intrinsic barriers to thermally activated dislocation motion and dislocation-dislocation interactions,
is the component of the flow stress due to intrinsic barriers to thermally activated dislocation motion and dislocation-dislocation interactions,  is the component of the flow stress due to microstructural evolution with increasing deformation (strain hardening), (
is the component of the flow stress due to microstructural evolution with increasing deformation (strain hardening), (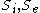 ) are temperature and strain-rate dependent scaling factors, and
) are temperature and strain-rate dependent scaling factors, and  is the shear modulus at 0 K and ambient pressure.
is the shear modulus at 0 K and ambient pressure.
The scaling factors take the Arrhenius
form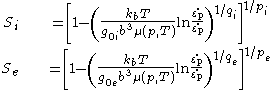
where is the Boltzmann constant,
is the Boltzmann constant,  is the magnitude of the Burgers' vector, (
is the magnitude of the Burgers' vector, (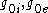 ) are normalized activation energies, (
) are normalized activation energies, ( ) are constant reference strain-rates, and (
) are constant reference strain-rates, and (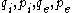 ) are constants.
) are constants.
The strain hardening component of the mechanical threshold stress ( ) is given by an empirical modified Voce law
) is given by an empirical modified Voce law
where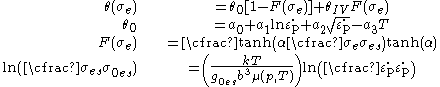
and is the hardening due to dislocation accumulation,
is the hardening due to dislocation accumulation, 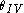 is the contribution due to stage-IV hardening, (
is the contribution due to stage-IV hardening, (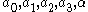 ) are constants,
) are constants, 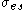 is the stress at zero strain hardening rate,
is the stress at zero strain hardening rate,  is the saturation threshold stress for deformation at 0 K,
is the saturation threshold stress for deformation at 0 K, 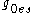 is a constant, and
is a constant, and  is the maximum strain-rate. Note that the maximum strain-rate is usually limited to about
is the maximum strain-rate. Note that the maximum strain-rate is usually limited to about  /s.
/s.

with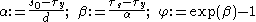
where is a normalized work-hardening saturation stress,
is a normalized work-hardening saturation stress,  is the value of
is the value of  at 0K,
at 0K,  is a normalized yield stress,
is a normalized yield stress, 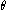 is the hardening constant in the Voce hardening law, and
is the hardening constant in the Voce hardening law, and 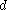 is a dimensionless material parameter that modifies the Voce hardening law.
is a dimensionless material parameter that modifies the Voce hardening law.
The saturation stress and the yield stress are given by
where is the value of
is the value of  close to the melt temperature, (
close to the melt temperature, ( ) are the values of
) are the values of 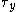 at 0 K and close to melt, respectively,
at 0 K and close to melt, respectively,  are material constants,
are material constants, 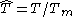 , (
, ( ) are material parameters for the high strain-rate regime, and
) are material parameters for the high strain-rate regime, and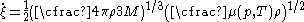
where is the density, and
is the density, and 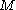 is the atomic mass.
is the atomic mass.
Continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...
that describes the rate-dependent inelastic behavior of solids. Rate-dependence in this context means that the deformation
Deformation
In materials science, deformation is a change in the shape or size of an object due to an applied force or a change in temperature...
of the material depends on the rate at which load
Structural load
Structural loads or actions are forces, deformations or accelerations applied to a structure or its components.Loads cause stresses, deformations and displacements in structures. Assessment of their effects is carried out by the methods of structural analysis...
s are applied. The inelastic behavior that is the subject of viscoplasticity is plastic deformation
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
which means that the material undergoes unrecoverable deformations when a load level is reached. Rate-dependent plasticity is important for transient plasticity calculations. The main difference between rate-independent plastic and viscoplastic material models is that the latter exhibit not only permanent deformations after the application of loads but continue to undergo a creep
Creep (deformation)
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
flow as a function of time under the influence of the applied load.
The elastic response of viscoplastic materials can be represented in one-dimension by Hookean
Hooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
spring
Spring (device)
A spring is an elastic object used to store mechanical energy. Springs are usually made out of spring steel. Small springs can be wound from pre-hardened stock, while larger ones are made from annealed steel and hardened after fabrication...
elements. Rate-dependence can be represented by nonlinear dashpot
Dashpot
A dashpot is a mechanical device, a damper which resists motion via viscous friction. The resulting force is proportional to the velocity, but acts in the opposite direction, slowing the motion and absorbing energy. It is commonly used in conjunction with a spring...
elements in a manner similar to viscoelasticity
Viscoelasticity
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just...
. Plasticity can be accounted for by adding sliding friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
al elements as shown in Figure 1. In the figure E is the modulus of elasticity
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
, λ is the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
parameter and N is a power-law type parameter that represents non-linear dashpot [σ(dε/dt)= σ = λ(dε/dt)(1/N)]. The sliding element can have a yield stress
Yield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
(σy) that is strain rate dependent, or even constant, as shown in Figure 1c.
Viscoplasticity is usually modeled in three-dimensions using overstress models of the Perzyna or Duvaut-Lions types. In these models, the stress is allowed to increase beyond the rate-independent yield surface
Yield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
upon application of a load and then allowed to relax back to the yield surface over time. The yield surface is usually assumed not to be rate-dependent in such models. An alternative approach is to add a strain rate dependence to the yield stress and use the techniques of rate independent plasticity to calculate the response of a material
For metal
Metal
A metal , is an element, compound, or alloy that is a good conductor of both electricity and heat. Metals are usually malleable and shiny, that is they reflect most of incident light...
s and alloy
Alloy
An alloy is a mixture or metallic solid solution composed of two or more elements. Complete solid solution alloys give single solid phase microstructure, while partial solutions give two or more phases that may or may not be homogeneous in distribution, depending on thermal history...
s, viscoplasticity is the macroscopic
Macroscopic
The macroscopic scale is the length scale on which objects or processes are of a size which is measurable and observable by the naked eye.When applied to phenomena and abstract objects, the macroscopic scale describes existence in the world as we perceive it, often in contrast to experiences or...
behavior caused by a mechanism linked to the movement of dislocation
Dislocation
In materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
s in grain
GRAIN
GRAIN is a small international non-profit organisation that works to support small farmers and social movements in their struggles for community-controlled and biodiversity-based food systems. Our support takes the form of independent research and analysis, networking at local, regional and...
s, with superposed effects of inter-crystalline gliding
Glide
Glide may refer to:* Glide , early 20th century American automobile company* Glide , to fly without thrust* Glide , synonym for semivowel* Glide, Oregon, census-designated place in the United States...
. The mechanism usually becomes dominant at temperatures greater than approximately one third of the absolute melting temperature. However, certain alloys exhibit viscoplasticity at room temperature (300K). For polymer
Polymer
A polymer is a large molecule composed of repeating structural units. These subunits are typically connected by covalent chemical bonds...
s, wood
Wood
Wood is a hard, fibrous tissue found in many trees. It has been used for hundreds of thousands of years for both fuel and as a construction material. It is an organic material, a natural composite of cellulose fibers embedded in a matrix of lignin which resists compression...
, and bitumen, the theory of viscoplasticity is required to describe behavior beyond the limit of elasticity or viscoelasticity
Viscoelasticity
Viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just...
.
In general, viscoplasticity theories are useful in areas such as
- the calculation of permanent deformations,
- the prediction of the plastic collapse of structures,
- the investigation of stability,
- crash simulations,
- systems exposed to high temperatures such as turbines in engines, e.g. a power plant,
- dynamic problems and systems exposed to high strain rates.
History
Research on plasticity theories started in 1864 with the work of Henri TrescaHenri Tresca
Henri Édouard Tresca was a French mechanical engineer, and a professor at the Conservatoire National des Arts et Métiers in Paris....
, Saint Venant (1870) and Levy
Levy
Levy, Lévy or Levies may refer to:* Levy * Levy's , Arizona chain* Levy County, Florida- Military organizations :* Aden Protectorate Levies* Iraq Levies* Kachin Levies* Malakand Levies* Swat Levies...
(1871) on the maximum shear criterion. An improved plasticity model was presented in 1913 by Von Mises
Von Mises
von Mises may refer to:* Ludwig von Mises Institute* von Mises distribution, named after Richard von Mises* von Mises yield criterion, named after Richard von Mises- People :* Dr...
which is now referred to as the von Mises yield criterion. In viscoplasticity, the development of a mathematical model heads back to 1910 with the representation of primary creep
Creep (deformation)
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
by Andrade's law. In 1929, Norton developed a one-dimensional dashpot model which linked the rate of secondary creep
Creep (deformation)
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
to the stress. In 1934, Odqvist generalized Norton's law to the multi-axial case.
Concepts such as the normality of plastic flow to the yield surface and flow rules for plasticity were introduced by Prandtl (1924) and Reuss
Reuss
Reuss was the name of several historical states located in present-day Thuringia, Germany. Its rulers, the Reuss family, named all of their male children Heinrich after the end of the 12th century in honour of Henry VI, Holy Roman Emperor , to whom they owed the estates of Weida and Gera...
(1930). In 1932, Hohenemser and Prager
William Prager
William Prager was a German-born US applied mathematician.He was a lecturer at Darmstadt, a deputy director at University of Göttingen, professor at Karlsruhe, University of Istanbul, the University of California, San Diego and Brown University, where he advised Bernard Budiansky.The Society of...
proposed the first model for slow viscoplastic flow. This model provided a relation between the deviatoric stress and the strain rate for an incompressible Bingham solid
Bingham plastic
A Bingham plastic is a viscoplastic material that behaves as a rigid body at low stresses but flows as a viscous fluid at high stress. It is named after Eugene C. Bingham who proposed its mathematical form....
However, the application of these theories did not begin before 1950, where limit theorems were discovered.
In 1960, the first IUTAM Symposium “Creep in Structures” organized by Hoff provided a major development in viscoplasticity with the works of Hoff, Rabotnov, Perzyna, Hult, and Lemaitre for the isotropic hardening
Work hardening
Work hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
laws, and those of Kratochvil, Malinini and Khadjinsky, Ponter and Leckie, and Chaboche for the kinematic hardening
Work hardening
Work hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
laws. Perzyna, in 1963, introduced a viscosity coefficient that is temperature and time dependent. The formulated models were supported by the thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
of irreversible processes and the phenomenological
Phenomenology (science)
The term phenomenology in science is used to describe a body of knowledge that relates empirical observations of phenomena to each other, in a way that is consistent with fundamental theory, but is not directly derived from theory. For example, we find the following definition in the Concise...
standpoint. The ideas presented in these works have been the basis for most subsequent research into rate-dependent plasticity.
Phenomenology
For a qualitative analysis, several characteristic tests are performed to describe the phenomenology of viscoplastic materials. Some examples of these tests are- hardening tests at constant stress or strain rate,
- creep tests at constant force, and
- stress relaxation at constant elongation.
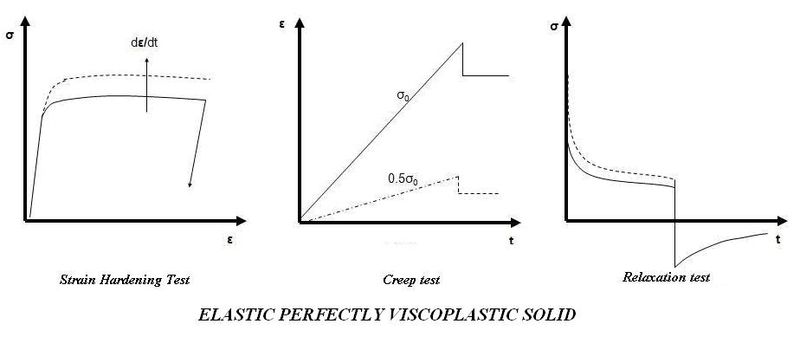
Strain hardening test
One consequence of yieldingYield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
is that as plastic deformation proceeds, an increase in stress is required to produce additional strain. This phenomenon is known as Strain/Work hardening
Work hardening
Work hardening, also known as strain hardening or cold working, is the strengthening of a metal by plastic deformation. This strengthening occurs because of dislocation movements within the crystal structure of the material. Any material with a reasonably high melting point such as metals and...
. For a viscoplastic material the hardening curves are not significantly different from those of rate-independent plastic material. Nevertheless, three essential differences can be observed.
- At the same strain, the higher the rate of strain the higher the stress
- A change in the rate of strain during the test results in an immediate change in the stress–strain curve.
- The concept of a plastic yield limitYield (engineering)The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
is no longer strictly applicable.
The hypothesis of partitioning the strains by decoupling the elastic and plastic parts is still applicable where the strains are small, i.e.,
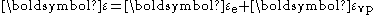
where
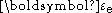 is the elastic strain and
is the elastic strain and 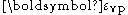 is the viscoplastic strain. To obtain the stress-strain behavior shown in blue in the figure, the material is initially loaded at a strain rate of 0.1/s. The strain rate is then instantaneously raised to 100/s and held constant at that value for some time. At the end of that time period the strain rate is dropped instantaneously back to 0.1/s and the cycle is continued for increasing values of strain. There is clearly a lag between the strain-rate change and the stress response. This lag is modeled quite accurately by overstress models (such as the Perzyna model) but not by models of rate-independent plasticity that have a rate-dependent yield stress.
is the viscoplastic strain. To obtain the stress-strain behavior shown in blue in the figure, the material is initially loaded at a strain rate of 0.1/s. The strain rate is then instantaneously raised to 100/s and held constant at that value for some time. At the end of that time period the strain rate is dropped instantaneously back to 0.1/s and the cycle is continued for increasing values of strain. There is clearly a lag between the strain-rate change and the stress response. This lag is modeled quite accurately by overstress models (such as the Perzyna model) but not by models of rate-independent plasticity that have a rate-dependent yield stress.Creep test
 |
Creep
Creep (deformation)
In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
is the tendency of a solid material to slowly move or deform permanently under constant stresses. Creep tests measure the strain response due to a constant stress as shown in Figure 3. The classical creep curve represents the evolution of strain as a function of time in a material subjected to uniaxial stress at a constant temperature. The creep test, for instance, is performed by applying a constant force/stress and analyzing the strain response of the system. In general, as shown in Figure 3b this curve usually shows three phases or periods of behavior
- A primary creep stage, also known as transient creep, is the starting stage during which hardening of the material leads to a decrease in the rate of flow which is initially very high.
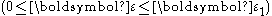 .
. - The secondary creep stage, also known as the steady state, is where the strain rate is constant.
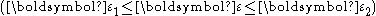 .
. - A tertiary creep phase in which there is an increase in the strain rate up to the fracture strain.
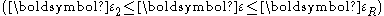 .
.
Relaxation test
As shown in Figure 4, the relaxation test is defined as the stress response due to a constant strain for a period of time. In viscoplastic materials, relaxation tests demonstrate the stress relaxation in uniaxial loading at a constant strain. In fact, these tests characterize the viscosity and can be used to determine the relation which exists between the stress and the rate of viscoplastic strain. The decompositon of strain rate is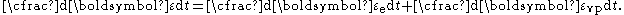
The elastic part of the strain rate is given by

For the flat region of the strain-time curve, the total strain rate is zero. Hence we have,
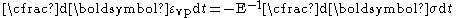
Therefore the relaxation curve can be used to determine rate of viscoplastic strain and hence the viscosity of the dashpot in a one-dimensional viscoplastic material model. The residual value that is reached when the stress has plateaued at the end of a relaxation test corresponds to the upper limit of elasticity. For some materials such as rock salt such an upper limit of elasticity occurs at a very small value of stress and relaxation tests can be continued for more than a year without any observable plateau in the stress.
It is important to note that relaxation tests are extremely difficult to perform because maintaining the condition
 in a test requires considerable delicacy.
in a test requires considerable delicacy.Rheological models of viscoplasticity
One-dimensional constitutive models for viscoplasticity based on spring-dashpot-slider elements includethe perfectly viscoplastic solid, the elastic perfectly viscoplastic solid, and the elastoviscoplastic hardening solid. The elements may be connected in series or in parallel. In models where the elements are connected in series the strain is additive while the stress is equal in each element. In parallel connections, the stress is additive while the strain is equal in each element. Many of these one-dimensional models can be generalized to three dimensions for the small strain regime. In the subsequent discussion, time rates strain and stress are written as
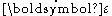 and
and  , respectively.
, respectively.Perfectly viscoplastic solid (Norton-Hoff model)

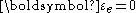 and hence there is no initial yield stress, i.e.,
and hence there is no initial yield stress, i.e.,  . The viscous dashpot has a response given by
. The viscous dashpot has a response given by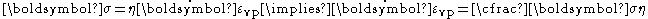
where
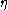 is the viscosity of the dashpot. In the Norton-Hoff model the viscosity
is the viscosity of the dashpot. In the Norton-Hoff model the viscosity  is a nonlinear function of the applied stress and is given by
is a nonlinear function of the applied stress and is given by
where
 is a fitting parameter, λ is the kinematic viscosity of the material and
is a fitting parameter, λ is the kinematic viscosity of the material and  . Then the viscoplastic strain rate is given by the relation
. Then the viscoplastic strain rate is given by the relation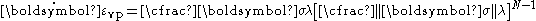
In one-dimensional form, the Norton-Hoff model can be expressed as
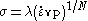
When
 the solid is viscoelastic.
the solid is viscoelastic.If we assume that plastic flow is isochoric
Isochoric
Isochoric may refer to:*cell-transitive, in geometry*isochoric process, in chemistry or thermodynamics...
(volume preserving), then the above relation can be expressed in the more familiar form
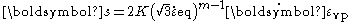
where
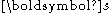 is the deviatoric stress tensor,
is the deviatoric stress tensor, 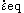 is the von Mises equivalent strain rate, and
is the von Mises equivalent strain rate, and 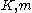 are material parameters. The equivalent strain rate is defined as
are material parameters. The equivalent strain rate is defined as
These models can be applied in metals and alloys at temperatures higher than one third of their absolute melting point (in kelvins) and polymers/asphalt at elevated temperature. The responses for strain hardening, creep, and relaxation tests of such material are shown in Figure 6.
 |
Elastic perfectly viscoplastic solid (Bingham-Norton model)

Maxwell material
A Maxwell material is a viscoelastic material having the properties both of elasticity and viscosity. It is named for James Clerk Maxwell who proposed the model in 1867. It is also known as a Maxwell fluid.- Definition :...
and the Bingham model
Bingham plastic
A Bingham plastic is a viscoplastic material that behaves as a rigid body at low stresses but flows as a viscous fluid at high stress. It is named after Eugene C. Bingham who proposed its mathematical form....
) or the Bingham-Norton model. In the second situation, all three elements are arranged in parallel. Such a model is called a Bingham-Kelvin model by analogy with the Kelvin model.
For elastic-perfectly viscoplastic materials, the elastic strain is no longer considered negligible but the rate of plastic strain is only a function of the initial yield stress and there is no influence of hardening. The sliding element represents a constant yielding stress when the elastic limit is exceeded irrespective of the strain. The model can be expressed as
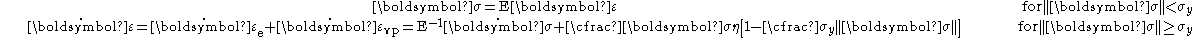
where
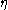 is the viscosity of the dashpot element. If the dashpot element has a response that is of the Norton form
is the viscosity of the dashpot element. If the dashpot element has a response that is of the Norton form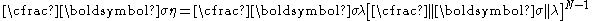
we get the Bingham-Norton model
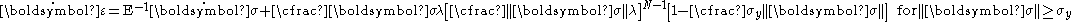
Other expressions for the strain rate can also be observed in the literature with the general form

The responses for strain hardening, creep, and relaxation tests of such material are shown in Figure 8.
 |
Elastoviscoplastic hardening solid
An elastic-viscoplastic material with strain hardening is described by equations similar to those for a elastic-viscoplastic material with perfect plasticity. However, in this case the stress depends both on the plastic strain rate and on the plastic strain itself. For an elastoviscoplastic material the stress, after exceeding the yield stress, continues to increase beyond the initial yielding point. This implies that the yield stress in the sliding element increases with strain and the model may be expressed in generic terms as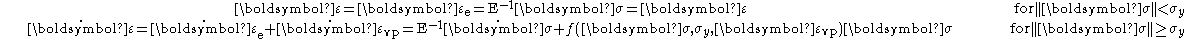 .
.This model is adopted when metals and alloys are at medium and higher temperatures and wood under high loads. The responses for strain hardening, creep, and relaxation tests of such a material are shown in Figure 9.
 |
Strain-rate dependent plasticity models
Classical phenomenological viscoplasticity models for small strains are usually categorized into two types:- the Perzyna formulation
- the Duvaut–Lions formulation
Perzyna formulation
In the Perzyna formulation the plastic strain rate is assumed to be given by a constitutive relation of the form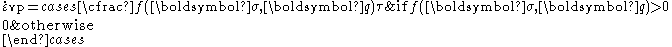
where
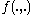 is a yield function,
is a yield function,  is the Cauchy stress,
is the Cauchy stress,  is a set of internal variables (such as the plastic strain
is a set of internal variables (such as the plastic strain 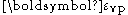 ),
),  is a relaxation time.
is a relaxation time.Duvaut–Lions formulation
The Duvaut–Lions formulation is equivalent to the Perzyna formulation and may be expressed as
where
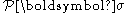 is the closest point projection of the stress state on to the boundary of the region that bounds all possible elastic stress states.
is the closest point projection of the stress state on to the boundary of the region that bounds all possible elastic stress states.Flow stress models
The quantity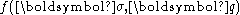 represents the evolution of the yield surface
represents the evolution of the yield surfaceYield surface
A yield surface is a five-dimensional surface in the six-dimensional space of stresses. The yield surface is usually convex and the state of stress of inside the yield surface is elastic. When the stress state lies on the surface the material is said to have reached its yield point and the...
. The yield function
 is often expressed as an equation consisting of some invariant of stress and a model for the yield stress (or plastic flow stress). An examaple is von Mises or
is often expressed as an equation consisting of some invariant of stress and a model for the yield stress (or plastic flow stress). An examaple is von Mises or 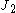 plasticity. In those situations the plastic strain rate is calculated in the same manner as in rate-independent plasticity. In other situations, the yield stress model provides a direct means of computing the plastic strain rate.
plasticity. In those situations the plastic strain rate is calculated in the same manner as in rate-independent plasticity. In other situations, the yield stress model provides a direct means of computing the plastic strain rate.Numerous empirical and semi-empirical flow stress models are used the computational plasticity. The following temperature and strain-rate dependent models provide a sampling of the models in current use:
- the Johnson–Cook model
- the Steinberg–Cochran–Guinan–Lund model.
- the Zerilli–Armstrong model.
- the Mechanical Threshold Stress model.
- the Preston–Tonks–Wallace model.
The Johnson–Cook (JC) model is purely empirical and is the most widely used of the five. However, this model exhibits an unrealistically small strain-rate dependence at high temperatures. The Steinberg–Cochran–Guinan–Lund (SCGL) model is semi-empirical. The model is purely empirical and strain-rate independent at high strain-rates. A dislocation-based extension based on is used at low strain-rates. The SCGL model is used extensively by the shock physics community. The Zerilli–Armstrong (ZA) model is a simple physically based model that has been used extensively. A more complex model that is based on ideas from dislocation dynamics is the Mechanical Threshold Stress (MTS) model. This model has been used to model the plastic deformation of copper, tantalum, alloys of steel, and aluminum alloys. However, the MTS model is limited to strain-rates less than around 107/s. The Preston–Tonks–Wallace (PTW) model is also physically based and has a form similar to the MTS model. However, the PTW model has components that can model plastic deformation in the overdriven shock regime (strain-rates greater that 107/s). Hence this model is valid for the largest range of strain-rates among the five flow stress models.
Johnson–Cook flow stress model
The Johnson–Cook (JC) model is purely empirical and gives the following relation for the flow stress ( )
)
where
 is the equivalent plastic strain,
is the equivalent plastic strain, 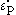 is the
is theplastic strain-rate, and
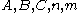 are material constants.
are material constants.The normalized strain-rate and temperature in equation (1) are defined as
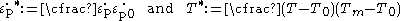
where
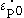 is the effective plastic strain-rate of the quasi-static test used to determine the yield and hardening parameters A,B and n. This is not as it is often thought just a parameter to make
is the effective plastic strain-rate of the quasi-static test used to determine the yield and hardening parameters A,B and n. This is not as it is often thought just a parameter to make 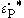 non-dimensional.
non-dimensional.  is a reference temperature, and
is a reference temperature, and  is a reference melt temperature
is a reference melt temperatureMelting point
The melting point of a solid is the temperature at which it changes state from solid to liquid. At the melting point the solid and liquid phase exist in equilibrium. The melting point of a substance depends on pressure and is usually specified at standard atmospheric pressure...
. For conditions where
 , we assume that
, we assume that 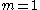 .
.Steinberg–Cochran–Guinan–Lund flow stress model
The Steinberg–Cochran–Guinan–Lund (SCGL) model is a semi-empirical model that was developed by Steinberg et al. for high strain-rate situations and extended to low strain-rates and bcc materials by Steinberg and Lund. The flow stress in this model is given by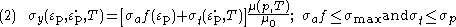
where
 is the athermal component of the flow stress,
is the athermal component of the flow stress,  is a function that represents strain hardening,
is a function that represents strain hardening,  is the thermally activated component of the flow stress,
is the thermally activated component of the flow stress,  is the pressure- and temperature-dependent shear modulus, and
is the pressure- and temperature-dependent shear modulus, and  is the shear modulus at standard temperature and pressure. The saturation value of the athermal stress is
is the shear modulus at standard temperature and pressure. The saturation value of the athermal stress is 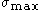 . The saturation of the thermally activated stress is the Peierls stress
. The saturation of the thermally activated stress is the Peierls stressPeierls Stress
Peierls stress is the force needed to move a dislocation within a plane of atoms in the unit cell. The magnitude varies periodically as the dislocation moves within the plane. Peierls stress depends on the size and width of a dislocation and the distance between planes...
(
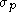 ). The shear modulus for this model is usually computed with the Steinberg–Cochran–Guinan shear modulus model.
). The shear modulus for this model is usually computed with the Steinberg–Cochran–Guinan shear modulus model.The strain hardening function (
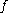 ) has the form
) has the form
where
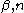 are work hardening parameters, and
are work hardening parameters, and 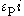 is the
is theinitial equivalent plastic strain.
The thermal component (
 ) is computed using a bisection algorithm from the following equation.
) is computed using a bisection algorithm from the following equation.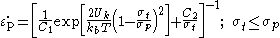
where
 is the energy to form a kink-pair in a dislocation segment of length
is the energy to form a kink-pair in a dislocation segment of length  ,
, 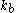 is the Boltzmann constant,
is the Boltzmann constant,  is the Peierls stress
is the Peierls stressPeierls Stress
Peierls stress is the force needed to move a dislocation within a plane of atoms in the unit cell. The magnitude varies periodically as the dislocation moves within the plane. Peierls stress depends on the size and width of a dislocation and the distance between planes...
. The constants
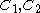 are given by the relations
are given by the relations
where
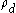 is the dislocation density
is the dislocation densityDislocation
In materials science, a dislocation is a crystallographic defect, or irregularity, within a crystal structure. The presence of dislocations strongly influences many of the properties of materials...
,
 is the length of a dislocation segment,
is the length of a dislocation segment,  is the distance between Peierls valleys,
is the distance between Peierls valleys,  is the magnitude of the Burgers vector
is the magnitude of the Burgers vectorBurgers vector
The Burgers vector, named after Dutch physicist Jan Burgers, is a vector, often denoted b, that represents the magnitude and direction of the lattice distortion of dislocation in a crystal lattice....
,
 is the Debye frequency
is the Debye frequencyDebye frequency
The Debye frequency of a crystal is a theoretical maximum frequency of vibration for the atoms that make up the crystal . It was proposed by Peter Debye as part of the Debye model. It is generally not the same as the actual maximum oscillation frequency for the crystal, due to approximations in the...
,
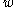 is the width of a kink loop
is the width of a kink loopPinning points
In a crystalline material, a dislocation is capable of traveling throughout the lattice when relatively small stresses are applied. This movement of dislocations results in the material plastically deforming. Pinning points in the material act to halt a dislocation's movement, requiring a greater...
, and
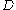 is the drag coefficient
is the drag coefficientDrag coefficient
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
.
Zerilli–Armstrong flow stress model
The Zerilli–Armstrong (ZA) model is based on simplified dislocation mechanics. The general form of the equation for the flow stress is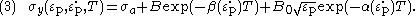
In this model,
 is the athermal component of the flow stress given by
is the athermal component of the flow stress given by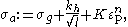
where
 is the contribution due to solutes and initial dislocation density,
is the contribution due to solutes and initial dislocation density, 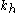 is the microstructural stress intensity,
is the microstructural stress intensity, 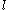 is the average grain diameter,
is the average grain diameter, 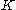 is zero for fcc materials,
is zero for fcc materials, 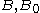 are material constants.
are material constants.In the thermally activated terms, the functional forms of the exponents
 and
and 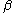 are
are
where
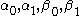 are material parameters that depend on the type of material (fcc, bcc, hcp, alloys). The Zerilli–Armstrong model has been modified by for better performance at high temperatures.
are material parameters that depend on the type of material (fcc, bcc, hcp, alloys). The Zerilli–Armstrong model has been modified by for better performance at high temperatures.Mechanical threshold stress flow stress model
The Mechanical Threshold Stress (MTS) model ) has the form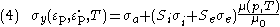
where
 is the athermal component of mechanical threshold stress,
is the athermal component of mechanical threshold stress, 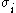 is the component of the flow stress due to intrinsic barriers to thermally activated dislocation motion and dislocation-dislocation interactions,
is the component of the flow stress due to intrinsic barriers to thermally activated dislocation motion and dislocation-dislocation interactions,  is the component of the flow stress due to microstructural evolution with increasing deformation (strain hardening), (
is the component of the flow stress due to microstructural evolution with increasing deformation (strain hardening), (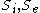 ) are temperature and strain-rate dependent scaling factors, and
) are temperature and strain-rate dependent scaling factors, and  is the shear modulus at 0 K and ambient pressure.
is the shear modulus at 0 K and ambient pressure.The scaling factors take the Arrhenius
Arrhenius equation
The Arrhenius equation is a simple, but remarkably accurate, formula for the temperature dependence of the reaction rate constant, and therefore, rate of a chemical reaction. The equation was first proposed by the Dutch chemist J. H. van 't Hoff in 1884; five years later in 1889, the Swedish...
form
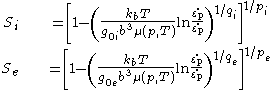
where
 is the Boltzmann constant,
is the Boltzmann constant,  is the magnitude of the Burgers' vector, (
is the magnitude of the Burgers' vector, (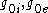 ) are normalized activation energies, (
) are normalized activation energies, ( ) are constant reference strain-rates, and (
) are constant reference strain-rates, and (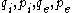 ) are constants.
) are constants.The strain hardening component of the mechanical threshold stress (
 ) is given by an empirical modified Voce law
) is given by an empirical modified Voce law
where
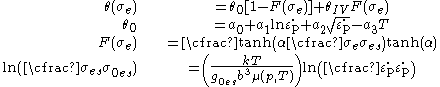
and
 is the hardening due to dislocation accumulation,
is the hardening due to dislocation accumulation, 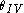 is the contribution due to stage-IV hardening, (
is the contribution due to stage-IV hardening, (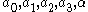 ) are constants,
) are constants, 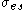 is the stress at zero strain hardening rate,
is the stress at zero strain hardening rate,  is the saturation threshold stress for deformation at 0 K,
is the saturation threshold stress for deformation at 0 K, 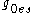 is a constant, and
is a constant, and  is the maximum strain-rate. Note that the maximum strain-rate is usually limited to about
is the maximum strain-rate. Note that the maximum strain-rate is usually limited to about  /s.
/s.Preston–Tonks–Wallace flow stress model
The Preston–Tonks–Wallace (PTW) model attempts to provide a model for the flow stress for extreme strain-rates (up to 1011/s) and temperatures up to melt. A linear Voce hardening law is used in the model. The PTW flow stress is given by
with
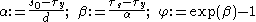
where
 is a normalized work-hardening saturation stress,
is a normalized work-hardening saturation stress,  is the value of
is the value of  at 0K,
at 0K,  is a normalized yield stress,
is a normalized yield stress, 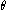 is the hardening constant in the Voce hardening law, and
is the hardening constant in the Voce hardening law, and 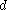 is a dimensionless material parameter that modifies the Voce hardening law.
is a dimensionless material parameter that modifies the Voce hardening law.The saturation stress and the yield stress are given by

where
 is the value of
is the value of  close to the melt temperature, (
close to the melt temperature, ( ) are the values of
) are the values of 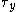 at 0 K and close to melt, respectively,
at 0 K and close to melt, respectively,  are material constants,
are material constants, 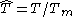 , (
, ( ) are material parameters for the high strain-rate regime, and
) are material parameters for the high strain-rate regime, and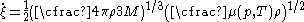
where
 is the density, and
is the density, and 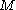 is the atomic mass.
is the atomic mass.See also
- ViscoelasticityViscoelasticityViscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like honey, resist shear flow and strain linearly with time when a stress is applied. Elastic materials strain instantaneously when stretched and just...
- Bingham plasticBingham plasticA Bingham plastic is a viscoplastic material that behaves as a rigid body at low stresses but flows as a viscous fluid at high stress. It is named after Eugene C. Bingham who proposed its mathematical form....
- DashpotDashpotA dashpot is a mechanical device, a damper which resists motion via viscous friction. The resulting force is proportional to the velocity, but acts in the opposite direction, slowing the motion and absorbing energy. It is commonly used in conjunction with a spring...
- Creep (deformation)Creep (deformation)In materials science, creep is the tendency of a solid material to slowly move or deform permanently under the influence of stresses. It occurs as a result of long term exposure to high levels of stress that are below the yield strength of the material....
- Plasticity (physics)Plasticity (physics)In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
- Continuum mechanicsContinuum mechanicsContinuum mechanics is a branch of mechanics that deals with the analysis of the kinematics and the mechanical behavior of materials modelled as a continuous mass rather than as discrete particles...

