
Witten index
Encyclopedia
In quantum field theory
and statistical mechanics
, the Witten index at the inverse temperature β is defined as a modification of the standard partition function:
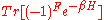
Note the (-1)F
operator, where F is the fermion
number operator. This is what makes it different from the ordinary partition function
.
In a supersymmetric
theory, each nonzero energy eigenvalue contains an equal number of bosonic and fermionic states. Because of this, the Witten index is independent of the temperature and gives the number of zero energy bosonic vacuum state
s minus the number of zero energy fermionic vacuum states. In particular, if supersymmetry is spontaneously broken
then there are no zero energy ground states and so the Witten index is equal to zero.
The Witten index of a supersymmetric field theory is an example of a quasi-topological quantity, which is a quantity that depends only on F-term
s and not on D-term
s in the Lagrangian
. A more refined invariant in 2-dimensional theories, constructing using only the right-moving part of the fermion number operator together with a 2-parameter family of variations, is the elliptic genus
.
Quantum field theory
Quantum field theory provides a theoretical framework for constructing quantum mechanical models of systems classically parametrized by an infinite number of dynamical degrees of freedom, that is, fields and many-body systems. It is the natural and quantitative language of particle physics and...
and statistical mechanics
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
, the Witten index at the inverse temperature β is defined as a modification of the standard partition function:
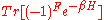
Note the (-1)F
(-1)^F
In a quantum field theory with fermions, F is a unitary, Hermitian, involutive operator which multiplies bosonic states by 1 and fermionic states by −1. This is always a global internal symmetry of any quantum field theory with fermions and corresponds to a rotation by 2π. This splits the Hilbert...
operator, where F is the fermion
Fermion
In particle physics, a fermion is any particle which obeys the Fermi–Dirac statistics . Fermions contrast with bosons which obey Bose–Einstein statistics....
number operator. This is what makes it different from the ordinary partition function
Partition function (mathematics)
The partition function or configuration integral, as used in probability theory, information science and dynamical systems, is an abstraction of the definition of a partition function in statistical mechanics. It is a special case of a normalizing constant in probability theory, for the Boltzmann...
.
In a supersymmetric
Supersymmetry
In particle physics, supersymmetry is a symmetry that relates elementary particles of one spin to other particles that differ by half a unit of spin and are known as superpartners...
theory, each nonzero energy eigenvalue contains an equal number of bosonic and fermionic states. Because of this, the Witten index is independent of the temperature and gives the number of zero energy bosonic vacuum state
Vacuum state
In quantum field theory, the vacuum state is the quantum state with the lowest possible energy. Generally, it contains no physical particles...
s minus the number of zero energy fermionic vacuum states. In particular, if supersymmetry is spontaneously broken
Supersymmetry breaking
In particle physics, supersymmetry breaking is the process to obtain a seemingly non-supersymmetric physics from a supersymmetric theory which is a necessary step to reconcile supersymmetry with actual experiments. It is an example of spontaneous symmetry breaking...
then there are no zero energy ground states and so the Witten index is equal to zero.
The Witten index of a supersymmetric field theory is an example of a quasi-topological quantity, which is a quantity that depends only on F-term
F-term
In theoretical physics, one often analyzes theories with supersymmetry in which F-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s and not on D-term
D-term
In theoretical physics, one often analyzes theories with supersymmetry in which D-terms play an important role. In four dimensions, the minimal N=1 supersymmetry may be written using a superspace. This superspace involves four extra fermionic coordinates \theta^1,\theta^2,\bar\theta^1,\bar\theta^2,...
s in the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
. A more refined invariant in 2-dimensional theories, constructing using only the right-moving part of the fermion number operator together with a 2-parameter family of variations, is the elliptic genus
Genus of a multiplicative sequence
In mathematics, the genus of a multiplicative sequence is a ring homomorphism, from the cobordism ring of smooth oriented compact manifolds to another ring, usually the ring of rational numbers.-Definition:...
.

