Yangian
Encyclopedia
Yangian is an important structure in modern representation theory
, a type of a quantum group
with origins in physics
. Yangians first appeared in the work of Ludvig Faddeev
and his school concerning the quantum inverse scattering method
in the late 1970s and early 1980s. Initially they were considered a convenient tool to generate the solutions of the quantum Yang–Baxter equation. The name Yangian was introduced by Vladimir Drinfeld in 1985 in honor of C.N. Yang. The center of Yangian can be described by quantum determinant.
Y(a), called the Yangian of a. This Hopf algebra is a deformation of the universal enveloping algebra
U(a[z]) of the Lie algebra of polynomial loops of a given by explicit generators and relations. The relations can be encoded by identities involving a rational R-matrix
. Replacing it with a trigonometric R-matrix, one arrives at affine quantum groups, defined in the same paper of Drinfeld
.
In the case of the general linear Lie algebra
glN, the Yangian admits a simpler description in terms of a single ternary (or RTT) relation on the matrix generators due to Faddeev and coauthors.
The Yangian Y(glN) is defined to be the algebra generated by elements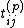
with 1 ≤ i, j ≤ N and p ≥ 0, subject to the relations
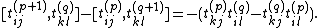
Defining
, setting
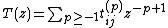
and introducing the R-matrix
R(z) = I + z−1 P on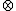 CN
CN,
where P is the operator permuting the tensor factors, the above relations can be written more simply as the ternary relation:
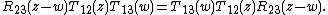
The Yangian becomes a Hopf algebra
with comultiplication Δ, counit ε and antipode s given by
At special values of the spectral parameter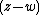
, the R-matrix degenerates to a rank one projection. This can be used to define the quantum determinant of 
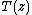, which generates the center of the Yangian.
The twisted Yangian Y–(gl2N), introduced by G. I. Olshansky, is the sub-Hopf algebra generated by the coefficients of
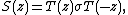
where σ is the involution of gl2N given by
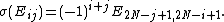
Quantum determinant is the center of Yangian.
later discovered a generalization of this theory to other classical Lie algebra
s, based on the twisted Yangian.
Yangian also appears as a symmetry group of one dimensional exactly solvable models such as spin chains
, Hubbard model and in models of one dimensional relativistic quantum field theory.
between representations of general linear and symmetric group
s that involves the Yangian of slN and the degenerate affine Hecke algebra (graded Hecke algebra of type A, in George Lusztig's terminology).
Representations of Yangians have been extensively studied, but the theory is still under active development.
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
, a type of a quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
with origins in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
. Yangians first appeared in the work of Ludvig Faddeev
Ludvig Faddeev
-References:...
and his school concerning the quantum inverse scattering method
Quantum inverse scattering method
Quantum inverse scattering method relates two different approaches:1) Inverse scattering transform is a method of solving classical integrable differential equations of evolutionary type.Important concept is Lax representation....
in the late 1970s and early 1980s. Initially they were considered a convenient tool to generate the solutions of the quantum Yang–Baxter equation. The name Yangian was introduced by Vladimir Drinfeld in 1985 in honor of C.N. Yang. The center of Yangian can be described by quantum determinant.
Description
For any finite-dimensional semisimple Lie algebra a, Drinfeld defined an infinite-dimensional Hopf algebraHopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
Y(a), called the Yangian of a. This Hopf algebra is a deformation of the universal enveloping algebra
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
U(a[z]) of the Lie algebra of polynomial loops of a given by explicit generators and relations. The relations can be encoded by identities involving a rational R-matrix
R-matrix
The term R-matrix has several meanings, depending on the field of study.The term R-matrix is used in connection with the Yang–Baxter equation. This is an equation which was first introduced in the field of statistical mechanics, taking its name from independent work of C. N. Yang and R. J....
. Replacing it with a trigonometric R-matrix, one arrives at affine quantum groups, defined in the same paper of Drinfeld
Vladimir Drinfel'd
Vladimir Gershonovich Drinfel'd is a Ukrainian and Soviet mathematician at the University of Chicago.The work of Drinfeld related algebraic geometry over finite fields with number theory, especially the theory of automorphic forms, through the notions of elliptic module and the theory of the...
.
In the case of the general linear Lie algebra
General linear group
In mathematics, the general linear group of degree n is the set of n×n invertible matrices, together with the operation of ordinary matrix multiplication. This forms a group, because the product of two invertible matrices is again invertible, and the inverse of an invertible matrix is invertible...
glN, the Yangian admits a simpler description in terms of a single ternary (or RTT) relation on the matrix generators due to Faddeev and coauthors.
The Yangian Y(glN) is defined to be the algebra generated by elements
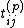with 1 ≤ i, j ≤ N and p ≥ 0, subject to the relations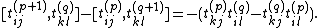Defining
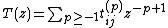
, settingand introducing the R-matrix
R-matrix
The term R-matrix has several meanings, depending on the field of study.The term R-matrix is used in connection with the Yang–Baxter equation. This is an equation which was first introduced in the field of statistical mechanics, taking its name from independent work of C. N. Yang and R. J....
R(z) = I + z−1 P on 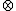CN
CN,where P is the operator permuting the tensor factors, the above relations can be written more simply as the ternary relation:
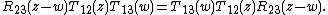
The Yangian becomes a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
with comultiplication Δ, counit ε and antipode s given by
At special values of the spectral parameter
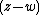, the R-matrix degenerates to a rank one projection. This can be used to define the quantum determinant of 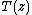, which generates the center of the Yangian.The twisted Yangian Y–(gl2N), introduced by G. I. Olshansky, is the sub-Hopf algebra generated by the coefficients of
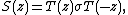
where σ is the involution of gl2N given by
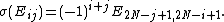
Quantum determinant is the center of Yangian.
Applications to classical representation theory
G.I. Olshansky and I.Cherednik discovered that the Yangian of glN is closely related with the branching properties of irreducible finite-dimensional representations of general linear algebras. In particular, the classical Gelfand–Tsetlin construction of a basis in the space of such a representation has a natural interpretation in the language of Yangians, studied by M.Nazarov and V.Tarasov. Olshansky, Nazarov and MolevAlexander Molev
Alexander Ivanovich Molev is a Russian–Australian mathematician.He completed his Ph.D. in 1986 under the supervision of Alexandre Kirillov...
later discovered a generalization of this theory to other classical Lie algebra
Classical group
In mathematics, the classical Lie groups are four infinite families of Lie groups closely related to the symmetries of Euclidean spaces. Their finite analogues are the classical groups of Lie type...
s, based on the twisted Yangian.
Applications to physics
Yangian appears as a symmetry group in different models in physics. The most famous one is super-symmetric Yang-Mills field in four dimensions.Yangian also appears as a symmetry group of one dimensional exactly solvable models such as spin chains
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
, Hubbard model and in models of one dimensional relativistic quantum field theory.
Representation theory of Yangians
Irreducible finite-dimensional representations of Yangians were parametrized by Drinfeld in a way similar to the highest weight theory in the representation theory of semisimple Lie algebras. The role of the highest weight is played by a finite set of Drinfeld polynomials. Drinfeld also discovered a generalization of the classical Schur–Weyl dualitySchur–Weyl duality
Schur–Weyl duality is a mathematical theorem in representation theory that relates irreducible finite-dimensional representations of the general linear and symmetric groups...
between representations of general linear and symmetric group
Symmetric group
In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s that involves the Yangian of slN and the degenerate affine Hecke algebra (graded Hecke algebra of type A, in George Lusztig's terminology).
Representations of Yangians have been extensively studied, but the theory is still under active development.