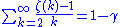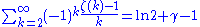Zeta constant
Encyclopedia
In mathematics
, a zeta constant is a number obtained by plugging an integer into the Riemann zeta function. This article provides a number of series identities for the zeta function for integer values.
, one has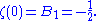
There is a pole at 1, so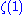
is not defined but the left and right limits are: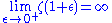
and
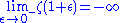
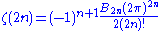
for
. The first few values are given by:
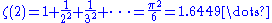
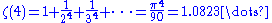
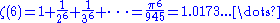
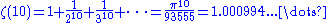
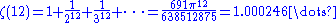
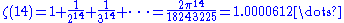
The relationship between zeta at the positive even integers and the Bernoulli numbers may be written as
where An and Bn are integers for all even n. These are given by the integer sequences and in OEIS. Some of these values are reproduced below:
If we let
be the coefficient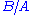 
as above,
then we find recursively,
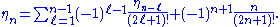
This recurrence relation may be derived from that for the Bernoulli number
s.
The even zeta constants have the generating function
:
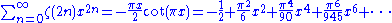
Since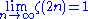
, the formula also shows that for 
:
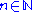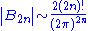as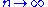 
where the symbol ~ means "asymptotic to" (see asymptotic notation).
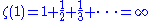(the harmonic series
);
(Apéry's constant
)
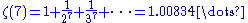
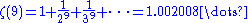
It is known that ζ(3) is irrational (Apéry's theorem) and that infinitely many of the numbers ζ(2n+1) (n ∈ N) are irrational. There are also results on the (ir)rationality of values of the Riemann zeta function at the elements of certain subsets of the positive odd integers; for example, at least one of ζ(5), ζ(7), ζ(9), or ζ(11) is irrational. This has significance for application to physics. Correlation functions
in antiferromagnetic xxx spin chain
can be expressed in terms of values of zeta at odd argumets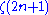
.
Most of the identities following below are provided by Simon Plouffe
. They are notable in that they converge quite rapidly, giving almost three digits of precision per iteration, and are thus useful for high-precision calculations.
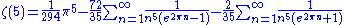
and
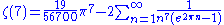
Note that the sum is in the form of the Lambert series.
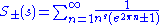
a series of relationships can be given in the form
where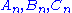
and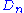 
are positive integers. Plouffe gives a table of values:
These integer constants may be expressed as sums over Bernoulli numbers, as given in (Vepstas, 2006) below.
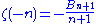
for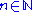
.
The so-called "trivial zeros" occur at the negative even integers:
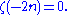
The first few values for negative odd integers are
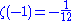
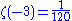
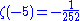
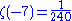
However, just like the Bernoulli numbers, these do not stay small for increasingly negative odd values. For details on the first value, see 1 + 2 + 3 + 4 + · · ·.
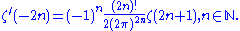
The first few values of which are
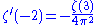
One also has
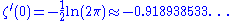
and
where
is the Glaisher-Kinkelin constant
.
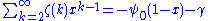
where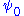
is the digamma function.
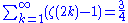
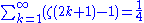
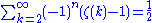
Series related to the Euler–Mascheroni constant
(denoted by γ) are
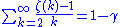
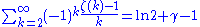
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a zeta constant is a number obtained by plugging an integer into the Riemann zeta function. This article provides a number of series identities for the zeta function for integer values.
The Riemann zeta function at 0 and 1
At zeroZero (complex analysis)
In complex analysis, a zero of a holomorphic function f is a complex number a such that f = 0.-Multiplicity of a zero:A complex number a is a simple zero of f, or a zero of multiplicity 1 of f, if f can be written asf=g\,where g is a holomorphic function g such that g is not zero.Generally, the...
, one has
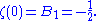
There is a pole at 1, so
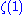is not defined but the left and right limits are: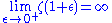and
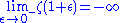
Even positive integers
For the even positive integers, one has the well-known relationship to the Bernoulli numbers, given by Euler: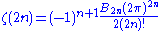for
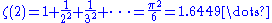
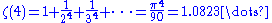
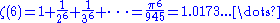
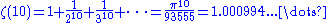
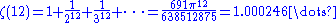
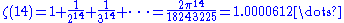
. The first few values are given by: The relationship between zeta at the positive even integers and the Bernoulli numbers may be written as
where An and Bn are integers for all even n. These are given by the integer sequences and in OEIS. Some of these values are reproduced below:
| 2n | A | B |
|---|---|---|
| 2 | 6 | 1 |
| 4 | 90 | 1 |
| 6 | 945 | 1 |
| 8 | 9450 | 1 |
| 10 | 93555 | 1 |
| 12 | 638512875 | 691 |
| 14 | 18243225 | 2 |
| 16 | 325641566250 | 3617 |
| 18 | 38979295480125 | 43867 |
| 20 | 1531329465290625 | 174611 |
| 22 | 13447856940643125 | 155366 |
| 24 | 201919571963756521875 | 236364091 |
| 26 | 11094481976030578125 | 1315862 |
| 28 | 564653660170076273671875 | 6785560294 |
| 30 | 5660878804669082674070015625 | 6892673020804 |
| 32 | 62490220571022341207266406250 | 7709321041217 |
| 34 | 12130454581433748587292890625 | 151628697551 |
If we let
be the coefficient as above,then we find recursively,
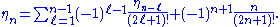
This recurrence relation may be derived from that for the Bernoulli number
Bernoulli number
In mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....
s.
The even zeta constants have the generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
:
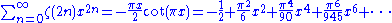
Since
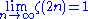, the formula also shows that for 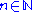: 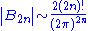as 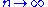where the symbol ~ means "asymptotic to" (see asymptotic notation).
Odd positive integers
For the first few odd natural numbers one has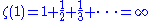 (the harmonic seriesHarmonic series (mathematics)
In mathematics, the harmonic series is the divergent infinite series:Its name derives from the concept of overtones, or harmonics in music: the wavelengths of the overtones of a vibrating string are 1/2, 1/3, 1/4, etc., of the string's fundamental wavelength...
);
(Apéry's constantApéry's constant
In mathematics, Apéry's constant is a number that occurs in a variety of situations. It arises naturally in a number of physical problems, including in the second- and third-order terms of the electron's gyromagnetic ratio using quantum electrodynamics...
)
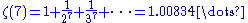
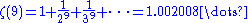
It is known that ζ(3) is irrational (Apéry's theorem) and that infinitely many of the numbers ζ(2n+1) (n ∈ N) are irrational. There are also results on the (ir)rationality of values of the Riemann zeta function at the elements of certain subsets of the positive odd integers; for example, at least one of ζ(5), ζ(7), ζ(9), or ζ(11) is irrational. This has significance for application to physics. Correlation functions
Correlation function (statistical mechanics)
In statistical mechanics, the correlation function is a measure of the order in a system, as characterized by a mathematical correlation function, and describes how microscopic variables at different positions are correlated....
in antiferromagnetic xxx spin chain
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
can be expressed in terms of values of zeta at odd argumets
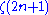.Most of the identities following below are provided by Simon Plouffe
Simon Plouffe
Simon Plouffe is a Quebec mathematician born on June 11, 1956 in Saint-Jovite, Quebec. He discovered the formula for the BBP algorithm which permits the computation of the nth binary digit of π, in 1995...
. They are notable in that they converge quite rapidly, giving almost three digits of precision per iteration, and are thus useful for high-precision calculations.
ζ(5)
Plouffe gives the identities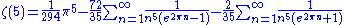and
ζ(7)
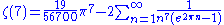
Note that the sum is in the form of the Lambert series.
ζ(2n+1)
By defining the quantities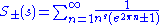a series of relationships can be given in the form
where
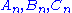and 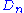are positive integers. Plouffe gives a table of values:| n | A | B | C | D |
|---|---|---|---|---|
| 3 | 180 | 7 | 360 | 0 |
| 5 | 1470 | 5 | 3024 | 84 |
| 7 | 56700 | 19 | 113400 | 0 |
| 9 | 18523890 | 625 | 37122624 | 74844 |
| 11 | 425675250 | 1453 | 851350500 | 0 |
| 13 | 257432175 | 89 | 514926720 | 62370 |
| 15 | 390769879500 | 13687 | 781539759000 | 0 |
| 17 | 1904417007743250 | 6758333 | 3808863131673600 | 29116187100 |
| 19 | 21438612514068750 | 7708537 | 42877225028137500 | 0 |
| 21 | 1881063815762259253125 | 68529640373 | 3762129424572110592000 | 1793047592085750 |
These integer constants may be expressed as sums over Bernoulli numbers, as given in (Vepstas, 2006) below.
Negative integers
In general, for negative integers, one has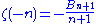for
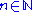.The so-called "trivial zeros" occur at the negative even integers:
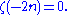
The first few values for negative odd integers are
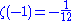
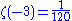
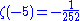
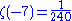
However, just like the Bernoulli numbers, these do not stay small for increasingly negative odd values. For details on the first value, see 1 + 2 + 3 + 4 + · · ·.
Derivatives
The derivative of the zeta function at the negative even integers is given by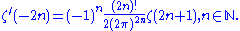The first few values of which are
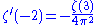
One also has
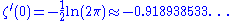
and
where
is the Glaisher-Kinkelin constantGlaisher-Kinkelin constant
In mathematics, the Glaisher–Kinkelin constant or Glaisher's constant, typically denoted A, is a mathematical constant, related to the K-function and the Barnes G-function. The constant appears in a number of sums and integrals, especially those involving Gamma functions and zeta functions...
.
Sum of zeta constants
The following sums can be derived from the generating function: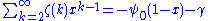where
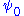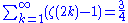
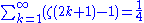
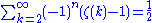
is the digamma function.Series related to the Euler–Mascheroni constant
Euler–Mascheroni constant
The Euler–Mascheroni constant is a mathematical constant recurring in analysis and number theory, usually denoted by the lowercase Greek letter ....
(denoted by γ) are